Кактус граф - Cactus graph

Кактусовый граф

В теория графов, а кактус (иногда называемый кактус) это связный граф в котором любые два простых циклы имеют не более одной общей вершины. Эквивалентно, это связный граф, в котором каждое ребро принадлежит не более чем одному простому циклу, или (для нетривиального кактуса), в котором каждый блок (максимальный подграф без вырезать вершину ) - ребро или цикл.

Характеристики

Кактусы бывают внешнепланарные графы. Каждый псевдодерево это кактус. Нетривиальный граф является кактусом тогда и только тогда, когда каждый блокировать является либо простой цикл или одиночный край.

Семейство графов, в котором каждый компонент это кактус это вниз закрыт под граф минор операции. Это семейство графов можно охарактеризовать одним запрещенный несовершеннолетний, четырехвершинник ромбовидный график формируется путем удаления края из полный график K₄.^[1]

Треугольный кактус

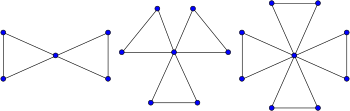
Графики дружбы кактусы треугольной формы

Треугольный кактус - это особый тип кактусового графа, каждый цикл которого имеет длину три. Например, графы дружбы, графы, образованные из набора треугольников, соединенных в одной общей вершине, являются треугольными кактусами. Треугольные кактусы не только графики кактусов, но и блочные графики.

Самый большой треугольный кактус в любом графе можно найти в полиномиальное время используя алгоритм для проблема четности матроидов. Поскольку треугольные графы кактусов планарные графы, самый большой треугольный кактус можно использовать в качестве приближения к самому большому плоскому подграфу, что является важной подзадачей в планаризация. Как алгоритм аппроксимации, этот метод имеет коэффициент аппроксимации 4/9, наиболее известная проблема максимального плоского подграфа.^[2]

Алгоритм поиска самого большого треугольного кактуса связан с теоремой Ловаса и Пламмера, которая характеризует количество треугольников в этом самом большом кактусе.^[3]Ловас и Пламмер рассматривают пары разбиений вершин и ребер данного графа на подмножества с тем свойством, что каждый треугольник графа либо имеет две вершины в одном классе вершинного разбиения, либо все три ребра в одном классе графа. краевая перегородка; они называют пару разделов с этим свойством действительный.Тогда количество треугольников в самом большом треугольном кактусе равно максимальному по парам допустимых разделов. ${ Displaystyle { mathcal {P}} = {V_ {1}, V_ {2}, dots, V_ {k} }}$ и ${ displaystyle { mathcal {Q}} = {E_ {1}, E_ {2}, dots, E_ {m} }}$ , из

{ displaystyle sum _ {я = 1} ^ {m} { frac {(u_ {i} -1)} {2}} + n-k,}

,

куда ${ displaystyle n}$ - количество вершин в данном графе и ${ displaystyle u_ {i}}$ это количество классов вершин, встречающихся в классе ребер ${ displaystyle E_ {i}}$ .

Недавно была доказана точная экстремальная оценка^[4] который показал, что при любом плоский график ${ displaystyle G}$ , всегда существует подграф кактуса ${ Displaystyle C substeq G}$ содержащий по крайней мере ${ displaystyle 1/6}$ доля треугольных граней ${ displaystyle G}$ . Этот результат подразумевает прямой анализ алгоритма приближения 4/9 для задачи о максимальном плоском подграфе без использования приведенной выше формулы min-max.

Гипотеза Розы

Важная гипотеза, связанная с треугольным кактусом, - это Гипотеза Розы, названный в честь Александр Роза, который говорит, что все треугольные кактусы изящный или почти изящный.^[5] Точнее

Все треугольные кактусы с t 0, 1 mod 4 изящны, а с t 2, 3 mod 4 - почти изящными.

Алгоритмы и приложения

Немного проблемы с расположением объекта которые NP-жесткий для общих графиков, а также некоторые другие проблемы с графами могут быть решены в полиномиальное время для кактусов.^[6]^[7]

Поскольку кактусы - частные случаи внешнепланарные графы, номер комбинаторная оптимизация задачи на графах могут быть решены для них в полиномиальное время.^[8]

Кактусы представляют электрические схемы обладающие полезными свойствами. Раннее применение кактусов было связано с представлением операционных усилителей.^[9]^[10]^[11]

Кактусы также недавно использовались в сравнительная геномика как способ представления взаимосвязи между различными геномами или частями геномов.^[12]

Если кактус связан, и каждая его вершина принадлежит не более чем двум блокам, то он называется Рождественский кактус. Каждый многогранный граф имеет подграф рождественского кактуса, который включает в себя все его вершины, факт, который играет важную роль в доказательстве Лейтон и Мойтра (2010) что каждый многогранный граф имеет жадное вложение в Евклидова плоскость, присвоение координат вершинам, для которых жадная пересылка успешно маршрутизирует сообщения между всеми парами вершин.^[13]

В топологическая теория графов, графы, клеточные вложения все планарный являются в точности подсемейством графов кактусов с дополнительным свойством, что каждая вершина принадлежит не более чем одному циклу. В этих графах есть два запрещенных минора, ромбовидный граф и пятивершинный граф дружбы.^[14]

История

Кактусы впервые были изучены под именем Деревья Хусими, дарованный им Фрэнк Харари и Джордж Юджин Уленбек в честь предыдущей работы над этими графиками Коди Хусими.^[15]^[16] В той же статье Харари – Уленбека зарезервировано название «кактус» для графов этого типа, в которых каждый цикл представляет собой треугольник, но теперь стандартное разрешение циклов любой длины.

Между тем имя Дерево Хусими обычно относятся к графам, в которых каждый блокировать это полный график (эквивалентно графам пересечений блоков в каком-то другом графе). Это употребление имело мало общего с работой Хусими, и более подходящий термин блочный граф теперь используется для этого семейства; однако из-за этой двусмысленности эта фраза стала реже использоваться для обозначения графов кактусов.^[17]

внешняя ссылка

Применение графиков кактусов в анализе и проектировании электронных схем

[1] Эль-Маллах, Эхаб; Колборн, Чарльз Дж. (1988), "Сложность некоторых задач удаления ребер", Транзакции IEEE в схемах и системах, 35 (3): 354–362, Дои:10.1109/31.1748

[2] Кэлинеску, Груя; Фернандес, Кристина Дж. Финклер, Ульрих; Карлофф, Ховард (2002), "Алгоритм лучшего приближения для поиска плоских подграфов", Журнал алгоритмов, 2, 27 (2): 269–302, CiteSeerX 10.1.1.47.4731, Дои:10.1006 / jagm.1997.0920, S2CID 8329680

[3] Ловас, Л.; Пламмер, доктор медицины (2009), Теория соответствия, Издательство AMS Chelsea Publishing Series, ISBN 9780821847596

[4] Чалермсук, Париня; Шмид, Андреас; Uniyal, Sumedha (2019), "Жесткая экстремальная граница числа кактусов Ловаша в плоских графах", CoRR, абс / 1804.03485, arXiv:1804.03485, Дои:10.4230 / LIPIcs.STACS.2019.19, S2CID 4751972

[Rosa1988-5] Роза, А. (1988), "Циклические тройные системы Штейнера и маркировка треугольных кактусов", Scientia, 1: 87–95.

[6] Бен-Моше, Вооз; Бхаттачарья, Бинай; Ши, Цяошэн (2005), «Эффективные алгоритмы для взвешенной задачи с двумя центрами в кактусовом графе», Алгоритмы и вычисления, 16-я Int. Symp., ISAAC 2005, Конспект лекций по информатике, 3827, Springer-Verlag, стр. 693–703, Дои:10.1007/11602613_70, ISBN 978-3-540-30935-2

[7] Змазек, Блаз; Зеровник, Янез (2005), "Оценка трафика на взвешенных сетях кактусов за линейное время", Девятая Международная конференция по визуализации информации (IV'05), стр. 536–541, Дои:10.1109 / IV.2005.48, ISBN 978-0-7695-2397-2, S2CID 15963409

[8] Корнеенко, Н. М. (1994), "Комбинаторные алгоритмы на одном классе графов", Дискретная прикладная математика, 54 (2–3): 215–217, Дои:10.1016 / 0166-218X (94) 90022-1. Переведено с Извещения АН БССР, сер. Физ.-мат. Sci., (1984) нет. 3. С. 109-111. (на русском)

[9] Ниси, Тецуо; Чуа, Леон О. (1986), "Топологическое доказательство теоремы Нильсена-Вилсона", Транзакции IEEE в схемах и системах, 33 (4): 398–405, Дои:10.1109 / TCS.1986.1085935

[10] Ниси, Тецуо; Чуа, Леон О. (1986), «Единственность решения для нелинейных резистивных цепей, содержащих CCCS или VCVS, управляющие коэффициенты которых конечны», Транзакции IEEE в схемах и системах, 33 (4): 381–397, Дои:10.1109 / TCS.1986.1085934

[11] Ниси, Тецуо (1991), "О числе решений одного класса нелинейных резистивных цепей", Материалы Международного симпозиума IEEE по схемам и системам, Сингапур, стр. 766–769

[12] Патен, Бенедикт; Диханс, Марк; Эрл, Дент; Сент-Джон, Джон; Ма, Цзянь; Су, Бернард; Хаусслер, Дэвид (2010), «Графики кактусов для сравнения генома», Исследования в области вычислительной молекулярной биологии, Конспект лекций по информатике, 6044, стр.410–425, Дои:10.1007/978-3-642-12683-3_27, ISBN 978-3-642-12682-6

[13] Лейтон, Том; Мойтра, Анкур (2010), «Некоторые результаты о жадных вложениях в метрические пространства» (PDF), Дискретная и вычислительная геометрия, 44 (3): 686–705, Дои:10.1007 / s00454-009-9227-6, S2CID 11186402.

[14] Nordhaus, E. A .; Ringeisen, R.D .; Стюарт, Б. М .; Уайт, А. Т. (1972), "Теорема типа Куратовского для максимального рода графа", Журнал комбинаторной теории, Серия B, 12 (3): 260–267, Дои:10.1016/0095-8956(72)90040-8, МИСТЕР 0299523

[15] Харари, Фрэнк; Уленбек, Джордж Э. (1953), «О числе деревьев Хусими, I», Труды Национальной академии наук, 39 (4): 315–322, Дои:10.1073 / pnas.39.4.315, МИСТЕР 0053893, ЧВК 1063779, PMID 16589268

[16] Хусими, Коди (1950), "Заметка о теории кластерных интегралов Майерса", Журнал химической физики, 18 (5): 682–684, Дои:10.1063/1.1747725, МИСТЕР 0038903

[17] См., Например, МИСТЕР0659742, обзор Роберта Э. Джемисона в 1983 году статьи, в которой используется другое определение, в котором двусмысленность объясняется ошибкой в книге автора Мехди Бехзад и Гэри Чартранд.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]