И – или дерево - And–or tree - Wikipedia
An и – или дерево это графическое представление сокращения проблемы (или цели) союзы и дизъюнкции подзадач (или подзадач).
Пример
И / или дерево:
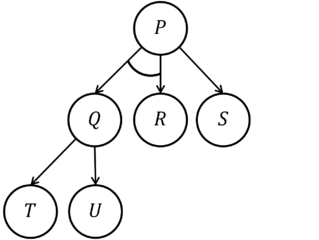
представляет пространство поиска для решения задачи P, используя методы приведения к цели:
- P, если Q и R
- P, если S
- Q, если T
- Q, если U
Определения
Учитывая исходную задачу P0 и набор методов решения задач в виде:
- P, если P1 и… и Pп
связанное и / или дерево представляет собой набор помеченных узлов, таких что:
- Корень дерева - это узел, помеченный P0.
- Для каждого узла N, помеченного проблемой или подзадачей P, и для каждого метода формы P, если P1 и… и Pп, существует набор дочерних узлов N1,…, Nп узла N, так что каждый узел Nя обозначается Pя. Узлы соединены дугой, чтобы отличить их от потомков N, которые могут быть связаны с другими методами.
Узел N, помеченный проблемой P, является успешным узлом, если существует метод формы P, если ничего нет (т.е. P является «фактом»). Узел считается узлом отказа, если нет метода решения P.
Если все дочерние узлы узла N, соединенные одной дугой, являются узлами успеха, тогда узел N также является узлом успеха. В противном случае узел является отказавшим узлом.
Стратегии поиска
Дерево и / или определяет только область поиска для решения проблемы. Разные стратегии поиска для поиска места возможны. К ним относятся поиск в дереве сначала в глубину, в ширину или в первую очередь с использованием некоторой меры желательности решений. Стратегия поиска может быть последовательной, поиск или создание одного узла за раз, или параллельной, поиск или создание нескольких узлов параллельно.
Связь с логическим программированием
Методы, используемые для генерации и / или деревьев, являются пропозициональными. логические программы (без переменных). В случае логических программ, содержащих переменные, решения совместных подзадач должны быть совместимыми. С учетом этого усложнения стратегии последовательного и параллельного поиска и / или деревьев обеспечивают вычислительную модель для выполнения логических программ.
Отношения с играми для двух игроков
И – или деревья могут также использоваться для представления пространств поиска для игр для двух человек. Корневой узел такого дерева представляет проблему выигрыша одного из игроков в игре, начиная с начального состояния игры. Для данного узла N, обозначенного проблемой P игрока, выигрывающего игру в конкретном состоянии игры, существует единственный набор совместных дочерних узлов, соответствующий всем ответным ходам оппонентов. Для каждого из этих дочерних узлов существует набор несоединенных дочерних узлов, соответствующих всем защитным ходам игрока.
Для решения игровых деревьев с помощью поиск номера проверки семейства алгоритмов, игровые деревья должны быть отображены на и / или деревья. MAX-узлы (то есть максимальное перемещение игрока) представлены как узлы OR, MIN-узлы отображаются на узлы AND. Отображение возможно, когда поиск выполняется только с бинарной целью, обычно это «игрок, который переместится, выигрывает игру».
Библиография
- Люгер, Джордж Ф .; Стаблфилд, Уильям А. (1993). Искусственный интеллект: структуры и стратегии для решения сложных задач (2-е изд.). Бенджамин / Каммингс. ISBN 978-0-8053-4785-2. Получено 28 февраля 2013.
- Нильссон, Нильс Дж. (1998). Искусственный интеллект: новый синтез. Морган Кауфманн. ISBN 978-1-55860-467-4. Получено 28 февраля 2013.
