Угловой диаметр - Angular diameter - Wikipedia

В угловой диаметр, угловой размер, кажущийся диаметр, или же очевидный размер угловое измерение, описывающее, насколько велик сфера или же круг появляется с данной точки зрения. в видение науки, это называется угол обзора, И в оптика, это угловая апертура (из линза ). В качестве альтернативы угловой диаметр можно рассматривать как угол, на который глаз или камера должны повернуться, чтобы смотреть с одной стороны видимого круга на противоположную. Угловой радиус равняется половине углового диаметра.

Формула

Схема для формулы углового диаметра

Угловой диаметр круг плоскость которого перпендикулярна вектору смещения между точкой обзора и центром указанного круга, можно рассчитать по формуле^[1]

{ displaystyle delta = 2 arctan left ({ frac {d} {2D}} right),}

в котором ${ displaystyle delta}$ угловой диаметр, а ${ displaystyle d}$ фактический диаметр объекта, и ${ displaystyle D}$ расстояние до объекта. Когда ${ displaystyle D gg d}$ , у нас есть ${ displaystyle delta приблизительно d / D}$ , а полученный результат находится в радианы.

Для сферического объекта, действительный диаметр равен ${ displaystyle d _ { mathrm {act}},}$ и где ${ displaystyle D}$ это расстояние до центр сферы угловой диаметр можно найти по формуле

{ displaystyle delta = 2 arcsin left ({ frac {d _ { mathrm {act}}} {2D}} right)}

Различие связано с тем, что видимые края сферы - это точки касания, которые находятся ближе к наблюдателю, чем центр сферы. Для практического использования различие важно только для сферических объектов, которые находятся относительно близко, поскольку малоугловое приближение держится для ${ Displaystyle х ll 1}$ :^[2]

{ Displaystyle arcsin x приблизительно arctan x приблизительно x}

.

Оценка углового диаметра с помощью руки

Приблизительные углы 10 °, 20 °, 5 ° и 1 ° для вытянутой руки.

Оценки углового диаметра можно получить, держа руку под прямым углом к полностью выдвинутая рука, как показано на рисунке.^[3]^[4]^[5]

Использование в астрономии

Угловой диаметр: угол, образуемый объектом.

В астрономия, размеры небесные объекты часто даются с точки зрения их углового диаметра, как видно из земной шар, а не их реальные размеры. Поскольку эти угловые диаметры обычно малы, их принято представлять в угловые секунды (″). Угловая секунда равна 1/3600 доли единицы степень (1 °), а радиан - 180 / ${ displaystyle pi}$ градусов. Таким образом, один радиан равен 3600 × 180 / ${ displaystyle pi}$ угловых секунд, что составляет около 206 265 угловых секунд (1 рад ≈ 206 264,806247 дюймов). Следовательно, угловой диаметр объекта с физическим диаметром d На расстоянии D, выраженное в угловых секундах, определяется как:^[6]

{ displaystyle delta = 206 265 ~ (d / D) ~ mathrm {arcseconds}}

.

Эти объекты имеют угловой диаметр 1 дюйм:

объект диаметром 1 см на удалении 2,06 км
объект диаметром 725,27 км на расстоянии 1 астрономическая единица (Австралия)
объект диаметром 45 866 916 км на 1 световой год
объект диаметром 1 а.е. (149 597 871 км) на расстоянии 1 парсек (ПК)

Таким образом, угловой диаметр Орбита Земли вокруг солнце если смотреть с расстояния 1 пк, это 2 дюйма, так как 1 а.е. - это средний радиус орбиты Земли.

Угловой диаметр Солнца с расстояния один световой год, составляет 0,03 дюйма, а земной шар 0,0003 ″. Угловой диаметр 0,03 дюйма Солнца, указанный выше, примерно такой же, как у человеческого тела на расстоянии диаметра Земли.

В этой таблице приведены угловые размеры заслуживающих внимания небесные тела как видно с Земли:

Небесное тело	Угловой диаметр или размер	Относительный размер
Галактика Андромеды	3 ° 10 ′ на 1 °	Примерно в шесть раз больше Солнца или Луны. Только гораздо меньшее ядро видно без фотография с длинной выдержкой.
солнце	31′27″ – 32′32″	30–31 раз больше максимального значения для Венеры (оранжевая полоса внизу) / 1887–1952 ″
Луна	29′20″ – 34′6″	28–32,5 раза больше максимального значения для Венеры (оранжевая полоса внизу) / 1760–2046 ″
Туманность спираль	примерно 16 'на 28'
Шпиль в Туманность Орла	4′40″	длина 280 ″
Венера	9.7″ – 1′6″
Юпитер	29.8″ – 50.1″
Сатурн	14.5″ – 20.1″
Марс	3.5″ – 25.1″
Меркурий	4.5″ – 13.0″
Уран	3.3″ – 4.1″
Нептун	2.2″ – 2.4″
Церера	0.33″ – 0.84″
Веста	0.20″ – 0.64″
Плутон	0.06″ – 0.11″
Р Дорадус	0.052″ – 0.062″
Бетельгейзе	0.049″ – 0.060″
Эрис	0.034″ – 0.089″
Alphard	0.00909″
Альфа Центавра A	0.007″
Канопус	0.006″
Сириус	0.005936″
Альтаир	0.003″
Денеб	0.002″
Проксима Центавра	0.001″
Альнитак	0.0005″
Горизонт событий черной дыры M87 * в центре галактики M87, изображенной Телескоп горизонта событий в 2019 году.	0.000025″ (2.5×10⁻⁵)
Звезда как Альнитак на расстоянии, где Космический телескоп Хаббла просто смог бы это увидеть^[7]	6×10⁻¹⁰ arcsec

Сравнение углового диаметра Солнца, Луны и планет. Чтобы получить точное представление о размерах, просматривайте изображение с расстояния, в 103 раза превышающего ширину «Луны: макс.». круг. Например, если на вашем мониторе ширина этого круга составляет 5 см, просматривайте его с расстояния 5,15 м.

На этой фотографии сравниваются видимые размеры Юпитер и его четыре Галилеевы луны (Каллисто максимум удлинение ) с кажущимся диаметром полнолуние во время их соединение 10 апреля 2017 г.

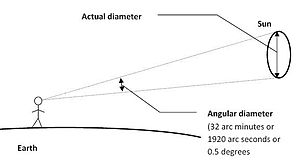
Таблица показывает, что угловой диаметр Солнца, если смотреть с Земли, составляет примерно 32 '(1920 ″ или 0,53 °), как показано выше.

Таким образом, угловой диаметр Солнца примерно в 250 000 раз больше, чем у Солнца. Сириус. (Диаметр Сириуса вдвое больше, а расстояние до него в 500000 раз больше; до Солнца 10¹⁰ раз ярче, что соответствует соотношению угловых диаметров 10⁵, поэтому Сириус примерно в 6 раз ярче на единицу телесный угол.)

Угловой диаметр Солнца также примерно в 250 000 раз больше, чем у Солнца. Альфа Центавра A (у него примерно такой же диаметр, а расстояние в 250 000 раз больше; Солнце имеет размер 4 × 10¹⁰ раз ярче, что соответствует соотношению угловых диаметров 200000, поэтому Альфа Центавра A немного ярче на единицу телесного угла).

Угловой диаметр Солнца примерно такой же, как у Солнца. Луна. (Диаметр Солнца в 400 раз больше, равно как и расстояние до него; Солнце в 200000-500000 раз ярче полной Луны (цифры различаются), что соответствует отношению углового диаметра от 450 до 700, то есть небесное тело с диаметром 2,5–4 ″ и такой же яркости на единицу телесного угла будет иметь такую же яркость, как полная Луна.)

Хотя Плутон физически больше Цереры, если смотреть с Земли (например, через Космический телескоп Хаббла ) Церера имеет гораздо больший кажущийся размер.

Угловые размеры, измеряемые в градусах, полезны для больших участков неба. (Например, три звезды Ремень покрывают примерно 4,5 ° углового размера.) Однако для измерения угловых размеров галактик, туманностей или других объектов Земли требуются гораздо более точные единицы измерения. ночное небо.

Таким образом, степени подразделяются следующим образом:

360 градусы (°) по полному кругу
60 угловые минуты (′) В одной степени
60 угловые секунды (″) За одну угловую минуту

Чтобы представить это в перспективе, полнолуние с Земли примерно¹⁄₂°, или 30 '(или 1800 ″). Движение Луны по небу можно измерить по угловому размеру: примерно 15 ° каждый час или 15 дюймов в секунду. Линия длиной в одну милю, нарисованная на лице Луны, будет казаться с Земли примерно 1 дюйм в длину.

Минимальное, среднее и максимальное расстояния от Луны до Земли с ее угловым диаметром, если смотреть с поверхности Земли, в масштабе

В астрономии обычно трудно напрямую измерить расстояние до объекта, но объект может иметь известный физический размер (возможно, он похож на более близкий объект с известным расстоянием) и измеримый угловой диаметр. В этом случае формулу углового диаметра можно обратить, чтобы получить расстояние по угловому диаметру на далекие объекты как

{ Displaystyle д эквив 2D загар влево ({ гидроразрыва { дельта} {2}} вправо)}

.

В неевклидовом пространстве, таком как наша расширяющаяся Вселенная, расстояние по угловому диаметру является лишь одним из нескольких определений расстояния, так что могут быть разные «расстояния» до одного и того же объекта. Видеть Меры расстояния (космология).

Некруглые объекты

Много объекты глубокого космоса Такие как галактики и туманности кажутся некруглыми и, таким образом, обычно имеют две меры диаметра: большую ось и малую ось. Например, Малое Магелланово Облако имеет видимый видимый диаметр 5 ° 20 ′ × 3 ° 5 ′.

Дефект освещения

Дефект освещения - это максимальная угловая ширина неосвещенной части небесного тела, видимой данным наблюдателем. Например, если объект имеет диаметр 40 дюймов по дуге и освещен на 75%, дефект освещения составляет 10 дюймов.

Смотрите также

внешняя ссылка

[1] Это можно вывести, используя формулу для длины шнура, найденную в «Круговой сегмент». В архиве из оригинала 21.12.2014. Получено 2015-01-23.

[2] «Ряд Тейлора для функционера арктана» (PDF). Архивировано из оригинал (PDF) на 2015-02-18. Получено 2015-01-23.

[3] «Системы координат». Архивировано из оригинал на 2015-01-21. Получено 2015-01-21.

[4] «Фотосъемка спутников». 8 июня 2013 г. В архиве из оригинала от 21 января 2015 г.

[5] Викиверситет: Физико-астрономические лаборатории / Угловой размер

[6] Майкл А. Сидс; Дана Э. Бакман (2010). Звезды и галактики (7-е изд.). Брукс Коул. п. 39. ISBN 978-0-538-73317-5.

[7] Угловой диаметр в 800 000 раз меньше, чем у Альнитака, если смотреть с Земли. Альнитак - голубая звезда, поэтому она излучает много света для своего размера. Если бы он находился в 800 000 раз дальше, то имел бы звездную величину 31,5, на пределе того, что видит Хаббл.

[1]

[2]

[3]

[4]

[5]

[6]

[7]