Архимедов граф - Archimedean graph
в математический поле теория графов, Архимедов граф это график образующий скелет одного из Архимедовы тела. Существует 13 графов Архимеда, и все они обычный, многогранник (и поэтому по необходимости также 3-вершинно-связанный планарные графы ), а также Гамильтоновы графы.[1]
Наряду с 13, множество бесконечных призматические графики и графики антипризмы также можно рассматривать архимедовы графы.[2]
| Имя | График | Степень | Края | Вершины | Заказ |
|---|---|---|---|---|---|
| усеченный тетраэдрический граф | 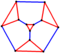 | 3 | 18 | 12 | 24 |
| кубооктаэдрический граф |  | 4 | 24 | 12 | 48 |
| усеченный кубический граф |  | 3 | 36 | 24 | 48 |
| усеченный октаэдрический граф | 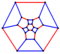 | 3 | 36 | 24 | 48 |
| ромбокубооктаэдрический граф |  | 4 | 48 | 24 | 48 |
| усеченный кубооктаэдрический граф (большой ромбокубооктаэдр) |  | 3 | 72 | 48 | 48 |
| курносый кубический граф |  | 5 | 60 | 24 | 24 |
| икосододекаэдрический граф |  | 4 | 60 | 30 | 120 |
| усеченный додекаэдрический граф |  | 3 | 90 | 60 | 120 |
| усеченный икосаэдрический граф | 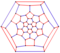 | 3 | 90 | 60 | 120 |
| ромбикосододекаэдрический граф |  | 4 | 120 | 60 | 120 |
| усеченный икосододекаэдрический граф (большой ромбоикосододекаэдр) |  | 3 | 180 | 120 | 120 |
| курносый додекаэдрический граф |  | 5 | 150 | 60 | 60 |
Смотрите также
Рекомендации
- Рид, Р. К. и Уилсон, Р. Дж. Атлас графиков, Oxford, England: Oxford University Press, перепечатка 2004 г., глава 6 специальные графики С. 261, 267-269.
внешняя ссылка
| Этот комбинаторика -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
