Центр перкуссии - Center of percussion

В центр перкуссии точка на протяженном массивном объекте, прикрепленном к оси, где перпендикуляр удар не вызовет реактивного удара на оси поворота. Поступательные и вращательные движения отменяются в точке поворота, когда импульсный удар наносится по центру удара. Центр удара часто обсуждается в контексте летучей мыши, ракетка, дверь, меч или другой протяженный объект, удерживаемый за один конец.

Эта же точка называется центр колебаний для объекта, подвешенного к оси как маятник Это означает, что простой маятник, вся масса которого сосредоточена в этой точке, будет иметь тот же период колебаний, что и составной маятник.

В спорте центр удара битой или ракеткой относится к так называемому "сладкое пятно «, но последнее также связано с колебательным изгибом объекта.

Объяснение

Последствия удара по подвесной балке. CP - это центр удара, а CM - центр масс луча.

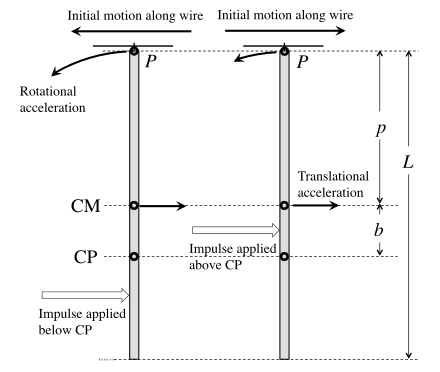
Представьте жесткую балку, подвешенную к проволоке с помощью приспособления, которое может свободно скользить по проволоке в точке P, как показано на рисунке. Импульсный удар наносится слева. Если он ниже центр массы (CM) это заставит луч вращаться против часовой стрелки вокруг CM, а также заставит CM двигаться вправо. Центр перкуссии (ЦП) находится ниже ЦМ. Если удар падает выше CP, поступательное движение вправо будет больше, чем вращательное движение влево в точке P, в результате чего чистое начальное движение приспособления будет направлено вправо. Если удар падает ниже CP, произойдет обратное: вращательное движение в точке P будет больше, чем поступательное движение, и приспособление сначала переместится влево. Только если удар падает точно на CP, два компонента движения компенсируются, чтобы произвести нулевое начальное движение в точке P.

Когда скользящее приспособление заменяется шарниром, который не может перемещаться влево или вправо, импульсный удар в любом месте, кроме CP, приводит к возникновению начальной реактивной силы на оси.

Расчет центра удара

Для свободной жесткой балки импульс ${\displaystyle Fdt}$ применяется в прямой угол На расстоянии ${\displaystyle b}$ от центр массы (CM) приведет к изменению скорости CM ${\displaystyle dv_{cm}}$ согласно соотношению:

${\displaystyle F=M{\frac {dv_{cm}}{dt}},}$

куда ${\displaystyle M}$ - масса балки. Точно так же крутящий момент о СМ изменим угловая скорость ${\displaystyle \omega }$ в соответствии с:

${\displaystyle Fb=I{\frac {d\omega }{dt}},}$

куда ${\displaystyle I}$ это момент инерции вокруг СМ.

Для любой точки P расстояние ${\displaystyle p}$ на противоположной стороне ЦМ от точки удара изменение скорости точки P равно

${\displaystyle dv_{net}=dv_{cm}-pd\omega \,}$

куда ${\displaystyle p}$ расстояние P от CM. Следовательно, ускорение в точке P из-за импульсного удара равно:

${\displaystyle {\frac {dv_{net}}{dt}}=\left({\frac {1}{M}}-{\frac {pb}{I}}\right)F.}$

Когда это ускорение равно нулю, ${\displaystyle b}$ определяет центр перкуссии. Следовательно, расстояние CP, ${\displaystyle b}$, из КМ, определяется выражением

${\displaystyle b={\frac {I}{pM}}.}$

Обратите внимание, что P, ось вращения, не обязательно должна быть на конце балки, но может быть выбрана на любом расстоянии. ${\displaystyle p}$.

Длина ${\displaystyle b+p}$ также определяет центр колебаний из физический маятник, то есть положение массы простого маятника, имеющего тот же период, что и у физического маятника.^[1]

Центр удара равномерного луча

Для частного случая балки равномерной плотности длины ${\displaystyle L}$, момент инерции вокруг ЦМ равен:

${\displaystyle I={\frac {1}{12}}ML^{2}}$ (видеть момент инерции для доказательства),

и для вращения вокруг оси в конце,

${\displaystyle p=L/2}$.

Это ведет к:

${\displaystyle b={\frac {L^{2}}{12p}}={\frac {1}{6}}L}$.

Отсюда следует, что КП составляет 2/3 длины однородного пучка. ${\displaystyle L}$ с повернутого конца.

Некоторые приложения

Например, качающаяся дверь, которая останавливается дверным ограничителем, расположенным на 2/3 ширины двери, будет выполнять эту работу с минимальным встряхиванием двери, потому что откидной конец не подвергается действию чистой реактивной силы. (Эта точка также является узлом второй колебательной гармоники, что также минимизирует вибрацию.)

В сладкое пятно на бейсбол летучая мышь обычно определяется как точка, в которой удар чувствует лучше всего к тесту. Центр удара определяет место, где, если летучая мышь ударяет по мячу, а руки отбивающего находятся в точке поворота, отбивающий не чувствует внезапной силы реакции. Однако, поскольку летучая мышь не является жестким объектом, вибрации от удара также играют роль. Кроме того, точка поворота качелей не может находиться в том месте, где находятся руки отбивающего. Исследования показали, что доминирующий физический механизм определения зоны наилучшего восприятия возникает из расположения узлов в колебательных режимах летучей мыши, а не из расположения центра удара.^[2]

Концепция центра перкуссии может быть применена к мечи. Это гибкие объекты, поэтому «золотая середина» для такого режущего оружия зависит не только от центра удара, но также от характеристик изгиба и вибрации.^[3][4]

Рекомендации

1. Дэниел А. Рассел (16 июня 2005 г.). «Что такое КС и какое это имеет значение?». Физика и акустика бейсбольных и софтбольных бит. Государственный университет Пенсильвании. Архивировано из оригинал 5 апреля 2009 г.. Получено 24 мая, 2012.
2. Род Кросс (2004). «Центр ударных ручных инструментов» (PDF ). Американский журнал физики. 72 (5): 622–630. Bibcode:2004AmJPh..72..622C. Дои:10.1119/1.1634965.
3. Джордж Тернер (1999). «Движения и удары меча: исследование и анализ». Ассоциация боевых искусств эпохи Возрождения. Получено 24 мая, 2012.
4. Гейсслер, Роберт (2014). «О динамике мечей». HROARR. Получено 18 января, 2015.