Центрированное дерево - Centered tree
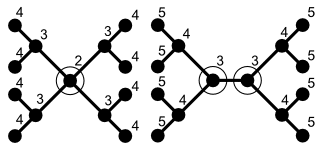
Слева центрированное дерево, справа двухцентровое. Цифры показывают эксцентриситет каждого узла.
В дискретной математике центрированное дерево это дерево только с одним центр, а двухцентровое дерево дерево с двумя центрами.
Для данного графа эксцентриситет вершины v определяется как наибольший расстояние из v в любую другую вершину. А центр графа - это вершина с минимальным эксцентриситетом. Граф может иметь произвольное количество центров. Однако, Иордания (1869) доказал, что для деревьев есть только две возможности:
- У дерева ровно один центр (центрированные деревья).
- У дерева ровно два центра (двухцентровые деревья). В этом случае два центра смежны.
Доказательство этого факта дает, например, Кнут.[1]
Примечания
Рекомендации
- Иордания, Камилла (1869). "Sur les Assemblages de lignes". Журнал für die reine und angewandte Mathematik (На французском). 70 (2): 185–190.
- Кнут, Дональд Э. (1997). Искусство программирования, Том 1: Основные алгоритмы (3-е изд.). Эддисон-Уэсли Профессионал. ISBN 0-201-89683-4.
внешняя ссылка
- Вайсштейн, Эрик В. «Двухцентровое дерево». MathWorld.
- Вайсштейн, Эрик В. "Центрированное дерево". MathWorld.
| Этот связанный с топологией статья - это заглушка. Вы можете помочь Википедии расширяя это. |
