Проблема обедающих криптографов - Dining cryptographers problem

В криптографии проблема обедающих криптографов изучает, как выполнять безопасные многосторонние вычисления функции логического ИЛИ. Дэвид Чаум впервые предложил эту проблему в начале 1980-х годов и использовал ее в качестве наглядного примера, чтобы показать, что можно отправлять анонимные сообщения с безусловным отсутствием отслеживания отправителя и получателя. Анонимные сети связи, основанные на этой проблеме, часто называют DC-сети (где DC означает «обедающие криптографы»).^[1]

Несмотря на слово обедатьпроблема обедающих криптографов не связана с проблема обедающих философов.

Описание

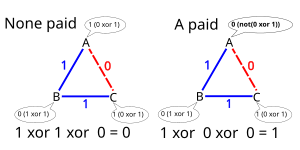
Обеденные криптографы проблема иллюстрации

Три криптографа собираются за столом на обед. Официант сообщает им, что еда была оплачена кем-то, кто мог быть одним из криптографов или Национальное Агенство Безопасности (АНБ). Криптографы уважают право друг друга на анонимный платеж, но хотят выяснить, заплатило ли АНБ. Поэтому они решили выполнить двухэтапный протокол.

На первом этапе каждые два криптографа устанавливают общий однобитовый секрет, например, бросая монету за меню, так что только два криптографа видят результат по очереди для каждых двух криптографов. Предположим, например, что после подбрасывания монеты криптограф A и B разделяют секретный бит ${displaystyle 1}$ , A и C делятся ${displaystyle 0}$ , а B и C разделяют ${displaystyle 1}$ .

На втором этапе каждый криптограф публично объявляет бит, а именно:

если они не заплатили за еду, Эксклюзивный или (XOR) двух общих битов, которые они удерживают со своими двумя соседями,
если они действительно заплатили за еду, противоположность тому XOR.

Предположим, никто из криптографов не заплатил, тогда А объявляет ${displaystyle 1oplus 0 = 1}$ , B объявляет ${displaystyle 1oplus 1 = 0}$ , а C объявляет ${displaystyle 0oplus 1 = 1}$ . С другой стороны, если A заплатила, она объявляет ${displaystyle lnot (1oplus 0) = 0}$ .

Три публичных объявления вместе дают ответ на их вопрос. Один просто вычисляет XOR трех объявленных битов. Если результат равен 0, это означает, что ни один из криптографов не заплатил (поэтому АНБ должно было оплатить счет). В противном случае один из криптографов заплатил, но их личность осталась неизвестной другим криптографам.

Дэвид Чаум ввел термин сеть обеденных криптографов, или DC-net для этого протокола.

Ограничения

Протокол DC-net прост и элегантен. Однако он имеет несколько ограничений, некоторые решения которых были изучены в ходе последующих исследований (см. Раздел «Ссылки» ниже).

Столкновение: Если за обед заплатили два криптографа, их сообщения будут отменять друг друга, и окончательный результат XOR будет ${displaystyle 0}$ . Это называется коллизией и позволяет только одному участнику передавать одновременно с использованием этого протокола. В более общем случае коллизия происходит, пока любое четное число участников отправляет сообщения.

Нарушение: Любой злонамеренный криптограф, который не хочет, чтобы группа успешно взаимодействовала, может заблокировать протокол, так что окончательный результат XOR станет бесполезным, просто отправив случайные биты вместо правильного результата XOR. Эта проблема возникает из-за того, что исходный протокол был разработан без использования каких-либо открытый ключ технологии и не имеет надежных механизмов, чтобы проверить, честно ли участники следуют протоколу.^[2]

Сложность: Протокол требует попарно общих секретных ключей между участниками, что может быть проблематичным, если участников много. Кроме того, хотя протокол DC-net является «безусловно безопасным», на самом деле он зависит от предположения, что «безусловно безопасные» каналы уже существуют между парами участников, чего нелегко достичь на практике.

Связанный анонимная сеть вето алгоритм вычисляет логическое ИЛИ для входов нескольких пользователей, а не логическое ИЛИ, как в DC-сетях, что может быть полезно в приложениях, для которых естественно подходит операция объединения логического ИЛИ.

История

Дэвид Чаум Впервые задумался об этой проблеме в начале 1980-х гг. Его первая публикация, в которой излагаются основные идеи.^[3] Журнальная версия появилась в самом первом выпуске Journal of Cryptology.^[4]

Обобщения

DC-сети легко обобщаются для обеспечения передачи более одного бита за раунд для групп, состоящих из более чем трех участников, и для произвольных «алфавитов», отличных от двоичных цифр 0 и 1, как описано ниже.

Передача более длинных сообщений

Чтобы анонимный отправитель мог передавать более одного бита информации за цикл DC-сети, группа криптографов может просто повторять протокол столько раз, сколько требуется, чтобы создать желаемое количество битов в полосе пропускания передачи. Эти повторы не нужно выполнять последовательно. В практических системах DC-net обычно пары участников заранее договариваются об одном общем «главном» секрете, используя Обмен ключами Диффи – Хеллмана Например. Затем каждый участник локально передает этот общий главный секрет в генератор псевдослучайных чисел, чтобы произвести столько общих «подбрасываний монеты», сколько требуется, чтобы анонимный отправитель мог передавать несколько битов информации.

Большие группы

Протокол можно обобщить на группу ${displaystyle n}$ участники, каждый из которых имеет общий секретный ключ, общий с другим участником. В каждом раунде протокола, если участник хочет передать группе не отслеживаемое сообщение, он инвертирует свой публично объявленный бит. Участников можно представить в виде полносвязный граф с вершинами, представляющими участников, и ребрами, представляющими их общие секретные ключи.

Редкие графики обмена секретами

Протокол может работать с неполностью подключенными графами совместного использования секрета, что может улучшить производительность и масштабируемость практических реализаций DC-сети с потенциальным риском снижения анонимности, если сговорившиеся участники могут разделить граф совместного использования секрета на отдельные подключенные компоненты. Например, интуитивно привлекательное, но менее безопасное обобщение на ${displaystyle n> 3}$ участники, использующие кольцевая топология, где каждый криптограф, сидящий за столом, делится секретом Только с криптографом слева и справа от них, и нет с каждым другим криптографом. Такая топология привлекательна, потому что каждому криптографу необходимо координировать два подбрасывания монеты за раунд, а не ${displaystyle n}$ . Однако, если Адам и Чарли на самом деле агенты АНБ, сидящие сразу слева и справа от Боба, невинной жертвы, и если Адам и Чарли тайно вступают в сговор, чтобы раскрыть друг другу свои секреты, то они могут с уверенностью определить, был ли Боб отправитель 1 бита в цепочке DC-net, независимо от того, сколько всего участников. Это связано с тем, что сговорившиеся участники Адам и Чарли эффективно «разбивают» граф совместного использования секрета на два отдельных несвязанных компонента, один из которых содержит только Боба, а другой - всех остальных честных участников.

Другой компромиссный вариант топологии DC-net с разделением секретов, используемый в Несогласие система масштабируемости,^[5] можно описать как клиент / сервер или же пользователь / попечитель топология. В этом варианте мы предполагаем, что есть два типа участников, играющих разные роли: потенциально большое количество п пользователей, которые хотят анонимности, и гораздо меньшее количество ${displaystyle m}$ из попечители чья роль состоит в том, чтобы помочь пользователям получить такую анонимность. В этой топологии каждый из ${displaystyle n}$ пользователи делятся секретом с каждым из ${displaystyle m}$ попечители - но пользователи не делятся секретами напрямую с другими пользователями, а опекуны не делятся секретами напрямую с другими опекунами, что приводит к ${displaystyle n imes m}$ матрица секретного обмена. Если количество попечителей ${displaystyle m}$ мала, то каждому пользователю нужно управлять только несколькими общими секретами, повышая эффективность пользователей так же, как и кольцевая топология. Однако пока хотя бы один попечитель ведет себя честно и не раскрывает свои секреты и не вступает в сговор с другими участниками, тогда этот честный опекун формирует «хаб», объединяющий всех честных пользователей в единый полностью связанный компонент, независимо от того, какие или сколько других пользователей и / или опекунов могут быть нечестный сговор. Пользователям не нужно знать или догадываться, какой доверительный управляющий честный; их безопасность зависит только от существование по крайней мере одного честного доверенного лица, не вступающего в сговор.

Альтернативные алфавиты и объединяющие операторы

Хотя простой протокол DC-nets использует двоичные цифры в качестве алфавита передачи и использует оператор XOR для объединения зашифрованных текстов, базовый протокол обобщается для любого алфавита и объединяет оператор, подходящий для одноразовый блокнот шифрование. Такая гибкость естественным образом проистекает из того факта, что секреты, общие для многих пар участников, по сути, представляют собой просто одноразовые планшеты, симметрично объединенные вместе в рамках одного раунда DC-сети.

Один полезный альтернативный выбор алфавита DC-сетей и оператора комбинирования - использовать конечная группа подходит для криптографии с открытым ключом в виде алфавита, например Группа Шнорра или же эллиптическая кривая - и использовать связанный групповой оператор в качестве оператора объединения DC-сети. Такой выбор алфавита и оператора позволяет клиентам использовать доказательство с нулевым разглашением методы для доказательства свойств правильности генерируемых ими шифровальных текстов DC-сети, например, что участник не «заглушает» канал передачи, без ущерба для анонимности, предлагаемой DC-net. Этот метод был впервые предложен Голлем и Джулсом,^[6] дальнейшее развитие Франк,^[7] и позже реализован в Вердикт, криптографически проверяемая реализация Несогласие система.^[8]

Обработка или предотвращение столкновений

Мера, первоначально предложенная Дэвидом Чаумом для предотвращения столкновений, заключается в повторной передаче сообщения после обнаружения столкновения, но в документе не объясняется, как именно организовать повторную передачу.

Несогласие позволяет избежать возможности непреднамеренных коллизий за счет использования проверяемого тасования для установления расписания передачи DC-сетей, так что каждый участник точно знает, какие биты в расписании соответствуют его собственному слоту передачи, но не знает, кто владеет другими слотами передачи.^[9]

Противодействие разрушающим атакам

Травоядное животное делит большую анонимную сеть на более мелкие группы DC-net, позволяя участникам уклоняться от попыток разрушения, покидая прерванную группу и присоединяясь к другой группе, пока участник не найдет группу, свободную от нарушителей.^[10] Такой подход уклонения создает риск того, что противник, владеющий множеством узлов, может выборочно разрушать только те группы, которых противник не полностью скомпрометированы, тем самым «загоняя» участников в группы, которые могут быть функциональными именно потому, что они полностью скомпрометированы.^[11]

Несогласие реализует несколько схем противодействия сбоям. Оригинальный протокол^[9] использовал поддающийся проверке криптографическое перемешивание формировать расписание передачи DC-сети и распределять «назначения передачи», позволяя проверять правильность последующих зашифрованных текстов DC-сети с помощью простого криптографический хеш проверить. Однако этот метод требовал новой проверки перед каждым раундом сети постоянного тока, что приводило к большим задержкам. Более поздняя, более эффективная схема позволяет продолжить серию раундов DC-net без прерывания перемешивания при отсутствии сбоев, но в ответ на событие сбоя использует перемешивание для распространения анонимных обвинения позволяя потерпевшему разоблачить и доказать личность преступника.^[5] Наконец, более поздние версии поддерживают полностью проверяемые сети постоянного тока - при значительных затратах на эффективность вычислений из-за использования криптография с открытым ключом в DC-net - а также гибридный режим, который использует эффективные DC-сети на основе XOR в нормальном случае и проверяемые DC-сети только при нарушении, чтобы распространять обвинения быстрее, чем это возможно при использовании проверяемых перетасовок.^[8]