Крышка края - Edge cover - Wikipedia

В теория графов, край крышки из график это набор края так что каждый вершина графа инцидентно хотя бы одному ребру множества. Информатика, то проблема минимального краевого покрытия Это проблема подбора кромочного покрытия минимального размера. Это проблема оптимизации что принадлежит к классу покрытие проблем и может быть решена в полиномиальное время.

Определение

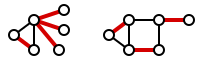
Формально краевое покрытие графа грамм это набор ребер C такая, что каждая вершина в грамм инцидентно хотя бы с одним ребром в C. Набор C говорят крышка вершины грамм. На следующем рисунке показаны примеры покрытий ребер в двух графах.

А минимальное краевое покрытие кромочное покрытие минимально возможного размера. В номер покрытия края ${ Displaystyle rho (G)}$ это размер минимального краевого покрытия. На следующем рисунке показаны примеры минимального покрытия кромок.

Обратите внимание, что рисунок справа - это не только крайняя крышка, но и соответствие. В частности, это идеальное соответствие: соответствие M в котором каждая вершина инцидентна ровно одному ребру из M. Идеальное совпадение (если оно существует) - это всегда минимальное краевое покрытие.

Примеры

Множество всех ребер является краевым покрытием при условии, что нет вершин нулевой степени.
В полный двудольный граф K_м,п имеет номер покрытия кромки max (м, п).

Алгоритмы

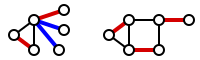
Самую маленькую краевую крышку можно найти в полиномиальное время найдя максимальное соответствие и жадно расширяем его так, чтобы все вершины были покрыты.^[1]^[2] На следующем рисунке максимальное совпадение отмечено красным; дополнительные ребра, которые были добавлены для покрытия несогласованных узлов, отмечены синим цветом. (На рисунке справа показан график, на котором максимальное совпадение идеальное соответствие; следовательно, он уже покрывает все вершины и никаких дополнительных ребер не требуется.)

С другой стороны, связанная с этим проблема поиска наименьшего крышка вершины является NP-жесткий проблема.^[1]

Смотрите также

Крышка Vertex
Установить обложку - проблема краевого покрытия - это частный случай задачи заданного покрытия: элементы вселенная вершины, и каждая подмножество охватывает ровно два элемента.

Примечания

^ ^а ^б Гэри и Джонсон (1979), п. 79, использует краевое покрытие и вершинное покрытие как один из примеров пары подобных задач, одна из которых может быть решена за полиномиальное время, а другая является NP-сложной. Также стр. 190.
^ Лоулер, Юджин Л. (2001), Комбинаторная оптимизация: сети и матроиды, Dover Publications, стр. 222–223, ISBN 978-0-486-41453-9.