Подающий барабан - Feed-Drum

В Подающий барабан[1] является имперский басовый барабан с системой электронного кондиционирования кожи, разработанной композитором Микеланджело Лупоне и совместно произведенной CRM - Centro Ricerche Musicali, Рим и Istituto Gramma в Аквиле.
По принципу Обратная связь, сигнал, производимый возбуждением кожи, возвращается к коже в виде акустическое давление. В результате получается бесконечно устойчивый звук. Система контролирует демпфирование движения кожи и, следовательно, скорость затухания звука, и позволяет изолировать высокочастотные моды за счет комбинированного воздействия узлов, присутствующих на коже, и количества входящей энергии обратной связи.[2]Рисунок на поверхности кожи представляет собой упрощенную карту колебательных режимов на основе Функции Бесселя. Карта была ограничена 13 диаметрами и 8 узловыми кругами, последние были разделены на четные полукруги (слева) и нечетные полукруги (справа).[3]Смотрите также Skin-Act.

Карта первых 13 узловых диаметров

Подающий барабан, первая карта с 13 диаметрами и 8 узловыми кругами
Экспериментальная работа
Хотя оболочка имперского большого барабана позволяет возбуждать значительное количество высокочастотных мод, их длительность во времени обычно незаметна для слушателя, за исключением тембрового вклада в фазу атаки звука. Возможные вариации режима излучения, адекватные для достаточного акустического отклика резонатора (оболочки), ограничены и имеют недостаточную модулируемость. Базовая частота, полученная путем натяжения обшивок, верхней и нижней, каждая из которых связана с краями с помощью 16 механических стяжек, зависит от неоднородного распределения сил натяжения, что способствует усложнению спектра реальных режимов. .[4]
Эксперименты проводились в Centro Ricerche Musicali - CRM в Риме.[5][6] и в Istituto Gramma в Аквиле с целью достижения этих целей:
- Изменение базовой частоты посредством наложения узловых ограничений на кожу
- Определение тембров по типу, режиму и точке возбуждения
- Звуковая модуляция с помощью глиссандо, вибрато, портаменто и ритмики. микроартикуляция
- Непрерывные или ступенчатые изменения динамики в зависимости от типа демпфирования, применяемого к коже.
Очевидно, что традиционные бас-барабаны не обладают этими характеристиками. Чтобы исследовать богатство тембра фазы атаки и изолировать колебательные моды, создатели создали систему для электронного управления кожей. Благодаря принципу обратной связи система возвращает сигнал, произведенный возбуждением кожи, обратно на кожу в виде акустического давления. Это дает бесконечное продолжение звука. Система управляет демпфированием кожи и, следовательно, скоростью затухания звука, и позволяет изолировать высокочастотные моды за счет комбинированного действия узлов, присутствующих на коже, и количества входящей энергии обратной связи.[7]
Стабильность сигнала, полученного с помощью этой системы кондиционирования, позволяет проводить эксперименты и создавать на поверхности кожи предварительную упрощенную карту колебательных режимов на основе функций Бесселя. Карта ограничена 13 диаметрами и 8 узловыми кругами, последние разделены на четные полукруги (слева) и нечетные полукруги (справа). Электронное кондиционирование инструмента оставляет неизменными топологию и основные акустические характеристики, но увеличивает объем вибрационных критериев и контроля. Это позволяло различать разные высоты тона различных мод, получать излучение длинных нот, которые можно было модулировать, как звуки, излучаемые натянутой струной, и адаптировать акустическую энергию независимо от излучаемых частот.[8]
Чтобы поддерживать маневренность и адекватную воспроизводимость явлений, первая классификация звуков и техник исполнения ограничивалась использованием пальцев, кистей и кистей рук (рис. 4). В составе Гран Касса Микеланджело Лупоне также проводил эксперименты с объектами разной формы и размеров, занимающими более широкие или множественные узловые секции. Это увеличило звуковые возможности. Однако сложность вибрационных явлений потребовала анализа механических частей прибора для выявления и уменьшения дисперсий и нелинейных вкладов от колебаний конструкционных материалов и их комбинаций.[9]

Рис.4 Подающий барабан, один из приемов возбуждения высокочастотных мод

Рис.5 Подающий барабан

Рис. 6 Обратная связь - 3 барабана подачи (2002 г.), отрывок из партитуры
Учитывая эти сложности, было решено спроектировать и реализовать новый инструмент, Feed-drum (рис. 5), с целью не только расширения акустических возможностей, но и обеспечения эргономичного использования новых исполнительных методов. В частности, отношение к вибрации было изменено за счет удаления нижней кожи, решение, которое упростило настройку базовой частоты инструмента (30 Гц) и уменьшило время нарастания возбуждения в верхних режимах. Была применена синтетическая мембрана с изотропными характеристиками и высокой гибкостью, на которой была нанесена ранее описанная карта с цветами, делающими области действия более заметными. Кожух и натяжная скоба были выполнены из стали и алюминия; в частности, натяжная скоба была сделана более жесткой при уменьшении высоты и увеличении поверхности сцепления. Система подвески была реализована таким образом, чтобы полностью отделить поток-барабан из опорной конструкции на земле; все механические части, контактирующие друг с другом, были разделены промежуточным слоем антивибрационного материала.[10]
Теория Операции
Поведение подающего барабана чрезвычайно сложно, и многие его аспекты еще предстоит выяснить. Ниже приведены известные, предположительные и еще не определенные элементы.
Режимы колебаний круглой нежесткой мембраны - прикрепленной вниз и растянутой вдоль ее края - известны из литературы. В консервативной модели (т. Е. Без диссипации и акустического излучения и, следовательно, «в вакууме») колебательные моды мембраны радиуса а имеют вид в цилиндрических координатах
(1)
куда: и
и где - функции Бесселя первого рода и порядка - произвольная фаза, зависящая от начальных условий (привилегированных направлений быть не может, поскольку проблема относится к круговой симметрии).
Из-за ограничения обода, , куда - радиус мембраны; это позволяет вычислить k (волновое число), которое является дискретным и зависит от двух индексов (m, n): , куда является корнем n-й степени из функции Бесселя порядка .
Следовательно (1) становится .
Следовательно, определение волнового числа возможно путем определения корней функции Бесселя первого рода. После определения корней и волновых чисел угловые частоты, характерные для мод, определяются как: где c - скорость распространения поперечных волн в мембране, куда сила растяжения обода и - поверхностная плотность мембраны. Тем не мение, можно легко оценить на основе частоты режима , самая низкая из всех (базовая частота), с учетом того, что :
Для подающего барабана, и , и поэтому .
Независимо от порядка функций Бесселя, корневая база стремится к за [2]; кроме того, функции Бесселя разного порядка не имеют совпадающих корней (важное соображение для целей Подающего барабана). Точный расчет корней может быть реализован только численно, что не представляет особой сложности с учетом колебательного характера (даже если не периодическое издание) функций Бесселя. Фактически, каждый корень этих функций находится между максимумом и минимумом или наоборот.
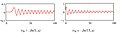
Рис.7 и Рис.8
Расчет частот для режимов до 5 октав выше «базовой частоты» (960 Гц для Подающего барабана) дает следующие распределения частот и модальной плотности:

Рис.9 и Рис.10

Рис.11
Индекс отвечает за создание узловых диаметров, индекс для узловых кругов. Как правило, характер режимов просто соотносится с индексами, как это видно из приведенных ниже диаграмм.
Система кондиционирования и реализация
Возбуждение мембраны осуществляется через громкоговоритель (Ø = 45 см) и волновод длиной 11 см (предназначенный для передачи максимального акустического давления между центром и 1/3 радиуса); то есть довольно короткие по форм-фактору. Оказалось, что довольно легко получить, помимо базовой частоты 30 Гц, частоту 68,9 Гц, соответствующую режиму (0,2). Напротив, получить частоту 47,8 Гц, соответствующую режиму (1,1), было невозможно. На этих частотах поведение воздуха, возбуждаемого громкоговорителем, предположительно можно схематически описать движением поршня, который оказывает почти равномерное давление на мембрану. Равномерное возбуждение плохо совместимо с модальной формой (1,1). Громкоговоритель приводился в действие сигналом электроэнергии, генерируемым системой обратной связи, которая дискретизирует сигнал, выдаваемый пьезокерамическим датчиком, размещенным на ободе и определяющим отклонение мембрана. Таким образом был получен «мультимодальный» осциллятор, генерирующий обратную связь на резонансном элементе - мембране. Контурное усиление регулировалось педалью.[11]
Интонация верхних ладов
Интонация происходит за счет комбинированного действия усиления отрицательной обратной связи и давления на одну или две точки узловой линии. Влияние давления можно схематически представить в первом приближении как двойное: с одной стороны, введение ограничения на точки давления, с другой стороны, смещение «рабочей точки» мембраны вокруг немного более высокого натяжения, и, следовательно, увеличение скорости поперечной волны . Следовательно, все частоты движутся вверх. Речь идет о механизме сдвига, «сдвиге высоты тона», в том смысле, что все частоты мод умножаются на общий коэффициент, поэтому их отношения остаются неизменными. Фактически, этот эффект встречается на практике и используется для получения вибрато. Однако термин «сдвиг высоты тона» в данном случае неуместен, поскольку спектр частичных тонов мембраны не является гармоническим, и в результате высота звука не определяется.
Сопоставление точек ограничения (z = 0), как правило, приводит к запрету каждого режима, в котором нет набора узловых линий, проходящих через все вышеупомянутые точки, даже при своевременном выборе .
Например, нажатие на центр мембраны делает все режимы с становится неосуществимым, поскольку эта точка неизменно является пучностью для этих мод. Давление на любую другую точку мембраны (говоря теоретически) заставляет все режимы с Это практически осуществимо, поскольку через эту точку всегда можно будет получить диаметр узла. На практике, поскольку ограничение не является идеальным, предпочтение будет отдаваться режиму, который имеет как узловой диаметр, так и узловую окружность, проходящую через эту точку. Следствием того, что функции Бесселя не совпадают корни, является то, что моды разного порядка m не могут иметь совпадающих узловых окружностей. Очевидно, что даже моды с одинаковым m и разными n не могут иметь совпадающих узловых окружностей. С другой стороны, две разные моды могут иметь совпадающие узловые диаметры, если отношение их индексов m является целым числом. Единственная точка давления, отличная от центра, идентифицирует моду, имеющую только диаметр и окружность, проходящую через эту точку. Однако точки, которые лучше «различают» частотные моды, находятся рядом с центром, потому что узловые круги становятся плотно упакованными по направлению к периметру, и поэтому одна точка имеет тенденцию располагать многие из них очень близко к себе. Следовательно, это первый узловой круг, самый внутренний, который лучше всего различает режимы, что также показывает дисперсионный анализ.
Теоретически давление на любые две точки мембраны может создать ограничения, несовместимые с любым режимом.
Однако все эти соображения лучше ограничить модами относительно низкого порядка. Фактически можно предположить, что приближение нежесткой мембраны приводит к менее достоверным результатам с увеличением порядка мод, поскольку основание узла имеет тенденцию становиться сравнимым с толщиной самой мембраны. Существуют также другие соображения. Классическое уравнение мембраны, обычно используемое для получения режимов, является полностью консервативным и не учитывает ни диссипацию из-за внутреннего трения, ни излучения. Оба последних являются механизмами, которые ослабляют частицы, вызывая их распад в отсутствие возбуждающей силы. Символическое решение уравнения, соответствующего описанному виброакустическому движению, определенно невозможно, даже если будут приняты сильно упрощающие гипотезы. Ее можно решить с помощью численных методов (таких как FEM, BEM и т. Д.), Но даже в этом случае - если учесть акусто-упругую связь и внутренние диссипации мембраны - проблема остается деликатной, и результаты должны быть проверено экспериментально. Однако даже в отсутствие решения можно отметить, что распад парциальных частиц связан с добротностью (Q) их резонанса и вызывает расширение спектральной линии - всегда тем заметнее, чем больше относительный режим затухает. Внутреннее трение пропорционально скорости изменения локальной кривизны, которая увеличивается с частотой. Следовательно, можно предположить, что, как и в случае натянутых струн, затухание мод увеличивается с увеличением их частоты. Следовательно, в верхних областях спектра, где моды близки друг к другу и сосредоточены (см. Рис. 9 и 10), передаточная функция мембраны более непрерывна, чем дискретна, с умеренными пиками на модальных частотах. В этих областях возбуждаемые моды менее точно определены и зависят от коэффициента усиления контура и частотных характеристик электронной схемы отрицательной обратной связи. И наоборот, переход от одной моды к другой соседней частоты мало влияет на результирующую частоту. Поэтому при построении будущей улучшенной карты для возбуждения мод необходимо предусмотреть разумный выбор пар точек, которые обеспечивают наиболее значительную дискриминацию между модами. Кроме того, модальные частоты должны быть проверены экспериментально, так как можно предположить, что частоты некоторых мод отклоняются от своих номинальных значений из-за наличия актуатора с относительным волноводом, ширина луча которого равна 1/3 диаметр мембраны. Измерение этих отклонений не может быть надежно определено с помощью теоретических соображений, поскольку общая модель слишком сложна и может быть решена (как уже было показано) только численными методами.
Дальнейшее развитие
Испытания, проведенные на сегодняшний день с композиторами и перкуссионистами, стимулировали предложения по расширению критериев контроля, использованию специальных ударников различных форм и размеров, а также применению самостоятельной техники рук.[12]Последующие разработки будут в основном касаться эргономических аспектов с составлением более точных узловых карт для более простого и немедленного использования. Кроме того, вполне возможны усовершенствования в электронной системе кондиционирования и в ее работе с целью улучшения управляемости излучения высоких обертонов.[13]
Смотрите также
Рекомендации
- ^ GRAME Rencontre Musicales Pluridisciplinaries 2006 г. Проверено 18 августа, 2009. В архиве 16 июля 2011 г. Wayback Machine
- ^ Мадридский университет Комплутенсе
- ^ Институт Макса Планка - Информатика
- ^ Exibart
- ^ Гран Касса и адаптивный барабан подачи инструментов - Компьютерное моделирование и поиск музыки - Сено, Лоренцо - Лупоне, Микеланджело - Springer Verlag 2006 - ISBN 3-540-34027-0
- ^ CRM - Centro Ricerche Musicali
- ^ Springer Berlin Heidelberg
- ^ ИНИСТ / CNRS
- ^ "LMA CNRS MRS France". Архивировано из оригинал на 2011-07-20. Получено 2009-08-21.
- ^ Консерватория музыки Альфредо Казелла L'Aquila В архиве 2016-03-03 в Wayback Machine Проверено 21 августа, 2009 г.
- ^ Corriere della Sera
- ^ ItaliaFestival
- ^ YouTube





































