GNU Archimedes - GNU Archimedes

Не путать с Архимед (CAD).

GNU Archimedes

Оригинальный автор (ы)	Жан Мишель Селье
Разработчики)	Проект GNU
Стабильный выпуск	2.0.1 / 30 апреля 2013 г.; 7 лет назад (2013-04-30)[1]
Операционная система	Linux, UNIX
Тип	TCAD
Лицензия	GPL
Интернет сайт	GNU.org/программного обеспечения/Архимед/

• Портал бесплатного программного обеспечения с открытым исходным кодом

Архимед это TCAD пакет для использования инженерами для разработки и моделирования субмикронных и мезоскопических полупроводниковых устройств. Архимед бесплатно программное обеспечение и поэтому его можно копировать, изменять и распространять под GPL. Архимед использует Ансамбль Монте-Карло метод и способен моделировать физические эффекты и перенос электронов и тяжелых дырок в кремнии, германии, GaAs, InSb, AlSb, AlAs, AlxInxSb, AlxIn (1-x) Sb, AlP, AlSb, GaP, GaSb, InP и их соединениях. (Полупроводниковые материалы III-V), а также оксид кремния. Приложенные и / или самосогласованные электростатические и магнитные поля обрабатываются с помощью Пуассон и уравнения Фарадея.

В Проект GNU объявила в мае 2012 года, что программный пакет Эней^[2] будет заменен Archimedes, что сделает его пакетом GNU для моделирования полупроводниковых устройств методом Монте-Карло.^[3]

Вступление

Archimedes - это пакет GNU для моделирования полупроводниковых устройств, который был впервые выпущен в 2005 году под GPL. Он был создан Жаном Мишелем Селье, который с тех пор является руководителем проекта и главным разработчиком. Это бесплатное программное обеспечение, поэтому его можно копировать, изменять и распространять по лицензии GPL. Это одно из больших преимуществ использования Archimedes.

Archimedes принадлежит к хорошо известному семейству программного обеспечения TCAD, то есть инструментов, используемых для помощи в разработке технологически значимых продуктов. В частности, этот пакет помогает инженерам в разработке и моделировании субмикронных и мезоскопический полупроводниковые приборы. В следующей версии Архимед также сможет моделировать наноустройства, используя формализм Вигнера Монте-Карло.^[4] (экспериментальный выпуск можно найти на^[5]). Сегодня Archimedes используется в нескольких крупных компаниях для моделирования и производства.

Архимед также полезен в учебных целях, поскольку каждый может получить доступ к источникам, изменить и протестировать их. Сегодня он используется для преподавания в нескольких сотнях университетов по всему миру. Кроме того, упрощенная версия, разработанная для студентов, доступна на nanoHUB.org.

В Ансамблевый метод Монте-Карло - это метод, который Архимед использует для моделирования и прогнозирования поведения устройств. Поскольку Monte Carlo очень стабилен и надежен, Archimedes можно использовать для определения характеристик устройства еще до того, как оно будет построено.

Физика и геометрия устройства описываются просто сценарием, что делает в этом смысле Archimedes мощным инструментом для моделирования довольно общих полупроводниковых устройств.

Архимед может моделировать множество физических эффектов и переноса электронов и тяжелых дырок в кремнии, германии, GaAs, InSb, AlSb, AlAs, AlxInxSb, AlxIn (1-x) Sb, AlP, AlSb, GaP, GaSb, InP и их соединения (полупроводниковые материалы III-V), наряду с оксидом кремния, применяют и / или самосогласованные электростатические и магнитные поля с помощью уравнения Пуассона и Фарадея. Он также может работать с гетероструктурами.

Уравнение переноса Больцмана

В Уравнение переноса Больцмана Модель была основным инструментом, используемым при анализе транспорта в полупроводниках. Уравнение BTE определяется следующим образом:

${\displaystyle {\frac {\partial f}{\partial t}}+{\frac {1}{\hbar }}\nabla _{k}E(k)\nabla _{r}f+{\frac {qF(r)}{\hbar }}\nabla _{k}f=\left[{\frac {\partial f}{\partial t}}\right]_{\mathrm {collision} }}$

${\displaystyle v={\frac {1}{\hbar }}\nabla _{k}E(k)}$

В функция распределения, ж, представляет собой безразмерную функцию, которая используется для извлечения всех представляющих интерес наблюдаемых и дает полное описание распределения электронов как в реальном, так и в k-пространство. Кроме того, он физически представляет собой вероятность заселения частицей энергии. k на позиции р и времят. Кроме того, из-за того, что это семимерное интегро-дифференциальное уравнение (шесть измерений в фазовом пространстве и одно во времени), решение BTE громоздко и может быть решено в замкнутой аналитической форме с очень специальными ограничениями. Численно решение для BTE используется либо детерминированным методом, либо стохастическим методом. Решение детерминированного метода основано на сеточном численном методе, таком как подход сферических гармоник, тогда как метод Монте-Карло - это стохастический подход, используемый для решения BTE.

Метод Монте-Карло

Полуклассический Метод Монте-Карло статистический метод, используемый для получения точного решения уравнения переноса Больцмана, которое включает комплексные ленточная структура и рассеяние процессы. Этот подход является полуклассическим по той причине, что механизмы рассеяния рассматриваются квантово-механически с использованием Золотое правило Ферми, тогда как перенос между событиями рассеяния рассматривается с использованием классического понятия частиц. Модель Монте-Карло, по сути, отслеживает траекторию частицы при каждом свободном полете и случайным образом выбирает соответствующий механизм рассеяния. Двумя большими преимуществами полуклассического Монте-Карло являются его способность обеспечивать точную квантово-механическую трактовку различных различных механизмов рассеяния в условиях рассеяния, а также отсутствие предположений о форме распределения носителей по энергии или k-пространству. Квазиклассическое уравнение, описывающее движение электрона, имеет вид

${\displaystyle {\frac {dr}{dt}}={\frac {1}{\hbar }}\nabla _{k}E(k)}$

${\displaystyle {\frac {dk}{dt}}={\frac {qF(r)}{\hbar }}}$

где F - электрическое поле, E (k) - соотношение дисперсии энергии, k - волновой вектор импульса. Чтобы решить указанное выше уравнение, необходимо хорошо знать зонную структуру (E (k)). Соотношение E (k) описывает, как частица движется внутри устройства, в дополнение к отображению полезной информации, необходимой для транспортировки, такой как плотность состояний (DOS) и скорость частицы. Полнодиапазонное соотношение E (K) может быть получено с помощью полуэмпирического метода псевдопотенциала.^[6]

Скриншоты

• 

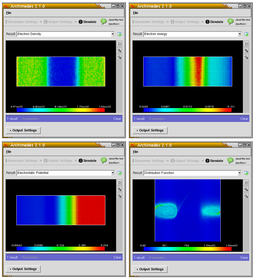
  Простое двухмерное моделирование диода с использованием Archimedes. Диод представляет собой простую структуру типа n + -n-n + с длиной канала 0,4 мкм. Диод имеет две n + области размером 0,3 микрона (то есть общая длина составляет 1,0 микрон). Плотность в областях легирования n + = 1.e23 / m ^ 3 и n = 1.e21 / m ^ 3 соответственно. Приложенное напряжение равно 2,0 Вольт.

• 

  Моделирование двумерного кремниевого MESFET с использованием Archimedes. Архимед учитывает все соответствующие механизмы рассеяния.

Рекомендации

1. Селье, Жан Мишель (30 апреля 2013 г.). «Выпущен Archimedes 2.0.1» (Список рассылки). info-gnu. Получено 2014-01-12.
2. «Эней», gnu.org, Май 2012 г.
3. Селье, Жан Мишель (13 мая 2012 г.). "Новый выпуск Энея" (Список рассылки). info-gnu. Получено 2012-05-13.
4. Э. Вигнер, О квантовой поправке на термодинамическое равновесие (1932).
5. Дж. М. Селье, http://www.nano-archimedes.com
6. К. Хесс, Моделирование устройств Монте-Карло: полный диапазон и не только, технологии (1991)

внешняя ссылка

• Официальный веб-сайт
• проект полного руководства
• руководство пользователя