Сканирование Грэма - Graham scan
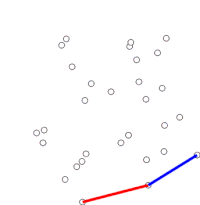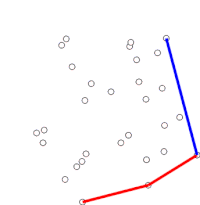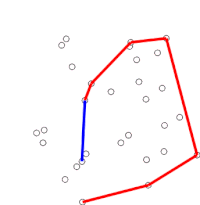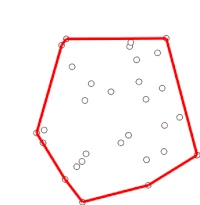
Скан Грэма это метод поиска выпуклая оболочка конечного множества точек на плоскости с временная сложность О (п журнал п). Он назван в честь Рональд Грэм, опубликовавший оригинальный алгоритм в 1972 году.[1] Алгоритм находит все вершины выпуклой оболочки, упорядоченные по ее границе. Он использует стек для эффективного обнаружения и удаления выемок на границе.
Алгоритм

Первый шаг в этом алгоритме - найти точку с наименьшей y-координатой. Если самая низкая координата Y существует более чем в одной точке в наборе, должна быть выбрана точка с самой низкой координатой x из возможных. Назовите эту точку п. Этот шаг требует О (п), где п количество рассматриваемых баллов.
Затем набор точек необходимо отсортировать в порядке возрастания угла между ними и точки. п сделать с осью абсцисс. Любой универсальный алгоритм сортировки подходит для этого, например heapsort (что составляет O (п журнал п)).
Сортировка по углу не требует вычисления угла. Можно использовать любую функцию угла, которая монотонна в интервал . Косинус легко вычисляется с помощью скалярное произведение, или может использоваться наклон линии. Если на карту поставлена числовая точность, функция сравнения, используемая алгоритмом сортировки, может использовать знак перекрестное произведение для определения относительных углов.
Алгоритм продолжается путем последовательного рассмотрения каждой точки в отсортированном массиве. Для каждой точки сначала определяется, составляет ли путешествие из двух точек, непосредственно предшествующих этой точке, поворот налево или поворот направо. При повороте направо предпоследняя точка не является частью выпуклой оболочки, а лежит «внутри» ее. Затем такое же определение выполняется для набора последней точки и двух точек, которые непосредственно предшествуют точке, находящейся внутри корпуса, и повторяется до тех пор, пока не встретится набор «левый поворот», после чего алгоритм переходит к к следующей точке в наборе точек в отсортированном массиве за вычетом любых точек, которые были обнаружены внутри корпуса; нет необходимости снова рассматривать эти моменты. (Если на каком-либо этапе три точки лежат на одной прямой, можно либо отбросить, либо сообщить об этом, поскольку в некоторых приложениях требуется найти все точки на границе выпуклой оболочки.)
Опять же, определение того, составляют ли три точки «левый поворот» или «правый поворот», не требует вычисления фактического угла между двумя отрезками прямой и фактически может быть достигнуто только с помощью простой арифметики. За три очка , и , вычислить z-координата перекрестное произведение из двух векторов и , который задается выражением . Если результат 0, точки коллинеарны; если он положительный, три точки образуют «левый поворот» или ориентацию против часовой стрелки, в противном случае - «правый поворот» или ориентацию по часовой стрелке (для точек, пронумерованных против часовой стрелки).
Этот процесс в конечном итоге вернется к точке, в которой он начался, на этом этапе алгоритм завершается, и теперь стек содержит точки на выпуклой оболочке в порядке против часовой стрелки.
Сложность времени
Сортировка точек имеет временную сложность O (п журнал п). Хотя может показаться, что временная сложность цикла составляет O (п2), потому что для каждой точки он возвращается, чтобы проверить, делает ли какая-либо из предыдущих точек «поворот вправо», на самом деле это O (п), потому что каждая точка в некотором смысле рассматривается не более двух раз. каждая точка может появляться только один раз как точка в «левом повороте» (потому что алгоритм переходит к следующей точке после этого), и как точка в "поворот направо" (потому что точка удален). Таким образом, общая временная сложность составляет O (п журнал п), поскольку время сортировки доминирует над временем фактического вычисления выпуклой оболочки.
Псевдокод
В приведенном ниже коде используется функция ccw: ccw> 0, если три точки совершают поворот против часовой стрелки, по часовой стрелке, если ccw <0, и коллинеарны, если ccw = 0. (В реальных приложениях, если координаты являются произвольными действительными числами, функция требует точное сравнение чисел с плавающей запятой, и нужно остерегаться числовых особенностей для "почти" коллинеарных точек.)
Затем пусть результат сохранится в стек.
позволять точки быть список точекпозволять стек = empty_stack ()найти самая низкая координата y и крайняя левая точка, называемая P0Сортировать точки полярным углом с P0, если несколько точек имеют одинаковый полярный угол, то сохраняются только самые дальниеза точка в points: # вытаскиваем последнюю точку из стека, если мы поворачиваем по часовой стрелке, чтобы достичь этой точки в то время как считать стек> 1 и против часовой стрелки(next_to_top (стек), top (stack), point) <= 0: поп стек От себя точка к стекконец
Теперь стопка содержит выпуклую оболочку, в которой точки ориентированы против часовой стрелки, а P0 - первая точка.
Вот, next_to_top () - это функция для возврата элемента на одну запись ниже вершины стека без изменения стека, и аналогично, верх() для возврата самого верхнего элемента.
Этот псевдокод адаптирован из Введение в алгоритмы.
Примечания
Та же основная идея работает также, если входные данные отсортированы по координате x, а не по углу, и корпус вычисляется в два этапа, создавая соответственно верхнюю и нижнюю части корпуса. Эта модификация была разработана А.М. Эндрю.[2] и известен как Алгоритм монотонной цепи Эндрю. Он имеет те же основные свойства, что и скан Грэма.[3]
Техника стека, используемая в сканировании Грэма, очень похожа на все ближайшие меньшие значения проблема, и параллельные алгоритмы для всех ближайших меньших значений также могут быть использованы (например, сканирование Грэма) для эффективного вычисления выпуклой оболочки отсортированных последовательностей точек.[4]
Числовая надежность
Числовая надежность - проблема, которую нужно решать в алгоритмах, использующих конечную точность плавающая точка компьютерная арифметика. В статье 2004 года анализировалась простая инкрементная стратегия, которую можно использовать, в частности, для реализации сканирования Грэма.[5] Заявленная цель статьи заключалась не в конкретном анализе алгоритма, а в предоставлении учебного примера того, что и как может дать сбой из-за вычислений с плавающей запятой в вычислительная геометрия.[5] Позже Д. Цзян и Н. Ф. Стюарт[6] подробно остановился на этом и с помощью обратный анализ ошибок сделал два основных вывода. Во-первых, выпуклая оболочка - это хорошо кондиционированный проблема, и поэтому можно ожидать алгоритмов, которые дадут ответ в пределах разумной погрешности. Во-вторых, они демонстрируют, что модификация сканирования Грэма, которую они называют Грэхэмом-Фортуном (включающая идеи Стивен Форчун для числовой стабильности[7]) действительно преодолевает проблемы конечной точности и неточных данных «насколько это возможно».
Смотрите также
использованная литература
- ^ Грэм, Р.Л. (1972). «Эффективный алгоритм определения выпуклой оболочки конечного плоского множества» (PDF). Письма об обработке информации. 1 (4): 132–133. Дои:10.1016/0020-0190(72)90045-2.
- ^ Эндрю, А. М. (1979). «Еще один эффективный алгоритм для выпуклой оболочки в двух измерениях». Письма об обработке информации. 9 (5): 216–219. Дои:10.1016/0020-0190(79)90072-3.
- ^ Де Берг, Марк; Чеонг, Отфрид; Ван Кревельд, Марк; Овермарс, Марк (2008). Алгоритмы и приложения вычислительной геометрии. Берлин: Springer. стр.2 –14. Дои:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.
- ^ Беркман, Омер; Шибер, Барух; Вишкин, Узи (1993). «Оптимальные двойные логарифмические параллельные алгоритмы, основанные на нахождении всех ближайших меньших значений». Журнал алгоритмов. 14 (3): 344–370. CiteSeerX 10.1.1.55.5669. Дои:10.1006 / jagm.1993.1018..
- ^ а б Кеттнер, Лутц; Мельхорн, Курт; Пион, Сильвен; Ширра, Стефан; Яп, Чи (2008). «Классные примеры задач устойчивости в геометрических вычислениях» (PDF). Вычислительная геометрия. 40 (1): 61–78. Дои:10.1016 / j.comgeo.2007.06.003. (Более ранняя версия была представлена в 2004 году на ESA'2004)
- ^ Д. Цзян и Н. Ф. Стюарт, Обратный анализ ошибок в вычислительной геометрии В архиве 2017-08-09 в Wayback Machine, Вычислительные науки и их приложения - ICCSA 2006, том 3980 серии Конспект лекций по информатике, стр 50-59
- ^ Fortune, S. Стабильное поддержание триангуляции точек в двух измерениях. Материалы 30-го ежегодного симпозиума IEEE по основам информатики Vol. 30, 494-499, 1989.
дальнейшее чтение
- Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001) [1990]. «33.3: Нахождение выпуклой оболочки». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. С. 949–955. ISBN 0-262-03293-7.

![[0, пи]](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e2a912eda6ef1afe46a81b518fe9da64a832751)







