Массив Хальбаха - Halbach array

Диаграмма потока массива Хальбаха

Массив Хальбаха, показывающий ориентацию магнитного поля каждой детали. Этот массив даст сильное поле внизу, в то время как поле выше погаснет.

Ориентация сильной и слабой стороны в линейном массиве Хальбаха (сильная сторона вверх)

Ориентация сильной и слабой стороны в линейном массиве Хальбаха (слабая сторона вверх)

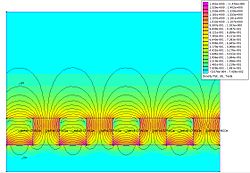
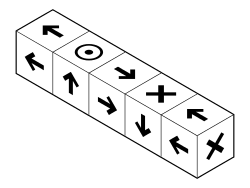
А Массив Хальбаха это особое расположение постоянных магниты который увеличивает магнитное поле на одной стороне массива, подавляя поле почти до нуля на другой стороне.^[1][2] Это достигается за счет наличия пространственно вращающегося шаблона намагничивания.

Вращающийся узор постоянных магнитов (на лицевой стороне; слева, вверх, справа, вниз) можно продолжать бесконечно долго и иметь тот же эффект. Эффект от такого расположения примерно аналогичен множеству подковообразных магнитов, размещенных рядом друг с другом, с соприкасающимися полюсами.

Эффект был обнаружен Джон К. Мэллинсон в 1973 году, и эти структуры «одностороннего потока» были первоначально описаны им как «любопытство», хотя в то время он осознал в этом открытии возможность значительного улучшения магнитная лента технологии.^[3]

Физик Клаус Хальбах, находясь в Национальная лаборатория Лоуренса Беркли в течение 1980-х независимо изобрел решетку Хальбаха для фокусировки лучей ускорителя частиц.^[4]

Линейные массивы Хальбаха

Намагничивание

Подавление магнитных компонентов, приводящее к одностороннему потоку

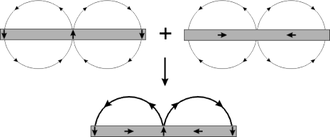
Хотя такое распределение магнитного потока кажется несколько нелогичным для тех, кто знаком с простыми стержневыми магнитами или соленоиды, причину такого распределения потока можно интуитивно визуализировать с помощью исходной диаграммы Маллинсона (обратите внимание, что здесь используется отрицательный у-компонент, в отличие от диаграммы в работе Мэллинсона). На схеме изображено поле из полосы ферромагнитный материал с переменной намагниченностью в у направлении (вверху слева) и в Икс направление (вверху справа). Обратите внимание, что поле над плоскостью находится в одно и тоже направление для обеих структур, но поле под плоскостью находится в противоположный направления. Эффект наложения обеих этих структур показан на рисунке:

Решающим моментом является то, что поток будет отменить под плоскостью и усилить себя над плоскостью. Фактически, любая картина намагничивания, в которой компоненты намагниченности ${\displaystyle \scriptstyle \pi /2}$ не совпадающие по фазе друг с другом, приведет к одностороннему потоку. Математическое преобразование, которое сдвигает фазу всех компонентов некоторой функции на ${\displaystyle \scriptstyle \pi /2}$ называется Преобразование Гильберта; поэтому компоненты вектора намагниченности могут быть любой парой преобразований Гильберта (простейшей из которых является просто ${\displaystyle \scriptstyle \sin(x)\cos(y)}$, как показано на диаграмме выше).

Магнитное поле вокруг бесконечного массива кубических магнитов Хальбаха. Поле не компенсируется идеально из-за используемых дискретных магнитов.

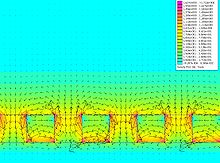
Поле на невозвратной стороне идеального, непрерывно изменяющегося бесконечного массива имеет вид:^[5]

${\displaystyle F(x,y)=F_{0}e^{ikx}e^{-ky}}$

куда:

${\displaystyle \scriptstyle F(x,y)}$ это поле в форме ${\displaystyle \scriptstyle F_{x}+iF_{y}}$

${\displaystyle \scriptstyle F_{0}}$ - величина поля на поверхности массива

${\displaystyle \scriptstyle k}$ пространственный волновое число, (т.е. пространственная частота) ${\displaystyle 2\pi /\lambda }$

Приложения

У одностороннего распределения потока два преимущества:

• Поле вдвое больше на той стороне, на которой ограничен поток (в идеализированном случае).
• Здесь нет блуждающее поле производится (в идеальном случае) с противоположной стороны. Это помогает с ограничением поля, что обычно является проблемой при проектировании магнитных структур.

Хотя односторонние распределения потока могут показаться несколько абстрактными, у них есть удивительное количество приложений, начиная от магнит на холодильник через промышленные применения, такие как бесщеточные Двигатель постоянного тока, звуковые катушки,^[6] магнитное нацеливание на наркотики ^[7] к высокотехнологичным приложениям, таким как виглер магниты, которые используются в ускорители частиц и лазеры на свободных электронах.

Это устройство также является ключевым компонентом Inductrack Поезд на магнитной подвеске^[8] и ракетная система запуска Inductrack.^[9] При этом массив Хальбаха отталкивает петли из проволоки, образующие рельсы после того, как поезд разгоняется до скорости, способной подниматься.

Распределение магнитного потока холодильника

Простейшим примером одностороннего магнитного потока является магнит на холодильник. Обычно они состоят из порошкового феррита в связке, такой как пластик или резина. В экструдированный Магнит подвергается действию вращающегося поля, придающего частицам феррита в магнитном соединении намагничивание, приводящее к одностороннему распределению потока. Такое распределение увеличивает удерживающую силу магнита, когда он помещен на проницаемую поверхность, по сравнению с удерживающей силой, скажем, от однородного намагничивания магнитного соединения.

Принципиальная схема лазера на свободных электронах

Увеличение размера этой конструкции и добавление верхнего листа дает магнит для вигглера, используемый в синхротроны и лазеры на свободных электронах. Магниты вигглера качают или колеблют электронный луч перпендикулярно магнитному полю. Когда электроны подвергаются ускорению, они излучают электромагнитную энергию в направлении своего полета, и, поскольку они взаимодействуют с уже испускаемым светом, фотоны вдоль его линии излучаются синфазно, в результате чего получается «подобный лазеру» монохроматический и когерентный луч.

Показанный выше дизайн обычно известен как вигглер Хальбаха. Векторы намагниченности в намагниченных листах вращаются в противоположных направлениях друг к другу; выше вектор намагниченности верхнего листа вращается по часовой стрелке, а вектор намагниченности нижнего листа вращается против часовой стрелки. Такой дизайн выбран так, чтобы Икс-компоненты магнитных полей из листов отменяют и у-компоненты усиливают так, что поле задано

${\displaystyle H_{y}\approx \cos(kx)}$

куда k это волновое число магнитного листа, заданного расстоянием между магнитными блоками с одинаковым вектором намагниченности.

Переменные линейные массивы

Схема массива Хальбаха, состоящего из ряда намагниченных стержней.

Равное зубчатое зацепление для переменного массива Хальбаха.

Ряд магнитных стержней, намагниченных перпендикулярно их осям, можно объединить в массив Хальбаха. Если затем каждый стержень поворачивать поочередно на 90 °, результирующее поле перемещается от одной стороны плоскости стержней к другой, как схематично показано на рисунке.

Такое расположение позволяет эффективно включать и выключать поле над или под плоскостью стержней, в зависимости от вращения стержней. Такое устройство создает эффективную механическую магнитную защелку, не требующую питания. Детальное изучение этого устройства показало, что каждый стержень подвергается сильному крутящему моменту со стороны соседних стержней и, следовательно, требует механической стабилизации.^[10] Однако простое и эффективное решение, обеспечивающее как стабилизацию, так и возможность попеременно вращать каждый стержень, состоит в том, чтобы просто обеспечить одинаковое зубчатое колесо на каждом стержне, как показано на рисунке.

Цилиндр Хальбаха

Ферромагнитный цилиндр, показывающий различные модели намагничивания и магнитное поле.

Намагничивание цилиндра.

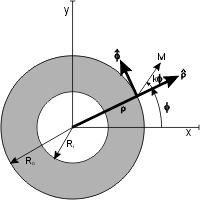
А Цилиндр Хальбаха представляет собой намагниченный цилиндр, состоящий из ферромагнитный материал, создающий (в идеализированном случае) сильное магнитное поле, полностью заключенное внутри цилиндра с нулевым полем снаружи. Цилиндры также могут быть намагничены так, чтобы магнитное поле находилось полностью вне цилиндра, а поле внутри было нулевым. Показаны несколько распределений намагниченности:

Направление намагничивания внутри ферромагнитного материала в плоскости, перпендикулярной оси цилиндра, определяется выражением

${\displaystyle M=M_{r}\left[\cos \left((k-1)\left(\varphi -{\frac {\pi }{2}}\right)\right){\widehat {\rho }}+\sin \left((k-1)\left(\varphi -{\frac {\pi }{2}}\right)\right){\widehat {\varphi }}\right]}$

куда M_р ферромагнетик остроту (Являюсь). Положительное значение k - 1 дает внутреннее магнитное поле, а отрицательное - внешнее магнитное поле.

В идеале эти структуры должны быть созданы из цилиндра бесконечной длины из магнитного материала с непрерывно изменяющимся направлением намагниченности. Магнитный поток, создаваемый этой идеальной конструкцией, был бы идеально однородным и полностью ограничивался бы отверстием цилиндра или внешней стороной цилиндра. Конечно, идеальный случай бесконечной длины не реализуем, и на практике конечная длина цилиндров дает конечные эффекты которые вносят в поле неоднородности.^[11][12] Сложность изготовления цилиндра с непрерывно изменяющейся намагниченностью также обычно приводит к разбивке конструкции на сегменты.

Приложения

Эти цилиндрические конструкции используются в таких устройствах, как бесщеточные двигатели переменного тока, магнитные муфты и цилиндры с сильным полем. И в бесщеточных двигателях, и в сцепных устройствах используется многополюсное устройство поля:

• В бесщеточных двигателях обычно используются цилиндрические конструкции, в которых весь поток ограничен центром отверстия (например, k = 4 выше, шестиполюсный ротор) с катушками переменного тока, также расположенными внутри отверстия. Такие конструкции двигателей с самозащитой более эффективны и создают более высокий крутящий момент, чем двигатели обычных конструкций.
• Устройства с магнитной муфтой передают крутящий момент через магнитно-прозрачные барьеры (то есть барьер немагнитный или магнитный, но на него не влияет приложенное магнитное поле), например, между герметичными контейнерами или сосудами под давлением. Оптимальная моментная муфта состоит из пары соосно размещенных цилиндров с противоположными +k и -k модели намагничивания магнитного потока, так как эта конфигурация является единственной системой для бесконечно длинных цилиндров, которые создают крутящий момент.^[13] В состоянии с наименьшей энергией внешний поток внутреннего цилиндра точно соответствует внутреннему потоку внешнего цилиндра. Вращение одного цилиндра относительно другого из этого состояния приводит к восстановлению крутящего момента.

Единые поля

Равномерное поле внутри цилиндра Гальбаха

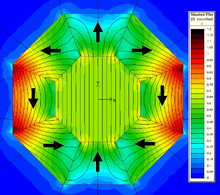
Для особого случая k = 2, поле внутри отверстия однородно и определяется выражением

${\displaystyle H=M_{r}\ln \left({\frac {R_{\text{o}}}{R_{\text{i}}}}\right){\widehat {y}},}$

где радиусы внутреннего и внешнего цилиндра равны р_я и р_о соответственно. ЧАС находится в у направление. Это простейшая форма цилиндра Хальбаха, и видно, что если отношение внешнего радиуса к внутреннему больше, чем е, поток внутри отверстия фактически превышает остроту магнитного материала, использованного для создания цилиндра. Однако следует проявлять осторожность, чтобы не создавать поля, которое превышает коэрцитивную силу используемых постоянных магнитов, так как это может привести к размагничиванию цилиндра и созданию поля гораздо меньшего, чем предполагалось.^[14][15]

Три конструкции (A) (B) (C), создающие однородные магнитные поля внутри их центрального воздушного зазора

Эта цилиндрическая конструкция - только один класс конструкций, которые создают однородное поле внутри полости внутри массива постоянных магнитов. К другим классам конструкций относятся конструкции с клином, предложенные Абеле и Дженсеном, в которых клинья из намагниченного материала расположены так, чтобы обеспечивать однородное поле внутри полостей внутри конструкции, как показано.

Направление намагничивания клиньев в (A) может быть вычислено с использованием набора правил, данных Абеле, и допускает большую свободу в форме полости. Другой класс конструкции - магнитный каток (B), предложенный Коуи и Кугатом,^[16][17] в котором равномерно намагниченные стержни расположены так, что их намагниченность соответствует намагниченности цилиндра Хальбаха, как показано для конструкции с 6 стержнями. Эта конструкция значительно увеличивает доступ к области однородного поля за счет меньшего объема однородного поля, чем в цилиндрических конструкциях (хотя эту область можно увеличить, увеличив количество стержней компонентов). Вращение стержней относительно друг друга дает множество возможностей, включая динамически изменяемое поле и различные дипольные конфигурации. Видно, что конструкции, показанные на (A) и (B), тесно связаны с k = 2 цилиндра Гальбаха. Другие очень простые конструкции для однородного поля включают отдельные магниты с обратными путями из мягкого железа, как показано на рисунке (C).

В последние годы эти диполи Хальбаха использовались для проведения слабопольных ЯМР эксперименты.^[18] По сравнению с коммерчески доступными (Bruker Minispec) стандартной геометрии пластин (C) постоянных магнитов, они, как объяснялось выше, имеют большой диаметр отверстия, но при этом имеют достаточно однородное поле.

Изменение поля

Цилиндры Хальбаха создают статическое поле. Однако цилиндры могут быть вложены друг в друга, и вращением одного цилиндра относительно другого можно добиться устранения поля и регулировки направления.^[19] Поскольку внешнее поле цилиндра довольно мало, относительное вращение не требует больших сил. В идеальном случае бесконечно длинных цилиндров для вращения одного цилиндра относительно другого не требуется силы.

Магнитная левитация с использованием планарной решетки Хальбаха и обмоток концентрической структуры

Сферы Хальбаха

Если двумерные картины магнитного распределения цилиндра Хальбаха расширить до трех измерений, в результате получится сфера Хальбаха. Эти конструкции имеют чрезвычайно однородное поле внутри конструкции, поскольку на них не влияют "конечные эффекты", преобладающие в конструкции цилиндров конечной длины. Величина однородного поля для сферы также увеличивается до 4/3 величины для идеальной цилиндрической конструкции с теми же внутренними и внешними радиусами. Однако, будучи сферической, доступ к области однородного поля обычно ограничен узким отверстием вверху и внизу конструкции.

Уравнение для поля в сфере Хальбаха имеет вид^[20]

${\displaystyle B={\frac {4}{3}}B_{0}\ln \left({\frac {R_{\text{o}}}{R_{\text{i}}}}\right).}$

Более высокие поля возможны путем оптимизации сферической конструкции с учетом того факта, что она состоит из точечных диполей (а не линейных диполей). Это приводит к растяжению сферы до эллиптической формы и к неравномерному распределению намагниченности по составным частям сферы. Используя этот метод, а также мягкие полюсные наконечники в конструкции, 4,5 Тл в рабочем объеме 20 мм.³ был достигнут Блохом и другие. в 1998 г.,^[21] и в 2002 году эта цифра была увеличена до 5 т.^[22] хотя при меньшем рабочем объеме 0,05 мм³. Поскольку твердые материалы зависят от температуры, охлаждение всего массива магнитов может еще больше увеличить поле в рабочей зоне, как показано Кумада. и другие. Эта группа также сообщила о разработке дипольного цилиндра Хальбаха 5,16 Т в 2003 году.^[23]

Катушка Гальбаха

Катушка матрицы Хальбаха

Массив Хальбаха может быть выполнен из катушек. Катушка массива Хальбаха по своей природе имеет более низкую индуктивность по сравнению с обычными катушками. Следовательно, матричная катушка Хальбаха может создавать относительно высокое магнитное поле при более низкой индуктивности и, следовательно, более высоком коэффициенте мощности по сравнению с обычными катушками.^[24]

Смотрите также

• Супермагнит
• Постоянный магнит
• Сильная фокусировка
• Inductrack использует массивы Хальбаха для генерации сильных полей для маглев
• Катушка Гельмгольца может давать очень ровные магнитные поля

Рекомендации

1. Клаус Хальбах (1980). «Конструкция постоянных многополюсных магнитов из ориентированного редкоземельного кобальта» (PDF). Ядерные инструменты и методы. 169 (1): 1–10. Bibcode:1980NucIM.169 .... 1H. Дои:10.1016 / 0029-554X (80) 90094-4. ISSN  0029-554X.
2. Клаус Хальбах (1985). «Применение постоянных магнитов в ускорителях и накопителях электронов» (PDF). Журнал прикладной физики. 57 (1): 3605–3608. Bibcode:1985JAP .... 57.3605H. Дои:10.1063/1.335021. ISSN  0029-554X.
3. Маллинсон Дж. К. (1973). «Односторонние потоки - магнитное любопытство?». IEEE Transactions on Magnetics. 9 (4): 678–682. Дои:10.1109 / TMAG.1973.1067714.
4. "Магнитно-левитирующий поезд взлетает | Новости науки Министерства энергетики США | EurekAlert! Новости науки". www.eurekalert.org.
5. «Архивная копия». Архивировано из оригинал 4 июня 2011 г.. Получено 31 августа 2008.
6. «Высокоэффективный мотор звуковой катушки».
7. А. Сарвар; А. Немировский; Б. Шапиро (2012). «Оптимальная конструкция постоянных магнитов Хальбаха для максимального вытягивания и выталкивания наночастиц» (PDF). Журнал магнетизма и магнитных материалов. 324 (5): 742–754. Bibcode:2012JMMM..324..742S. Дои:10.1016 / j.jmmm.2011.09.008. ЧВК  3547684. PMID  23335834.
8. Ричард Ф. Пост (10 октября 2005 г.). «На пути к более эффективному транспорту: система Inductrack Maglev» (PDF). Национальная лаборатория Лоуренса Ливермора. Получено 1 декабря 2017.
9. Л. С. Тунг; Р. Ф. Пост; Х. Мартинес-Фриас (27 июня 2001 г.). «Окончательный отчет о ходе разработки модели ракетной установки NASA Inductrack в Ливерморской национальной лаборатории имени Лоуренса» (PDF). UCRL-ID-144455. Архивировано из оригинал (PDF) 5 марта 2016 г.. Получено 12 января 2016.
10. Дж. Э. Хилтон; С. М. Макмерри (2012). «Регулируемая линейная решетка Хальбаха» (PDF). Журнал магнетизма и магнитных материалов. 324 (13): 2051–2056. Bibcode:2012JMMM..324.2051H. Дои:10.1016 / j.jmmm.2012.02.014. HDL:2262/63909.
11. Т. Р. Ни Миочейн; Д. Вир; С. М. Макмерри; Дж. М. Д. Коуи (1999). «Анализ крутящего момента в вложенных магнитных цилиндрах». Журнал прикладной физики. 86 (11): 6412–6424. Bibcode:1999JAP .... 86.6412N. Дои:10.1063/1.371705.
12. Р. Бьорк (2011). «Идеальные размеры цилиндра Хальбаха конечной длины». Журнал прикладной физики. 109 (1): 013915–013915–6. arXiv:1410.0496. Bibcode:2011JAP ... 109a3915B. Дои:10.1063/1.3525646. S2CID  119168717.
13. Р. Бьорк; А. Смит; К. Р. Х. Бахл (2010). «Анализ магнитного поля, силы и крутящего момента для двумерных цилиндров Хальбаха» (PDF). Журнал магнетизма и магнитных материалов. 322 (1): 133–141. arXiv:1409.1712. Bibcode:2010JMMM..322..133B. Дои:10.1016 / j.jmmm.2009.08.044. S2CID  56325133.
14. Р. Бьорк; А. Смит; К. Р. Х. Бахл (2015). «Эффективность и поле размагничивания обычного цилиндра Гальбаха» (PDF). Журнал магнетизма и магнитных материалов. 384: 128–132. arXiv:1502.06700. Bibcode:2015JMMM..384..128B. Дои:10.1016 / j.jmmm.2015.02.034. S2CID  54826296.
15. А. Р. Инсинга; К. Р. Х. Бахл; Р. Бьорк; А. Смит (2016). «Характеристики магнитных решеток Хальбаха с конечной коэрцитивной силой». Журнал магнетизма и магнитных материалов. 407: 369–376. Bibcode:2016JMMM..407..369I. Дои:10.1016 / j.jmmm.2016.01.076.
16. Дж. М. Д. Коуи; T.R. Ní Mhíocháin (2003). «Постоянные магниты». У Ф. Герлаха; Н. Миура (ред.). Сильные магнитные поля: наука и технологии. Том 1. Мировое научное издательство. С. 25–47. ISBN  978-981-02-4964-9.
17. О. Кугат; Ф. Блох; Ж. К. Туссен (1998). «Источник постоянного магнитного потока мощностью 4 Тесла». Proc. 15-й Международный семинар по редкоземельным магнитам и их применению: 807.
18. Райх, Х., Блюмлер, П., Проектирование и создание диполярной решетки Хальбаха с однородным полем из идентичных стержневых магнитов: ЯМР-мандалы в Концепции магнитного резонанса Часть B - Магнитно-резонансная инженерия 01/2004; 23B: 16–25.
19. "Журнал Tip: Магниты, рынки и магические цилиндры. Промышленный физик Майкла Коуи и Дениса Вира" (PDF). Архивировано из оригинал (PDF) 28 марта 2006 г.
20. Источники магнитного поля на основе постоянных магнитов.
21. Блох, Ф., Кугат, О., Менье, Г., Туссен, Дж. К. (1998). «Инновационные подходы к генерации сильных магнитных полей: разработка и оптимизация источника постоянного магнита 4 Тесла». IEEE Transactions on Magnetics. 34 (5): 2465–2468. Bibcode:1998ITM .... 34.2465B. Дои:10.1109/20.717567.
22. «Магнит-рекордсмен с полем в пять тесла - CERN Courier».
23. Кумада М., Антохин Е.И. и Ивашита, Ю., Аоки, М., Сугияма, Э. (2004). «Сверхсильный квадруполь с постоянным магнитом для линейного коллайдера» (PDF). IEEE Transactions по прикладной сверхпроводимости. 14 (2): 1287–1289. Bibcode:2004ITAS ... 14.1287K. Дои:10.1109 / TASC.2004.830555. S2CID  23698444.
24. «ИССЛЕДОВАНИЕ ОБМОТКИ ГАЛЬБАХОВСКОЙ МАССИНЫ».

внешняя ссылка

• Пассивная левитация вала
• Электромодель авиационного двигателя
• магнитная система переключения транспортных средств