Уравнение Ландау – Лифшица – Гильберта. - Landau–Lifshitz–Gilbert equation

В физике Уравнение Ландау – Лифшица – Гильберта., названный в честь Лев Ландау, Евгений Лифшиц, и Т. Л. Гилберт, это имя, используемое для дифференциальное уравнение описывая прецессионное движение из намагничивание M в твердый. Это модификация Гильбертом исходного уравнения Ландау и Лифшица.

Различные формы уравнения обычно используются в микромагнетизм смоделировать эффекты магнитное поле на ферромагнитные материалы. В частности, его можно использовать для моделирования поведения магнитных элементов во временной области под действием магнитного поля.^[1] В уравнение был добавлен дополнительный член для описания влияния спин-поляризованного тока на магниты.^[2]

Уравнение Ландау – Лифшица.

Члены уравнения Ландау – Лифшица – Гильберта: прецессия (красный цвет) и затухание (синий цвет). Траектория намагничивания (пунктирная спираль) построена в упрощающем предположении, что эффективное поле ЧАС_эфф постоянно.

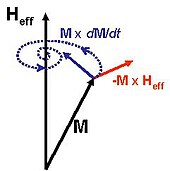
В ферромагнетик, то намагничивание M может меняться внутри, но в каждой точке его величина равна намагниченность насыщения M_s. Уравнение Ландау – Лифшица – Гильберта предсказывает вращение намагниченности в ответ на крутящие моменты. Более раннее, но эквивалентное уравнение (уравнение Ландау – Лифшица) было введено Ландау и Лифшиц (1935):^[3][4][5]

${displaystyle {frac {dmathbf {M} }{dt}}=-gamma mathbf {M} imes mathbf {H_{mathrm {eff} }} -lambda mathbf {M} imes left(mathbf {M} imes mathbf {H_{mathrm {eff} }} ight)}$

(1)

куда γ электрон гиромагнитное отношение. и λ - феноменологический параметр демпфирования, часто заменяемый на

${displaystyle lambda =alpha {frac {gamma }{M_{mathrm {s} }}},}$

куда α - безразмерная постоянная, называемая коэффициентом затухания. В эффективное поле ЧАС_эфф представляет собой комбинацию внешнего магнитного поля, размагничивающее поле (магнитное поле из-за намагниченности) и некоторые квантово-механические эффекты. Чтобы решить это уравнение, необходимо включить дополнительные уравнения для размагничивающего поля.

Используя методы необратимый статистическая механика, многочисленные авторы независимо получили уравнение Ландау – Лифшица.^[6]

Уравнение Ландау – Лифшица – Гильберта.

В 1955 году Гилберт заменил демпфирующий член в уравнении Ландау – Лифшица (ЛЛ) на член, который зависит от производной намагниченности по времени:

${displaystyle {frac {dmathbf {M} }{dt}}=-gamma left(mathbf {M} imes mathbf {H} _{mathrm {eff} }-eta mathbf {M} imes {frac {dmathbf {M} }{dt}}ight)}$

(2b)

Это уравнение Ландау – Лифшица – Гильберта (ЛЛГ), где η - параметр демпфирования, характерный для материала. Его можно преобразовать в уравнение Ландау – Лифшица:^[3]

${displaystyle {frac {dmathbf {M} }{dt}}=-gamma 'mathbf {M} imes mathbf {H} _{mathrm {eff} }-lambda mathbf {M} imes (mathbf {M} imes mathbf {H} _{mathrm {eff} })}$

(2а)

куда

${displaystyle gamma '={frac {gamma }{1+gamma ^{2}eta ^{2}M_{s}^{2}}}qquad { ext{and}}qquad lambda ={frac {gamma ^{2}eta }{1+gamma ^{2}eta ^{2}M_{s}^{2}}}.}$

В этой форме уравнения ЛЛ член прецессии γ ' зависит от срока демпфирования. Это лучше отражает поведение реальных ферромагнетиков при большом затухании.^[7]

Уравнение Ландау – Лифшица – Гильберта – Слончевского.

В 1996 г. Slonczewski расширил модель, чтобы учесть крутящий момент передачи вращения, т.е. крутящий момент, создаваемый при намагничивании вращение -поляризованный ток, протекающий через ферромагнетик. Обычно это выражается в единицах момента, определяемых как м = M / M_S:

${displaystyle {dot {mathbf {m} }}=-gamma mathbf {m} imes mathbf {H} _{mathrm {eff} }+alpha mathbf {m} imes {dot {mathbf {m} }}+ au _{parallel }{frac {mathbf {m} imes (mathbf {x} imes mathbf {m} )}{left|mathbf {x} imes mathbf {m} ight|}}+ au _{perp }{frac {mathbf {x} imes mathbf {m} }{left|mathbf {x} imes mathbf {m} ight|}}}$

куда ${displaystyle alpha }$ - безразмерный параметр затухания, ${displaystyle au _{perp }}$ и ${displaystyle au _{parallel }}$ крутящие моменты, и Икс - единичный вектор вдоль поляризации тока.^[8][9]

Ссылки и сноски

1. Ян, Бо. «Численные исследования динамического микромагнетизма». Получено 8 августа 2011.
2. «2.6.1 Уравнение Ландау-Лифшица-Гильберта с членом Слончевского, передающим спиновый момент».
3. Ахарони 1996
4. Браун-младший, 1978 г.
5. Тиказуми 1997
6. T. Iwata, J. Magn. Magn. Mater. 31–34, 1013 (1983); T. Iwata, J. Magn. Magn. Mater. 59, 215 (1986); В.Г. Баряхтар, Ж. Эксп. Теор. Физ. 87, 1501 (1984); С. Барта (не опубликовано, 1999 г.); W. M. Saslow, J. Appl. Phys. 105, 07D315 (2009).
7. Для получения подробной информации о нерезонансном эксперименте Келли и анализе Гилберта (который привел к изменению Гилбертом демпфирующего члена) см. T. L. Gilbert и J. M. Kelly, "Anomalous rotary damping in ferromагнитные листы", Conf. Магнетизм и магнитные материалы, Питтсбург, Пенсильвания, 14–16 июня 1955 г. (Нью-Йорк: Американский институт инженеров-электриков, октябрь 1955 г., стр. 253–263). http://people.physics.tamu.edu/saslow/MMMConf55_253GilbertKelly.pdf Текстовые ссылки на рисунки 5 и 6 должны были относиться к таблицам 1 и 2. Гилберт не мог соответствовать экспериментам Келли с фиксированным обычным гиромагнитным отношением. γ и частотно-зависимый λ=αγ, но может соответствовать этим данным для фиксированного гиромагнитного отношения Гилберта γ_грамм=γ/(1+α²) и частотно-зависимый α. Ценности α требовалось 9, что указывало на очень широкое поглощение и, следовательно, на образец относительно низкого качества. Современные образцы при анализе по резонансному поглощению дают αпорядка 0,05 или меньше.
8. Слончевский, Джон К. (1996). «Текущее возбуждение магнитных многослойных слоев». Журнал магнетизма и магнитных материалов. 159 (1): –1 – L7. Bibcode:1996JMMM..159L ... 1S. Дои:10.1016/0304-8853(96)00062-5.
9. Вольф, С. А. (16 ноября 2001 г.). «Спинтроника: взгляд на спин-ориентированную электронику будущего». Наука. 294 (5546): 1488–1495. Bibcode:2001Sci ... 294.1488W. Дои:10.1126 / science.1065389. PMID  11711666.

дальнейшее чтение

• Ахарони, Амикам (1996). Введение в теорию ферромагнетизма.. Clarendon Press. ISBN  978-0-19-851791-7.
• Браун-младший, Уильям Фуллер (1978) [Первоначально опубликовано в 1963 году]. Микромагнетизм. Роберт Э. Кригер Publishing Co. ISBN  978-0-88275-665-3.
• Тиказуми, Сошин (1997). Физика ферромагнетизма. Clarendon Press. ISBN  978-0-19-851776-4.
• Гилберт, Т. (1955). «Лагранжева формулировка гиромагнитного уравнения магнитного поля». Физический обзор. 100 (4): 1243. Bibcode:1955ПхРв..100.1235.. Дои:10.1103 / PhysRev.100.1235. Это всего лишь абстракция; полный отчет - «Проект Фонда исследований брони № A059, дополнительный отчет, 1 мая 1956 г.», но так и не был опубликован. Описание работы приведено в Гилберт, Т. Л. (2004). «Феноменологическая теория затухания в ферромагнетиках». IEEE Trans. Mag. 40 (6): 3443–3449. Bibcode:2004ITM .... 40.3443G. Дои:10.1109 / TMAG.2004.836740.
• Ландау, Л.; Лифшиц, Э. (1935). «Теория дисперсии магнитной проницаемости в ферромагнитных телах». Phys. Z. Sowjetunion. 8, 153.
• Скроцкий, Г. В. (1984). «Возвращение к уравнению Ландау – Лифшица». Сов. Phys. УСП. 27 (12): 977–979. Bibcode:1984СвФУ..27..977С. Дои:10.1070 / PU1984v027n12ABEH004101.
• Го, Болинг; Дин, Шицзинь (2008). Уравнения Ландау – Лифшица.. Границы исследований с Китайской академией наук. Всемирная научная издательская компания. ISBN  978-981-277-875-8.
• Цимрак, Иван (2007). "Обзор по численным и вычислительным методам для уравнения микромагнетизма Ландау – Лифшица" (PDF). Архивы вычислительных методов в технике. 15 (3): 1–37. Дои:10.1007 / BF03024947. Архивировано из оригинал (PDF) на 2015-07-05. Получено 2012-05-30.
• М, Лакшманан (2010). «Очаровательный мир уравнения Ландау – Лифшица – Гильберта: обзор». Фил. Пер. R. Soc. А. 369 (1939): 1280–1300. arXiv:1101.1005. Bibcode:2011RSPTA.369.1280L. Дои:10.1098 / rsta.2010.0319. PMID  21320917.

внешняя ссылка

• Апплет динамики намагничивания