Большой запас ближайшего соседа - Large margin nearest neighbor

Большой запас ближайшего соседа (LMNN)^[1] классификация статистический машинное обучение алгоритм за метрическое обучение. Он учится псевдометрический предназначен для k-ближайший сосед классификация. Алгоритм основан на полуопределенное программирование, подкласс выпуклая оптимизация.

Цель контролируемое обучение (более конкретно, классификация) заключается в изучении правила принятия решения, которое может классифицировать экземпляры данных в заранее определенные классы. В k-ближайший сосед правило предполагает обучение персонала набор данных помеченных экземпляров (т.е. классы известны). Он классифицирует новый экземпляр данных с классом, полученным в результате большинства голосов k ближайших (помеченных) обучающих экземпляров. Близость измеряется заранее определенным метрика. Большой запас ближайших соседей - это алгоритм, который изучает эту глобальную (псевдо) метрику контролируемым образом, чтобы повысить точность классификации правила k-ближайшего соседа.

Настраивать

Основная интуиция LMNN заключается в изучении псевдометрии, при которой все экземпляры данных в обучающем наборе окружены как минимум k экземплярами, которые имеют одну и ту же метку класса. Если это будет достигнуто, ошибка исключения одного значения (частный случай перекрестная проверка ) минимизируется. Пусть обучающие данные состоят из набора данных ${\displaystyle D=\{({\vec {x}}_{1},y_{1}),\dots ,({\vec {x}}_{n},y_{n})\}\subset R^{d}\times C}$, где набор возможных категорий классов ${\displaystyle C=\{1,\dots ,c\}}$.

Алгоритм изучает псевдометрию типа

${\displaystyle d({\vec {x}}_{i},{\vec {x}}_{j})=({\vec {x}}_{i}-{\vec {x}}_{j})^{\top }\mathbf {M} ({\vec {x}}_{i}-{\vec {x}}_{j})}$.

За ${\displaystyle d(\cdot ,\cdot )}$ чтобы быть корректным, матрица ${\displaystyle \mathbf {M} }$ должно быть положительный полуопределенный. Евклидова метрика - частный случай, когда ${\displaystyle \mathbf {M} }$ - единичная матрица. Это обобщение часто (ошибочно^{[нужна цитата ]}) именуемой Метрика Махаланобиса.

На рисунке 1 показано влияние метрики при изменении ${\displaystyle \mathbf {M} }$. Два кружка показывают набор точек с равным расстоянием до центра. ${\displaystyle {\vec {x}}_{i}}$. В евклидовом случае это множество представляет собой круг, тогда как в модифицированной метрике (Махаланобиса) оно становится кругом. эллипсоид.

Рисунок 1: Схематическое изображение LMNN.

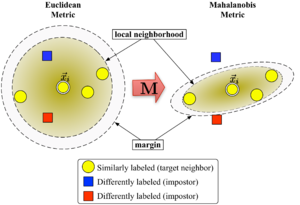
Алгоритм различает два типа специальных точек данных: целевые соседи и самозванцы.

Целевые соседи

Целевые соседи выбираются перед обучением. Каждый экземпляр ${\displaystyle {\vec {x}}_{i}}$ точно ${\displaystyle k}$ разные целевые соседи внутри ${\displaystyle D}$, которые имеют одну и ту же метку класса ${\displaystyle y_{i}}$. Целевые соседи - это точки данных, которые должен стать ближайшие соседи под выученной метрикой. Обозначим набор целевых соседей для точки данных ${\displaystyle {\vec {x}}_{i}}$ в качестве ${\displaystyle N_{i}}$.

Самозванцы

Самозванец точки данных ${\displaystyle {\vec {x}}_{i}}$ это еще одна точка данных ${\displaystyle {\vec {x}}_{j}}$ с другой меткой класса (т.е. ${\displaystyle y_{i}\neq y_{j}}$), который является одним из ближайших соседей ${\displaystyle {\vec {x}}_{i}}$. Во время обучения алгоритм пытается минимизировать количество самозванцев для всех экземпляров данных в обучающем наборе.

Алгоритм

Большой запас ближайших соседей оптимизирует матрицу ${\displaystyle \mathbf {M} }$ с помощью полуопределенное программирование. Задача двоякая: для каждой точки данных ${\displaystyle {\vec {x}}_{i}}$, то целевые соседи должно быть Закрыть и самозванцы должно быть далеко. Рисунок 1 показывает эффект такой оптимизации на иллюстративном примере. Полученная метрика вызывает входной вектор ${\displaystyle {\vec {x}}_{i}}$ быть окруженным обучающими экземплярами того же класса. Если бы это была контрольная точка, она была бы правильно отнесена к категории ${\displaystyle k=3}$ правило ближайшего соседа.

Первая цель оптимизации достигается за счет минимизации среднего расстояния между экземплярами и их целевыми соседями.

${\displaystyle \sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})}$.

Вторая цель достигается штрафными дистанциями до самозванцев. ${\displaystyle {\vec {x}}_{l}}$ которые менее чем на единицу дальше, чем целевые соседи ${\displaystyle {\vec {x}}_{j}}$ (и, следовательно, вытесняя их из окрестностей ${\displaystyle {\vec {x}}_{i}}$). Результирующее значение, которое необходимо минимизировать, может быть указано как:

${\displaystyle \sum _{i,j\in N_{i},l,y_{l}\neq y_{i}}[d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})]_{+}}$

С потеря петли функция ${\textstyle [\cdot ]_{+}=\max(\cdot ,0)}$, что гарантирует, что близость самозванца не наказывается за пределами поля. Запас ровно в одну единицу фиксирует масштаб матрицы ${\displaystyle M}$. Любой альтернативный выбор ${\displaystyle c>0}$ приведет к изменению масштаба ${\displaystyle M}$ в разы ${\displaystyle 1/c}$.

Конечная проблема оптимизации выглядит так:

${\displaystyle \min _{\mathbf {M} }\sum _{i,j\in N_{i}}d({\vec {x}}_{i},{\vec {x}}_{j})+\lambda \sum _{i,j,l}\xi _{ijl}}$

${\displaystyle \forall _{i,j\in N_{i},l,y_{l}\neq y_{i}}}$

${\displaystyle d({\vec {x}}_{i},{\vec {x}}_{j})+1-d({\vec {x}}_{i},{\vec {x}}_{l})\leq \xi _{ijl}}$

${\displaystyle \xi _{ijl}\geq 0}$

${\displaystyle \mathbf {M} \succeq 0}$

Гиперпараметр ${\textstyle \lambda >0}$ - некоторая положительная константа (обычно устанавливается посредством перекрестной проверки). Здесь переменные ${\displaystyle \xi _{ijl}}$ (вместе с двумя типами ограничений) заменяет член в функции стоимости. Они играют роль, подобную слабые переменные поглощать степень нарушений самозванца ограничений. Последнее ограничение гарантирует, что ${\displaystyle \mathbf {M} }$ положительно полуопределенный. Проблема оптимизации - это пример полуопределенное программирование (SDP). Хотя SDP, как правило, страдают высокой вычислительной сложностью, этот конкретный экземпляр SDP может быть решен очень эффективно из-за основных геометрических свойств проблемы. В частности, большинство ограничений самозванца удовлетворяются естественным образом, и их не нужно применять во время выполнения (т. Е. Набор переменных ${\displaystyle \xi _{ijl}}$разреженный). Особенно хорошо подходит метод решателя: рабочий набор , который сохраняет небольшой набор ограничений, которые активно применяются, и только время от времени отслеживает оставшиеся (вероятно выполненные) ограничения, чтобы гарантировать правильность.

Расширения и эффективные решатели

LMNN был расширен до нескольких локальных показателей в статье 2008 года.^[2] Это расширение значительно уменьшает ошибку классификации, но включает более дорогостоящую проблему оптимизации. В своей публикации 2009 года в Journal of Machine Learning Research,^[3] Вайнбергер и Саул выводят эффективный решатель для полуопределенной программы. Он может узнать метрику для Набор рукописных цифр MNIST за несколько часов, включая миллиарды попарных ограничений. An Открытый исходный код Matlab реализация находится в свободном доступе на веб-страница авторов.

Kumal et al.^[4] расширил алгоритм, включив локальные инварианты в многомерные полиномиальные преобразования и улучшенная регуляризация.

Смотрите также

• Изучение подобия
• Линейный дискриминантный анализ
• Изучение векторного квантования
• Псевдометрическое пространство
• Поиск ближайшего соседа
• Кластерный анализ
• Классификация данных
• Сбор данных
• Машинное обучение
• Распознавание образов
• Прогнозная аналитика
• Уменьшение размеров
• Анализ компонентов окружения

Рекомендации

1. Weinberger, K. Q .; Blitzer J. C .; Саул Л. К. (2006). «Дистанционное метрическое обучение для классификации ближайшего соседа с большой маржой». Достижения в системах обработки нейронной информации. 18: 1473–1480.
2. Weinberger, K. Q .; Саул Л. К. (2008). «Быстрые решатели и эффективные реализации для дистанционного метрического обучения» (PDF). Материалы международной конференции по машинному обучению: 1160–1167. Архивировано из оригинал (PDF) на 2011-07-24. Получено 2010-07-14.
3. Weinberger, K. Q .; Саул Л. К. (2009). «Дистанционное метрическое обучение для классификации с большой маржой» (PDF). Журнал исследований в области машинного обучения. 10: 207–244.
4. Kumar, M.P .; Torr P.H.S .; Зиссерман А. (2007). «Инвариантный классификатор ближайшего соседа с большим запасом». 11-я Международная конференция IEEE по компьютерному зрению (ICCV), 2007 г.: 1–8. Дои:10.1109 / ICCV.2007.4409041. ISBN  978-1-4244-1630-1.

внешняя ссылка

• Реализация Matlab
• ICML 2010 Учебное пособие по обучению метрикам