Самый низкий общий предок - Lowest common ancestor

Эта статья о низших общих предках в теории графов и информатике. Об общем предке набора видов в эволюционных деревьях см. самый последний общий предок. Об общем предке всех форм жизни см. последний универсальный общий предок.

В этом дереве самый низкий общий предок узлов Икс и у отмечен темно-зеленым. Остальные общие предки показаны светло-зеленым цветом.

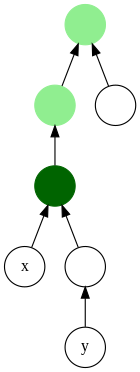
В теория графов и Информатика, то наименьший общий предок (LCA) двух узлов v и ш в дерево или же ориентированный ациклический граф (DAG) Т это самый низкий (то есть самый глубокий) узел, который имеет оба v и ш как потомки, где мы определяем каждый узел как потомок самого себя (так что если v имеет прямую связь с ш, ш является самым низким общим предком).

LCA v и ш в Т является общим предком v и ш который расположен дальше всего от корня. Вычисление наименьших общих предков может быть полезно, например, как часть процедуры определения расстояния между парами узлов в дереве: расстояние от v к ш может быть вычислено как расстояние от корня до v, плюс расстояние от корня до ш, минус удвоенное расстояние от корня до их наименьшего общего предка (Джиджев, Панциу и Заролягис 1991 ). В онтологии, самый низкий общий предок также известен как наименее общий предок.

В древовидная структура данных где каждый узел указывает на своего родителя, наименьшего общего предка можно легко определить, найдя первое пересечение путей из v и ш в корень. В общем, вычислительное время, необходимое для этого алгоритма, равно Ой) куда час - высота дерева (длина самого длинного пути от листа до корня). Однако существует несколько алгоритмов обработки деревьев, позволяющих быстрее находить самых низких общих предков. Автономный алгоритм наименьших общих предков Тарьяна, например, предварительно обрабатывает дерево за линейное время для предоставления запросов LCA с постоянным временем. В целом в DAG существуют похожие алгоритмы, но с суперлинейной сложностью.

История

Самая низкая проблема общего предка была определена Альфред Ахо, Джон Хопкрофт, и Джеффри Уллман  (1973 ), но Дов Харель и Роберт Тарджан  (1984 ) были первыми, кто разработал оптимально эффективную структуру данных с наименьшим общим предком. Их алгоритм обрабатывает любое дерево за линейное время, используя разложение тяжелого пути, так что последующие запросы с наименьшим общим предком могут быть даны ответы за постоянное время для каждого запроса. Однако их структура данных сложна и трудна для реализации. Тарьян также нашел более простой, но менее эффективный алгоритм, основанный на союз-находка структура данных, для вычисление наименьших общих предков автономного пакета пар узлов.

Барух Шибер и Узи Вишкин  (1988 ) упростил структуру данных Харела и Тарьяна, что привело к реализуемой структуре с той же асимптотической предварительной обработкой и временными рамками запроса. Их упрощение основано на том принципе, что в двух особых типах деревьев наименьших общих предков легко определить: если дерево является путем, то наименьший общий предок может быть вычислен просто из минимума уровней двух запрашиваемых узлов, а если дерево - полное двоичное дерево, узлы могут быть проиндексированы таким образом, чтобы самые низкие общие предки сводились к простым бинарным операциям над индексами. Структура Шибера и Вишкина разбивает любое дерево на набор путей, так что связи между путями имеют структуру двоичного дерева, и объединяет оба этих двух более простых метода индексации.

Омер Беркман и Узи Вишкин (1993 ) открыл совершенно новый способ ответа на запросы с наименьшим общим предком, снова достигнув линейного времени предварительной обработки при постоянном времени запроса. Их метод предполагает формирование Эйлер тур графа, сформированного из входного дерева путем удвоения каждого ребра, и использования этого тура для записи последовательности номеров уровней узлов в порядке их посещения туром; затем запрос наименьшего общего предка может быть преобразован в запрос, который ищет минимальное значение, встречающееся в некотором подынтервале этой последовательности чисел. Затем они справляются с этим минимальный запрос диапазона Проблема заключается в объединении двух методов, одна из которых основана на предварительном вычислении ответов на большие интервалы, размеры которых равны степеням двойки, а другая - на поиске в таблице для запросов с малым интервалом. Позднее этот метод был представлен в упрощенном виде Майклом Бендером и Мартин Фарач-Колтон  (2000 ). Как было ранее замечено Габоу, Бентли и Тарджан (1984), проблема минимума дальности, в свою очередь, может быть преобразована обратно в проблему с наименьшим общим предком, используя технику Декартовы деревья.

Дальнейшие упрощения были сделаны Alstrup et al. (2004) и Фишер и Хойн (2006).

Вариантом проблемы является проблема динамической LCA, в которой структура данных должна быть подготовлена ​​для обработки запросов LCA, смешанных с операциями, которые изменяют дерево (то есть переупорядочивают дерево путем добавления и удаления ребер). Этот вариант можно решить в ${\displaystyle O(\log N)}$ время^{[требуется дальнейшее объяснение ]} на все доработки и запросы. Это достигается за счет поддержки леса с использованием структуры данных динамических деревьев с секционированием по размеру; это затем поддерживает тяжелую-легкую декомпозицию каждого дерева и позволяет выполнять запросы LCA за логарифмическое время по размеру дерева.^{[нужна цитата ]}

Расширение на ориентированные ациклические графы

DAG с общими предками Икс и у светло-зеленым, а их самые низкие общие предки - темно-зеленым.

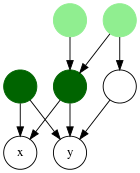
Первоначально изучаемое в контексте деревьев понятие наименьших общих предков может быть определено для ориентированных ациклических графов (DAG), используя любое из двух возможных определений. В обоих случаях предполагается, что края группы DAG указывают от родителей к детям.

• Данный грамм = (V, E), Aït-Kaci et al. (1989) определить посеть (V, ≤) такой, что Икс ≤ у если только Икс доступен из у. Самые низкие общие предки Икс и у тогда являются минимальными элементами под ≤ ≤ множества общих предков {z ∈ V | Икс ≤ z и у ≤ z}.
• Бендер и др. (2005) дали эквивалентное определение, где самые низкие общие предки Икс и у узлы высшая степень ноль в подграф из грамм индуцированный множеством общих предков Икс и у.

В дереве уникален самый низкий общий предок; в группе DAG п узлов, каждая пара узлов может иметь до п-2 LCA (Bender et al. 2005 г. ), в то время как существование LCA для пары узлов даже не гарантируется в произвольных подключенных DAG.

Алгоритм прямого перебора для поиска самых низких общих предков задается следующим образом: Aït-Kaci et al. (1989): найти всех предков Икс и у, затем верните максимальный элемент пересечения двух наборов. Существуют лучшие алгоритмы, которые, аналогично алгоритмам LCA для деревьев, предварительно обрабатывают граф, чтобы обеспечить выполнение запросов LCA с постоянным временем. Проблема Существование LCA можно оптимально решить для разреженных групп DAG с помощью O (|V||E|) алгоритм из-за Ковалук и Лингас (2005).

Dash et al. (2013) представляют собой единую структуру для предварительной обработки ориентированных ациклических графов для вычисления наименьших общих предков за постоянное время. Их структура может достигать почти линейного времени предварительной обработки для разреженных графов и доступна для публичного использования.^[1]

Приложения

Проблема вычисления низших общих предков классов в иерархия наследования возникает при реализации объектно-ориентированного программирования системы (Aït-Kaci et al. 1989 г. ). Проблема LCA также находит применение в моделях сложные системы нашел в распределенных вычислений (Bender et al. 2005 г. ).

Смотрите также

• Проблема предка уровня
• Полурешетка

Рекомендации

1. «Попробуйте наш исходный код бесплатно».

• Ахо, Альфред; Хопкрофт, Джон; Ульман, Джеффри (1973), «Об обнаружении самых низких общих предков на деревьях», Proc. 5-й симпозиум ACM. Теория вычислений (STOC), стр. 253–265, Дои:10.1145/800125.804056.
• Aït-Kaci, H .; Boyer, R .; Lincoln, P .; Наср, Р. (1989), «Эффективное выполнение решеточных операций» (PDF), Транзакции ACM по языкам и системам программирования, 11 (1): 115–146, CiteSeerX  10.1.1.106.4911, Дои:10.1145/59287.59293.
• Альструп, Стивен; Гавой, Сирил; Каплан, Хаим; Раухе, Тайс (2004), «Ближайшие общие предки: обзор и новый алгоритм для распределенной среды», Теория вычислительных систем, 37 (3): 441–456, CiteSeerX  10.1.1.76.5973, Дои:10.1007 / s00224-004-1155-5. Предварительная версия появилась в SPAA 2002.
• Бендер, Майкл А .; Фарач-Колтон, Мартин (2000), «Возвращение к проблеме LCA», Материалы 4-го латиноамериканского симпозиума по теоретической информатике, Конспект лекций по информатике, 1776, Springer-Verlag, стр.88–94, Дои:10.1007/10719839_9, ISBN  978-3-540-67306-4.
• Бендер, Майкл А .; Фарах-Колтон, Мартин; Пеммасани, Гиридхар; Скиена, Стивен; Сумазин, Павел (2005), «Наименьшие общие предки в деревьях и ориентированных ациклических графах» (PDF), Журнал алгоритмов, 57 (2): 75–94, Дои:10.1016 / j.jalgor.2005.08.001.
• Беркман, Омер; Вишкин, Узи (1993), «Рекурсивная структура параллельных данных типа« звезда-дерево »», SIAM Журнал по вычислениям, 22 (2): 221–242, Дои:10.1137/0222017.
• Даш, Сантану Кумар; Шольц, Свен-Бодо; Херхут, Стефан; Кристиансон, Брюс (2013), «Масштабируемый подход к вычислению репрезентативного наименьшего общего предка в ориентированных ациклических графах» (PDF), Теоретическая информатика, 513: 25–37, Дои:10.1016 / j.tcs.2013.09.030, HDL:2299/12152
• Джиджев, Христо Н .; Pantziou, Grammati E .; Зарольягис, Христос Д. (1991), "Вычисление кратчайших путей и расстояний в плоских графах", Автоматы, языки и программирование: 18-й международный коллоквиум, Мадрид, Испания, 8–12 июля 1991 г., Труды, Конспект лекций по информатике, 510, Springer, стр. 327–338, Дои:10.1007/3-540-54233-7_145, ISBN  978-3-540-54233-9.
• Фишер, Йоханнес; Хойн, Волкер (2006), «Теоретические и практические усовершенствования проблемы RMQ с приложениями к LCA и LCE», Материалы 17-го ежегодного симпозиума по комбинаторному сопоставлению с образцом, Конспект лекций по информатике, 4009, Springer-Verlag, стр. 36–48, CiteSeerX  10.1.1.64.5439, Дои:10.1007/11780441_5, ISBN  978-3-540-35455-0.
• Габоу, Гарольд Н .; Бентли, Джон Луи; Тарджан, Роберт Э. (1984), "Масштабирование и связанные с ним методы для геометрических задач", STOC '84: Proc. 16-й симпозиум ACM по теории вычислений, Нью-Йорк, Нью-Йорк, США: ACM, стр. 135–143, Дои:10.1145/800057.808675, ISBN  978-0897911337.
• Харел, Дов; Тарджан, Роберт Э. (1984), «Быстрые алгоритмы поиска ближайших общих предков», SIAM Журнал по вычислениям, 13 (2): 338–355, Дои:10.1137/0213024.
• Ковалук, Мирослав; Лингас, Анджей (2005), «LCA-запросы в ориентированных ациклических графах», в Кайресе, Луис; Итальяно, Джузеппе Ф.; Монтейро, Луис; Паламидесси, Катуша; Юнг, Моти (ред.), Автоматы, языки и программирование, 32-й международный коллоквиум, ICALP 2005, Лиссабон, Португалия, 11-15 июля 2005 г., Труды, Конспект лекций по информатике, 3580, Springer, стр.241–248, CiteSeerX  10.1.1.460.6923, Дои:10.1007/11523468_20, ISBN  978-3-540-27580-0
• Шибер, Барух; Вишкин, Узи (1988), «Об обнаружении низших общих предков: упрощение и распараллеливание», SIAM Журнал по вычислениям, 17 (6): 1253–1262, Дои:10.1137/0217079.

внешняя ссылка

• Самый низкий общий предок двоичного дерева поиска Камал Рават
• Реализация на Python алгоритма Бендера и Фараха-Колтона для деревьев, к Дэвид Эппштейн
• Реализация Python для произвольно направленных ациклических графов
• Конспект лекций по LCA из курса MIT Data Structures 2003. Курс по Эрик Демейн, заметки написаны Лоизосом Майклом и Христосом Капуцисом. Примечания от 2007 года, предлагающего тот же курс, написанный Элисон Циховлас.
• Самый низкий общий предок в двоичных деревьях в C. Упрощенная версия метода Шибера – Вишкина, работающая только для сбалансированных бинарных деревьев.
• видео из Дональд Кнут объяснение техники Шибера – Вишкина
• Минимальный запрос диапазона и статья о наименьшем общем предке в Topcoder
• Документация к пакету lca для Haskell Эдварда Кметта, который включает алгоритм асимметричного списка произвольного доступа. Чисто функциональные структуры данных для on-line LCA слайды для той же упаковки.