Проблема максимального подмассива - Maximum subarray problem

Визуализация изменения подмассивов в зависимости от начальной и конечной позиции образца. Каждый возможный непрерывный подмассив представлен точкой на цветной линии. Координата Y этой точки представляет собой сумму выборки. Его координата x представляет конец образца, а крайняя левая точка на этой цветной линии представляет начало образца. В этом случае массив, из которого берутся образцы, равен [2, 3, -1, -20, 5, 10].

В Информатика, то проблема подмассива максимальной суммы - задача найти непрерывный подмассив с наибольшей суммой в заданном одномерном массив [1 ... n] чисел. Формально задача найти индексы ${displaystyle i}$ и ${displaystyle j}$ с ${displaystyle 1leq ileq jleq n}$ , такая что сумма

{displaystyle sum _ {x = i} ^ {j} A [x]}

как можно больше. (Некоторые постановки задачи также позволяют рассматривать пустой подмассив; по соглашению сумма всех значений пустого подмассива равен нулю.) Каждое число во входном массиве A может быть положительным, отрицательным или нулевым.^[1]

Например, для массива значений [−2, 1, −3, 4, −1, 2, 1, −5, 4] непрерывный подмассив с наибольшей суммой равен [4, −1, 2, 1] , с суммой 6.

Некоторые свойства этой проблемы:

Если массив содержит все неотрицательные числа, проблема тривиальна; максимальный подмассив - это весь массив.
Если массив содержит все неположительные числа, то решением является любой подмассив размером 1, содержащий максимальное значение массива (или пустой подмассив, если это разрешено).
Несколько разных подмассивов могут иметь одинаковую максимальную сумму.

Эта проблема может быть решена с помощью нескольких различных алгоритмических методов, включая грубую силу,^[2] разделяй и властвуй,^[3] динамическое программирование,^[4] и сокращение до кратчайших путей.^{[нужна цитата ]}

История

Задача о максимуме подмассива была предложена Ульф Гренандер в 1977 г. как упрощенная модель для максимальная вероятность оценка закономерностей в оцифрованных изображениях.^[5]

Гренандер искал прямоугольный подмассив с максимальной суммой в двумерном массиве действительных чисел. Алгоритм грубой силы для двумерной задачи выполняется в О(п⁶) время; поскольку это происходило слишком медленно, Гренандер предложил одномерную задачу, чтобы понять ее структуру. Гренандер вывел алгоритм, решающий одномерную задачу в О(п²) время,^{[примечание 1]}улучшение времени работы грубой силы О(п³). Когда Майкл Шамос услышав о проблеме, он в одночасье придумал О(п бревно п) алгоритм разделяй и властвуй Вскоре после этого Шамос описал одномерную проблему и ее историю на Университет Карнеги Меллон семинар посетили Джей Кадейн, который за минуту разработал О(п) -временной алгоритм,^[5]^[6]^[7] что максимально быстро.^{[заметка 2]} В 1982 г. Дэвид Грис получил такой же О(п) -времени, применяя Dijkstra «стандартная стратегия»;^[8] в 1989 г., Ричард Берд получил его чисто алгебраическим манипулированием алгоритма грубой силы, используя Формализм Берда – Меертенса.^[9]

Двумерное обобщение Гренандера может быть решено за O (п³) времени либо с помощью алгоритма Кадане в качестве подпрограммы, либо с помощью подхода «разделяй и властвуй». Чуть более быстрые алгоритмы на основе умножение матрицы расстояний были предложены Тамаки и Токуяма (1998) и по Такаока (2002). Есть некоторые свидетельства того, что не существует значительно более быстрого алгоритма; алгоритм, который решает двумерную задачу о максимуме подмассива в O (п^{3 − ε}) времени для любого ε> 0 означало бы аналогичный быстрый алгоритм для кратчайшие пути для всех пар проблема.^[10]

Приложения

Проблемы с максимальным подмассивом возникают во многих областях, таких как геномная анализ последовательности и компьютерное зрение.

Анализ геномной последовательности использует алгоритмы максимального подмассива для идентификации важных биологических сегментов белковых последовательностей.^{[нужна цитата ]} Эти проблемы включают консервативные сегменты, GC-богатые области, тандемные повторы, фильтр низкой сложности, ДНК-связывающие домены и области с высоким зарядом.^{[нужна цитата ]}

В компьютерное зрение, алгоритмы максимального подмассива используются в растровых изображениях для обнаружения самой яркой области изображения.

Алгоритм Кадане

Пример запуска
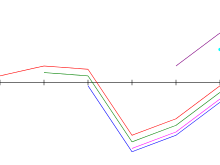
Выполнение алгоритма Кадане на над пример массива. Синий: подмассив с наибольшей суммой, заканчивающейся на я; зеленый: подмассив с наибольшей суммой, встреченной на данный момент; строчная буква указывает на пустой массив; переменная я остается неявным в коде Python.

Кадане алгоритм сканирует данный массив ${displaystyle A [1ldots n]}$ слева направо. в ${displaystyle j}$ -й шаг, он вычисляет подмассив с наибольшей суммой, заканчивающейся на ${displaystyle j}$ ; эта сумма сохраняется в переменной current_sum.^{[заметка 3]}Более того, он вычисляет подмассив с наибольшей суммой где-либо в ${displaystyle A [1ldots j]}$ , поддерживается в переменной best_sum,^{[примечание 4]}и легко получается как максимум из всех значений current_sum видно до сих пор, ср. строка 7 алгоритма.

Как инвариант цикла, в ${displaystyle j}$ -й шаг, старое значение current_sum держит максимум над всеми ${displaystyle iin {1, ldots, j}}$ суммы ${displaystyle A [i] + cdots + A [j-1]}$ .^{[примечание 5]}Следовательно, current_sum ${displaystyle + A [j]}$ ^{[примечание 6]}это максимум по всем ${displaystyle iin {1, ldots, j}}$ суммы ${displaystyle A [i] + cdots + A [j]}$ . Чтобы расширить последний максимум, чтобы охватить также случай ${displaystyle i = j + 1}$ , достаточно рассмотреть также пустой подмассив ${displaystyle A [j + 1; ldots; j]}$ . Это делается в строке 6 путем присвоения ${displaystyle max (0,})$ current_sum ${displaystyle + A [j])}$ как новое значение current_sum, который после этого имеет максимум по всем ${displaystyle iin {1, ldots, j + 1}}$ суммы ${displaystyle A [i] + cdots + A [j]}$ .

Таким образом, проблема может быть решена с помощью следующего кода,^[4]^[7] выражено здесь в Python:

1 def max_subarray(числа):2     "" "Найдите наибольшую сумму любого непрерывного подмассива." ""3     best_sum = 0  # или: float ('- inf')4     current_sum = 05     за Икс в числа:6         current_sum = Максимум(0, current_sum + Икс)7         best_sum = Максимум(best_sum, current_sum)8     вернуть best_sum

Эта версия алгоритма вернет 0, если входные данные не содержат положительных элементов (в том числе, когда вход пуст). Для варианта задачи, запрещающего пустые подмассивы, best_sum вместо этого следует инициализировать отрицательную бесконечность^[11] а также в цикле for current_sum следует обновить как макс (х, текущая_сумма + х).^{[примечание 7]}В этом случае, если входные данные не содержат положительного элемента, возвращаемое значение - это значение самого большого элемента (т. Е. Наименьшее отрицательное значение) или отрицательная бесконечность, если вход был пуст.

Алгоритм можно изменить, чтобы отслеживать начальные и конечные индексы максимального подмассива:

 1 def max_subarray(числа): 2     "" "Найдите непрерывный подмассив с наибольшей суммой." "" 3     best_sum = 0  # или: float ('- inf') 4     best_start = best_end = 0  # или: Нет 5     current_sum = 0 6     за current_end, Икс в перечислять(числа): 7         если current_sum <= 0: 8             # Начать новую последовательность с текущего элемента 9             current_start = current_end10             current_sum = Икс11         еще:12             # Расширить существующую последовательность текущим элементом13             current_sum += Икс14 15         если current_sum > best_sum:16             best_sum = current_sum17             best_start = current_start18             best_end = current_end + 1  # +1 делает 'best_end' эксклюзивным19 20     вернуть best_sum, best_start, best_end

В Python массивы индексируются, начиная с 0, а конечный индекс обычно исключается, так что подмассив [22, 33] в массиве [-11, 22, 33, -44] будет начинаться с индекса 1 и заканчиваться индексом 3.

Поскольку в этом алгоритме используются оптимальные подструктуры (максимальный подмассив, заканчивающийся в каждой позиции, вычисляется простым способом из связанной, но меньшей и перекрывающейся подзадачи: максимальный подмассив, заканчивающийся в предыдущей позиции), этот алгоритм можно рассматривать как простой / тривиальный пример динамическое программирование.

Сложность выполнения алгоритма Кадане составляет ${displaystyle O (n)}$ .^[4]^[7]

Обобщения

Подобные проблемы могут возникать и для многомерных массивов, но их решения более сложны; см., например, Такаока (2002). Бродал и Йоргенсен (2007) показал, как найти k наибольшие суммы подмассивов в одномерном массиве за оптимальное время ${displaystyle O (n + k)}$ .

Максимальная сумма k-связанные подмассивы также могут быть вычислены в оптимальной временной оценке ${displaystyle O (n + k)}$ .^[12]

Смотрите также

Проблема суммы подмножества

Примечания

^ Используя предварительно вычисленную таблицу накопленных сумм ${displaystyle S [k] = сумма _ {x = 1} ^ {k} A [x]}$ для вычисления суммы подмассива ${сумма стиля отображения _ {x = i} ^ {j} A [x] = S [j] -S [i-1]}$ в постоянное время
^ поскольку каждый алгоритм должен хотя бы один раз просканировать массив, который уже принимает О(п) время
^ названный MaxEndingHere в Бентли (1989), и c в Грис (1982)
^ названный МаксСофар в Бентли (1989), и s в Грис (1982)
^ Эта сумма ${displaystyle 0}$ когда ${displaystyle i = j}$ , соответствующий пустому подмассиву ${displaystyle A [jldots j-1]}$ .
^ В коде Python ${displaystyle A [j]}$ выражается как Икс, с индексом ${displaystyle j}$ слева неявно.
^ Хотя последняя модификация не упоминается Бентли (1989), он поддерживает инвариант измененного цикла current_sum ${displaystyle = max _ {iin {1, ..., j}} A [i] + ... + A [j]}$ в начале ${displaystyle j}$ -й шаг.

внешняя ссылка

ТАН, Лиронг. «Задачи о максимальной сумме непрерывных подмассивов» (PDF). Архивировано из оригинал (PDF) на 2015-10-10. Получено 2017-10-26.
Му, Шин-Ченг (2010). «Проблема максимальной суммы сегмента: ее происхождение и вывод».
«Примечания к проблеме максимального подмассива». 2012.
www.algorithmist.com
alexeigor.wikidot.com
проблема наибольшей подпоследовательной суммы на Розеттском коде
Страница geeksforgeeks по алгоритму Кадане

[6] Используя предварительно вычисленную таблицу накопленных сумм ${displaystyle S [k] = сумма _ {x = 1} ^ {k} A [x]}$ для вычисления суммы подмассива ${сумма стиля отображения _ {x = i} ^ {j} A [x] = S [j] -S [i-1]}$ в постоянное время

[9] поскольку каждый алгоритм должен хотя бы один раз просканировать массив, который уже принимает О(п) время

[13] названный MaxEndingHere в Бентли (1989), и c в Грис (1982)

[14] названный МаксСофар в Бентли (1989), и s в Грис (1982)

[15] Эта сумма ${displaystyle 0}$ когда ${displaystyle i = j}$ , соответствующий пустому подмассиву ${displaystyle A [jldots j-1]}$ .

[16] В коде Python ${displaystyle A [j]}$ выражается как Икс, с индексом ${displaystyle j}$ слева неявно.

[18] Хотя последняя модификация не упоминается Бентли (1989), он поддерживает инвариант измененного цикла current_sum ${displaystyle = max _ {iin {1, ..., j}} A [i] + ... + A [j]}$ в начале ${displaystyle j}$ -й шаг.

[FOOTNOTEBentley198969-1] Бентли 1989, п. 69.

[FOOTNOTEBentley198970-2] Бентли 1989, п. 70.

[FOOTNOTEBentley198973-3] Бентли 1989, п. 73.

[FOOTNOTEBentley198974-4] а ^б ^c Бентли 1989, п. 74.

[FOOTNOTEBentley1984868-869-5] а ^б Бентли 1984 года, п. 868-869.

[FOOTNOTEBentley198976-77-7] Бентли 1989, п. 76-77.

[FOOTNOTEGries1982211-8] а ^б ^c Грис 1982, п. 211.

[FOOTNOTEGries1982209-211-10] Грис 1982, п. 209-211.

[FOOTNOTEBird1989Sect.8,_p.126-11] Птица 1989, Раздел 8, стр.126.

[FOOTNOTEBackursDikkalaTzamos2016-12] Бэкурс, Диккала и Цамос 2016.

[FOOTNOTEBentley198978,171-17] Бентли 1989, п. 78 171.

[FOOTNOTEBengtssonChen2007-19] Бенгтссон и Чен 2007.

[1]

[2]

[3]

[4]

[5]

[примечание 1]

[6]

[7]

[заметка 2]

[8]

[9]

[10]

[заметка 3]

[примечание 4]

[примечание 5]

[примечание 6]

[11]

[примечание 7]

[12]