Мета-оптимизация - Meta-optimization

В численная оптимизация, метаоптимизация - это использование одного метода оптимизации для настройки другого метода оптимизации. Сообщается, что метаоптимизация использовалась еще в конце 1970-х годов Мерсером и Сэмпсоном.[1] для поиска оптимальных настроек параметров генетический алгоритм.
Метаоптимизация и связанные с ней концепции также известны в литературе как метаэволюция, супероптимизация, автоматическая калибровка параметров, гиперэвристика, так далее.
Мотивация

Методы оптимизации, такие как генетический алгоритм и дифференциальная эволюция имеют несколько параметров, которые определяют их поведение и эффективность при оптимизации данной задачи, и эти параметры должны быть выбраны практикующим специалистом для достижения удовлетворительных результатов. Выбор поведенческих параметров вручную - это трудоемкая задача, которая подвержена ошибочным представлениям людей о том, что обеспечивает хорошую работу оптимизатора.
Поведенческие параметры оптимизатора можно варьировать, а эффективность оптимизации отображать в виде ландшафта. Это выполнимо с вычислительной точки зрения для оптимизаторов с небольшим количеством поведенческих параметров и проблемами оптимизации, которые быстро вычисляются, но когда количество поведенческих параметров увеличивается, время, затрачиваемое на вычисление такого ландшафта производительности, увеличивается экспоненциально. Это проклятие размерности для поискового пространства, состоящего из поведенческих параметров оптимизатора. Следовательно, необходим эффективный метод поиска в пространстве поведенческих параметров.
Методы
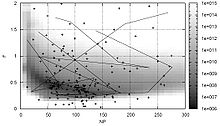
Простой способ найти хорошие поведенческие параметры для оптимизатора - использовать другой оптимизатор наложения, называемый мета -оптимизатор. Есть разные способы сделать это в зависимости от того, настроены ли поведенческие параметры, которые нужно настроить. ценный или дискретнозначный, и в зависимости от того, какой показатель производительности используется, и т. д.
Метаоптимизация параметров генетический алгоритм сделал Грефенстетте [2] и Кин,[3] среди прочего, и эксперименты с метаоптимизацией как параметров, так и генетические операторы сообщил Бэк.[4] Метаоптимизация алгоритма COMPLEX-RF была проведена Крусом и Андерссоном,[5] и,[6] где был введен и развит индекс эффективности оптимизации на основе теории информации. Мета-оптимизация оптимизация роя частиц было сделано Meissner et al.,[7] Педерсен и Чипперфилд,[8] и Mason et al.[9] Педерсен и Чипперфилд применили метаоптимизацию к дифференциальная эволюция.[10] Birattari et al.[11][12] мета-оптимизированный оптимизация колонии муравьев. Статистические модели также использовались, чтобы узнать больше о взаимосвязи между выбором поведенческих параметров и производительностью оптимизации, см., например, Франсуа и Лавернь,[13] и Наннен и Эйбен.[14] Сравнение различных методов метаоптимизации было проведено Смитом и Эйбеном.[15]
Смотрите также
использованная литература
- ^ Mercer, R.E .; Сэмпсон, Дж. Р. (1978). «Адаптивный поиск с использованием репродуктивного метаплана». Kybernetes. 7 (3): 215–228. Дои:10.1108 / eb005486.
- ^ Грефенстетте, Дж. Дж. (1986). «Оптимизация параметров управления генетическими алгоритмами». IEEE Transactions по системам, человеку и кибернетике. 16 (1): 122–128. Дои:10.1109 / TSMC.1986.289288.
- ^ Кин, А.Дж. (1995). «Оптимизация генетических алгоритмов в многопиковых задачах: исследования сходимости и устойчивости». Искусственный интеллект в инженерии. 9 (2): 75–83. Дои:10.1016 / 0954-1810 (95) 95751-Q.
- ^ Бэк, Т. (1994). «Параллельная оптимизация эволюционных алгоритмов». Труды Международной конференции по эволюционным вычислениям. С. 418–427.
- ^ Krus, PK .; Андерссон (Олвандер), Дж. (2003). «Оптимизация оптимизации для оптимизации дизайна». Материалы конференции DETC’03 2003 ASME Design Engineering Technical и Computers and Information in Engineering Conference Чикаго, Иллинойс, США.
- ^ Krus, PK .; Олвандер (Андерссон), Дж. (2013). «Индекс эффективности и метаоптимизация метода прямой поисковой оптимизации» (PDF). Инженерная оптимизация. 45 (10): 1167–1185. Bibcode:2013EnOp ... 45,1167K. Дои:10.1080 / 0305215X.2012.725052.
- ^ Meissner, M .; Schmuker, M .; Шнайдер, Г. (2006). «Оптимизация роя частиц (OPSO) и ее применение для обучения искусственной нейронной сети». BMC Bioinformatics. 7 (1): 125. Дои:10.1186/1471-2105-7-125. ЧВК 1464136. PMID 16529661.
- ^ Pedersen, M.E.H .; Чипперфилд, А.Дж. (2010). «Упрощение оптимизации роя частиц». Прикладные мягкие вычисления. 10 (2): 618–628. CiteSeerX 10.1.1.149.8300. Дои:10.1016 / j.asoc.2009.08.029.
- ^ Мейсон, Карл; Дагган, Джим; Хоули, Энда (2018). «Мета-оптимизационный анализ уравнений обновления скорости оптимизации роя частиц для обучения управлению водосбором». Прикладные мягкие вычисления. 62: 148–161. Дои:10.1016 / j.asoc.2017.10.018.
- ^ Педерсен, M.E.H. (2010). Настройка и упрощение эвристической оптимизации (PDF) (Кандидатская диссертация). Университет Саутгемптона, Школа инженерных наук, Группа вычислительной инженерии и дизайна.
- ^ Бираттари, М .; Stützle, T .; Paquete, L .; Варрентрапп, К. (2002). «Гоночный алгоритм для настройки метаэвристики». Труды конференции по генетическим и эволюционным вычислениям (GECCO). С. 11–18.
- ^ Бираттари, М. (2004). Проблема настройки метаэвристики с точки зрения машинного обучения (PDF) (Кандидатская диссертация). Université Libre de Bruxelles.
- ^ Francois, O .; Лавернь, К. (2001). «Дизайн эволюционных алгоритмов - статистическая перспектива». IEEE Transactions по эволюционным вычислениям. 5 (2): 129–148. Дои:10.1109/4235.918434.
- ^ Nannen, V .; Эйбен, А.Е. (2006). «Метод калибровки параметров и оценки релевантности в эволюционных алгоритмах» (PDF). Труды 8-й ежегодной конференции по генетическим и эволюционным вычислениям (GECCO). С. 183–190.
- ^ Смит, С.К .; Эйбен, А.Е. (2009). «Сравнение методов настройки параметров для эволюционных алгоритмов» (PDF). Труды Конгресса IEEE по эволюционным вычислениям (CEC). С. 399–406.
