Остовное дерево с минимальным узким местом - Minimum bottleneck spanning tree

В математике минимальное остовное дерево узких мест (MBST) в неориентированном графе есть остовное дерево в котором самое дорогое лезвие максимально дешево. Ребро узкого места - это край с самым высоким весом в остовном дереве. Остовное дерево является остовным деревом с минимальным узким местом, если граф не содержит остовного дерева с меньшим весом ребра узкого места.^[1] Для ориентированного графа аналогичная проблема известна как Арборесценция с минимальным узким местом (MBSA).

Определения

Ненаправленные графы

Остовное дерево с минимальным узким местом ${\displaystyle G(V,E)}$

В неориентированном графе грамм(V, E) и функция ш : E → р, позволять S быть набором всех остовных деревьев Т_я. Позволять B(Т_я) - ребро с максимальным весом для любого остовного дерева Т_я. Мы определяем подмножество остовных деревьев с минимальным узким местом S′ Такой, что для каждого Т_j ∈ S′ и Т_k ∈ S у нас есть B(Т_j) ≤ B(Т_k) для всех я иk.^[2]

График справа является примером MBST, красные ребра в графе образуют MBST грамм(V, E).

Направленные графы

Минимальное узкое место, охватывающее древообразование G (V, E)

Древообразование графа грамм направленное дерево грамм который содержит направленный путь от указанного узла L каждому узлу подмножества V' из V \{L}. Узел L называется корнем древесного происхождения. Древообразование - это протяженное древообразование, если V′ = V \{L}. MBST в данном случае представляет собой протяженное древообразование с минимальной границей узкого места. MBST в этом случае называется арборесценцией минимального узкого места (MBSA).

График справа является примером MBSA, красные ребра в графе образуют MBSA. грамм(V, E).

Характеристики

MST (или минимальное остовное дерево ) обязательно является MBST, но MBST не обязательно является MST.^[3]

^[4]

Алгоритм Камерини для неориентированных графов

Камерини предложил^[5] ан алгоритм используется для получения минимального остовного дерева узких мест (MBST) в данном неориентированном, подключенном, реберно-взвешенный граф в 1978 году. Он наполовину делит ребра на два набора. Вес ребер в одном наборе не больше, чем в другом. Если остовное дерево существует в подграфе, составленном только из ребер в наборе меньших ребер, затем он вычисляет MBST в подграфе, MBST подграфа в точности совпадает с MBST исходного графа. Если остовное дерево не существует, он объединяет каждый отсоединенный компонент в новую супервершину, затем вычисляет MBST в графе, образованном этими супервершинами и ребрами в большом наборе ребер. Лес в каждом отключенном компоненте является частью MBST в исходном графе. Повторяйте этот процесс до тех пор, пока в графе не останутся две (супер) вершины и не будет добавлено одно ребро с наименьшим весом между ними. Обнаруживается MBST, состоящий из всех ребер, найденных на предыдущих шагах.^[4]

Псевдокод

У процедуры есть два входных параметра. грамм это график, ш представляет собой массив весов всех ребер в графе грамм.^[6]

 1  функция MBST (график грамм, веса ш) 2  E ← множество ребер грамм  3  если | E | = 1 тогда возвращаться E еще 4      А ← полуребра в E чей вес не меньше среднего веса 5 B ← E - А 6      F ← лес граммB 7      если F это остовное дерево тогда 8          возвращаться MBST (граммB,ш) 9      еще 10         возвращаться MBST ((граммА)η, ш) ${\displaystyle \cup }$ F

В приведенном выше (грамм_А)_η - подграф, составленный из супервершин (считая вершины несвязного компонента за единицу) и ребер в А.

Продолжительность

Алгоритм работает в О (E) время, где E количество ребер. Эта оценка достигается следующим образом:

• разделение на два набора с помощью алгоритмов нахождения медианы в О(E)
• найти лес в О(E)
• учитывая половину ребер в E на каждой итерации О(E + E/2 + E/4 + ··· + 1) = О(E)

Пример

В следующем примере зеленые края используются для формирования MBST, а пунктирные красные области обозначают супервершины, сформированные на этапах алгоритма.

	Алгоритм делит ребра наполовину на два набора по весам. Зеленые ребра - это те ребра, вес которых минимален.
	Поскольку в подграфе есть остовное дерево, состоящее только из ребер меньшего набора. Повторите поиск MBST в этом подграфе.
	Поскольку в текущем подграфе нет остовного дерева, образованного ребрами в текущем наборе меньших ребер. Объедините вершины отключенного компонента с супервершиной (обозначенной пунктирной красной областью), а затем найдите MBST в подграфе, образованном супервершинами и ребрами в наборе больших ребер. Лес, сформированный внутри каждого отключенного компонента, будет частью MBST в исходном графе.
	Повторите аналогичные шаги, объединив больше вершин в супервершину.
	Наконец, алгоритм получает MBST, используя ребра, найденные во время алгоритма.

Алгоритмы MBSA для ориентированных графов

Для ориентированного графа доступны два алгоритма: алгоритм Камерини для поиска MBSA и алгоритм Габова и Тарьяна.^[4]

Алгоритм Камерини для MBSA

Для ориентированного графа алгоритм Камерини фокусируется на поиске набора ребер, которые будут иметь максимальную стоимость как узкое место стоимости MBSA. Это делается путем разбиения множества ребер E на два набора А и B и поддерживая набор Т это набор, в котором известно, что грамм_Т не имеет протяженного дерева, увеличивая Т к B всякий раз, когда максимальное древообразование грамм(B ∪ Т) не является продолжающимся древовидным грамм, иначе уменьшаем E кА. Общая временная сложность составляет О(E бревноE).^[5][4]

Псевдокод

функция MBSA (грамм, ш, Т) является    E ← множество ребер грамм     если | E - T | > 1 тогда        А ← UH (E-T) B ← (E - T) − А        F ← БУШ (граммНО)        если F остовное древообразование G тогда            S ← F MBSA ((граммНО), ш, Т)        еще            MBSA (G, ш, ВАННА);

1. T представляет собой подмножество E, для которого известно, что G_Т не содержит никакого остовного древовидного происхождения с корнем в узле «а». Изначально T пусто
2. UH берет (E − T) набор ребер в G и возвращает A ⊂ (E − T) такое, что:
   1. ${\displaystyle |A|=\left\lfloor {\frac {(|E-T|)}{2}}\right\rfloor }$
   2. W_а ≥ Вт_б , для a ∈ A и b ∈ B
3. BUSH (G) возвращает максимальное древообразование G с корнем в узле «а»
4. Конечный результат будет S

Пример

	После запуска первой итерации этого алгоритма мы получаем F и F не является растяжением грамм, Итак, запускаем код ${\displaystyle MBSA(G,w,T\cup B).}$
	Во второй итерации мы получаем ${\displaystyle F'}$ и ${\displaystyle F'}$ также не является растяжением грамм, Итак, запускаем код ${\displaystyle MBSA(G,w,T'\cup B')}$
	На третьей итерации получаем ${\displaystyle F''}$ и ${\displaystyle F''}$ это обширное древо грамм, Итак, запускаем код ${\displaystyle MBSA(G_{T''\cup B''},w,T'')}$
	когда мы запускаем ${\displaystyle MBSA(G_{T''\cup B''},w,T'')}$, то ${\displaystyle |E-T|}$ равно 1, что не больше 1, поэтому алгоритм возвращает и окончательный результат ${\displaystyle S=F''}$.

Алгоритм Габоу и Тарьяна для MBSA

Габов и Тарджан представили модификацию Алгоритм Дейкстры для кратчайшего пути с одним источником, который создает MBSA. Их алгоритм работает в О(E + V бревноV) время, если Куча Фибоначчи использовал.^[7]

Псевдокод

 Для графика G (V, E), F это набор вершин в V. Первоначально, F = {s} куда s это начальная точка графика грамм и c(s) = -∞ 1  функция МБСА-ГТ (грамм, ш, т) 2      повторение | V | раз 3 Выбрать v с минимумом c(v) из F; 4 Удалите его из F; 5          за ∀ край (v, w) делать 6              если ш ∉ F или ∉ Дерево тогда 7 добавить ш к F;           8                  c(ш) = c(v, w); 9                  п(ш) = v;      10             еще 11                 если ш ∈ F и с (ш)> с (v, ш) тогда 12                     c(ш) = c(v, w); 13                     п(ш) = v;

Пример

Следующий пример показывает, как работает алгоритм.

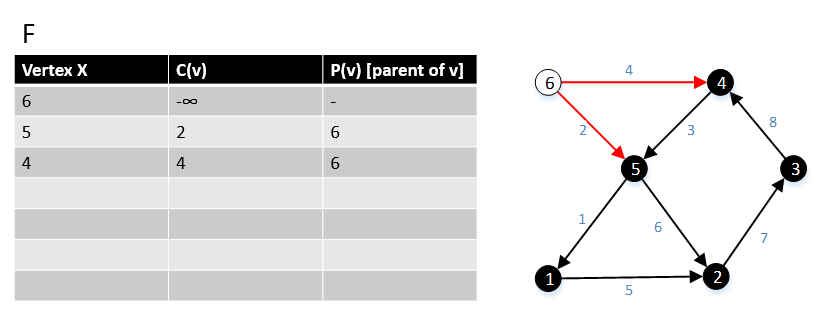На первом шаге алгоритма мы выбираем корень s из графа G, на рисунке выше вершина 6 является корнем s. Затем мы нашли все ребра (6, w) ∈ E и их стоимость c (6, w), где w ∈ V.

Далее переходим к вершине 5 в графе G, мы нашли все ребра (5, w) ∈ E и их стоимость c (5, w), где w ∈ V.

Далее переходим к вершине 4 в графе G, мы нашли все ребра (4, w) ∈ E и их стоимость c (4, w), где w ∈ V. Находим, что ребро (4,5)> край (6.5), поэтому оставим край (6,5) и удалим край (4,5).

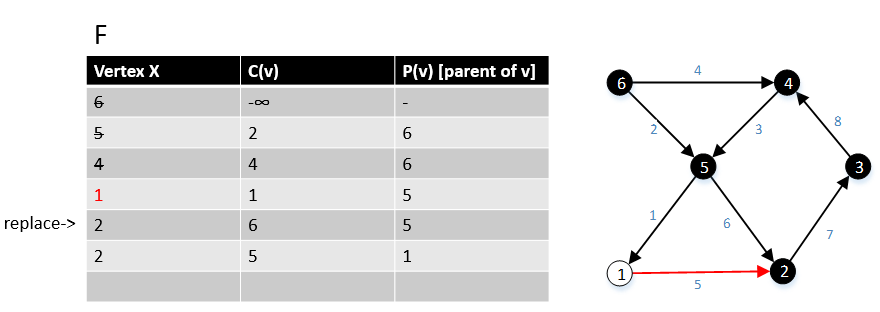Далее переходим к вершине 1 в графе G, мы нашли все ребра (1, w) ∈ E и их стоимость c (1, w), где w ∈ V. Находим, что ребро (5,2)> край (1,2), поэтому мы удалим край (5,2) и оставим край (1,2).

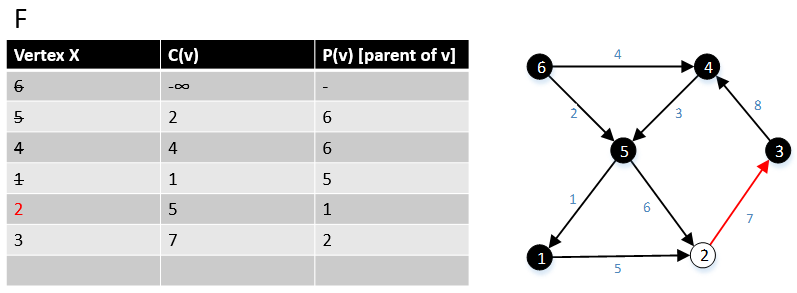Далее переходим к вершине 2 в графе G, мы нашли все ребра (2, w) ∈ E и их стоимость c (2, w), где w ∈ V.

Далее переходим к вершине 3 в графе G, мы нашли все ребра (3, w) ∈ E и их стоимость c (3, w), где w ∈ V. Мы находим, что ребро (3,4)> край (6,4), поэтому мы удалим край (3,4) и оставим край (6,4).

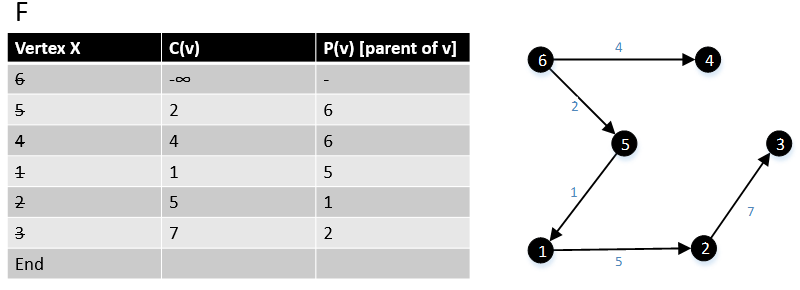После того, как мы перебрали все вершины в графе G, алгоритм завершился.

Другой подход, предложенный Тарььяном и Габоу с оценкой О(E бревно^* V) для разреженных графов, в которых он очень похож на алгоритм Камерини для MBSA, но вместо разделения набора ребер на два набора на каждой итерации, K(я) был представлен, в котором я - это количество имевших место разбиений или, другими словами, номер итерации, и K(я) - возрастающая функция, обозначающая количество секционированных наборов, которые необходимо иметь на итерацию. K(я) = 2^{k(я − 1)} с k(1) = 2. Алгоритм находит λ^* в котором это значение узкого места в любом MBSA. После λ^* обнаружено какое-либо протяженное древообразование в грамм(λ^*) это MBSA, в котором грамм(λ^*) это граф, в котором стоимость всех его ребер равна ≤ λ^*.^[4][7]

Рекомендации

1. Все о связующем дереве по узким местам
2. Мурали, Т. М. (2009), Применение минимальных остовных деревьев (PDF)
3. в вопросе 3 у вас есть доказательство этого утверждения (PDF)
4. Трабулси, Ахмад (2014), Узкие места, соединяющие деревья (PDF), заархивировано из оригинал (PDF) на 2016-03-04, получено 2014-12-28
5. Камерини, П. (1978), «Проблема минимального и максимального остовного дерева и некоторые расширения», Письма об обработке информации, 7 (1): 10, Дои:10.1016/0020-0190(78)90030-3
6. Цуй, Юйсян (2013), Остовное дерево с минимальным узким местом (PDF), заархивировано из оригинал (PDF) на 2016-03-04, получено 2014-12-28
7. Габоу, Гарольд Н.; Тарджан, Роберт Э (1988). «Алгоритмы для двух задач оптимизации узких мест». Журнал алгоритмов. 9 (3): 411–417. Дои:10.1016/0196-6774(88)90031-4. ISSN  0196-6774.