Радиальная скорость - Radial velocity

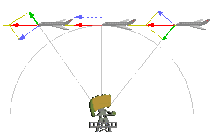
"Радиальная скорость" перенаправляется сюда. Не следует путать с радиальное движение.
Самолет, пролетающий мимо радиолокационной станции: вектор скорости самолета (красный) представляет собой сумму радиальной скорости (зеленый цвет) и тангенциальной скорости (синий цвет).

В радиальная скорость объекта по отношению к данной точке - это скорость изменения расстояния между объектом и точкой. То есть лучевая скорость является составляющей скорость который указывает в направлении радиуса, соединяющего точку и объект. В астрономии точкой обычно считается наблюдатель на Земле, поэтому радиальная скорость затем обозначает скорость, с которой объект удаляется от Земли (или приближается к ней при отрицательной радиальной скорости).

В астрономии лучевая скорость часто измеряется в первом приближении по формуле Доплеровская спектроскопия. Количество, полученное этим методом, можно назвать барицентрическая мера лучевой скорости или спектроскопическая лучевая скорость.[1] Однако из-за релятивистский и космологический Эффекты на больших расстояниях, на которые обычно распространяется свет, чтобы достичь наблюдателя от астрономического объекта, эта мера не может быть точно преобразована в геометрическую лучевую скорость без дополнительных предположений об объекте и пространстве между ним и наблюдателем.[2] Напротив, астрометрическая лучевая скорость определяется астрометрический наблюдения (например, светское изменение в ежегодном параллакс ).[2][3][4]

Спектроскопическая лучевая скорость

Свет от объекта со значительной относительной лучевой скоростью при испускании будет подвергаться воздействию Эффект Допплера, поэтому частота света уменьшается для удаляющихся (красное смещение ) и увеличивается для приближающихся объектов (синее смещение ).

Лучевая скорость звезда или другие светящиеся далекие объекты можно точно измерить, сделав снимок с высоким разрешением спектр и сравнивая измеренные длины волн известных спектральные линии до длин волн из лабораторных измерений. Положительная радиальная скорость указывает, что расстояние между объектами увеличивается или увеличивается; отрицательная лучевая скорость указывает, что расстояние между источником и наблюдателем уменьшается или уменьшается.

Уильям Хаггинс рискнул в 1868 году оценить радиальную скорость Сириус по отношению к Солнцу на основе наблюдаемого красного смещения света звезды. [5]

Диаграмма, показывающая, как орбита экзопланеты меняет положение и скорость звезды, когда они вращаются вокруг общего центра масс.

Во многих двойные звезды, то орбитальный движение обычно вызывает изменение лучевой скорости на несколько километров в секунду (км / с). Поскольку спектры этих звезд меняются из-за эффекта Доплера, их называют спектроскопические двойные системы. Радиальную скорость можно использовать для оценки соотношения масс звезд, а некоторые орбитальные элементы, Такие как эксцентриситет и большая полуось. Тот же метод был использован для обнаружения планеты вокруг звезд таким образом, что измерение движения определяет период обращения планеты, в то время как результирующая лучевая скорость амплитуда позволяет вычислить нижнюю границу планетарного масса с использованием бинарная функция масс. Одни только методы радиальной скорости могут выявить только нижнюю границу, поскольку большая планета, вращающаяся под очень большим углом к ​​лучу зрения, будет возмущать свою звезду в радиальном направлении так же, как гораздо меньшая планета с орбитальной плоскостью на луче зрения. Было высказано предположение, что планеты с высокими эксцентриситетами, рассчитанными этим методом, на самом деле могут быть двухпланетными системами с круговой или почти круговой резонансной орбитой.[6][7]

Обнаружение экзопланет

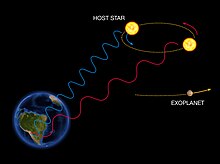
Основная статья: Доплеровская спектроскопия
Метод лучевых скоростей для обнаружения экзопланет

Метод лучевых скоростей для обнаружения экзопланеты основан на обнаружении изменений скорости центральной звезды из-за изменения направления гравитационного притяжения от (невидимой) экзопланеты, когда она вращается вокруг звезды. Когда звезда движется к нам, ее спектр смещается в синюю сторону, а когда она удаляется от нас, она смещается в красную сторону. Регулярно просматривая спектр звезды - и, следовательно, измеряя ее скорость - можно определить, движется ли она периодически из-за влияния спутника-экзопланеты.

Сжатие данных

С инструментальной точки зрения скорости измеряются относительно движения телескопа. Итак, важный первый шаг сжатие данных состоит в том, чтобы удалить вклады

Смотрите также

Рекомендации

  1. ^ Разрешение C1 по определению спектроскопической «барицентрической меры радиальной скорости». Специальный выпуск: Предварительная программа XXV Генеральной Ассамблеи в Сиднее, 13–26 июля 2003 г. Информационный бюллетень № 91. Стр. 50. Секретариат МАС. Июль 2002 г. https://www.iau.org/static/publications/IB91.pdf
  2. ^ а б Линдегрен, Леннарт; Дравинс, Дайнис (апрель 2003 г.). "Основное определение" лучевой скорости"" (PDF). Астрономия и астрофизика. 401 (3): 1185–1201. arXiv:Astro-ph / 0302522. Bibcode:2003A&A ... 401.1185L. Дои:10.1051/0004-6361:20030181. Получено 4 февраля 2017.
  3. ^ Дравинс, Дайнис; Линдегрен, Леннарт; Мадсен, Сорен (1999). «Астрометрические лучевые скорости. I. Неспектроскопические методы измерения лучевой скорости звезд». Astron. Астрофизики. 348: 1040–1051. arXiv:Astro-ph / 9907145. Bibcode:1999 А и А ... 348.1040D.
  4. ^ Резолюция C 2 по определению «астрометрической радиальной скорости». Специальный выпуск: Предварительная программа XXV Генеральной Ассамблеи в Сиднее, 13–26 июля 2003 г. Информационный бюллетень № 91. Стр. 51. Секретариат МАС. Июль 2002 г. https://www.iau.org/static/publications/IB91.pdf
  5. ^ Хаггинс, В. (1868). «Дальнейшие наблюдения за спектрами некоторых звезд и туманностей с попыткой определить по ним, движутся ли эти тела к Земле или от Земли, а также наблюдения за спектрами Солнца и Кометы II». Философские труды Лондонского королевского общества. 158: 529–564. Bibcode:1868РСПТ..158..529Х. Дои:10.1098 / рстл.1868.0022.
  6. ^ Англада-Эскуд, Гиллем; Лопес-Моралес, Мерседес; Чемберс, Джон Э. (2010). «Как эксцентричные орбитальные решения могут скрыть планетные системы на резонансных орбитах 2: 1». Письма в астрофизический журнал. 709 (1): 168–78. arXiv:0809.1275. Bibcode:2010ApJ ... 709..168A. Дои:10.1088 / 0004-637X / 709/1/168.
  7. ^ Кюрстер, Мартин; Трифонов, Трифон; Рефферт, Сабина; Костогрыз, Надия М .; Родер, Флориан (2015). "Отделение резонансных отверстий лучевой скорости 2: 1 от эксцентрических и пример HD 27894". Astron. Астрофизики. 577: A103. arXiv:1503.07769. Bibcode:2015 A&A ... 577A.103K. Дои:10.1051/0004-6361/201525872.
  8. ^ Ferraz-Mello, S .; Мичченко, Т.А. (2005). «Внесолнечные планетные системы». Лект. Нет. Phys. 683. С. 219–271. Bibcode:2005ЛНП ... 683..219Ф. Дои:10.1007/10978337_4.
  9. ^ Reid, M. J .; Дам, Т. М. (2016). «О скорости вращения Млечного Пути, определенной по излучению HI». Астрофизический журнал. 832 (2): 159. arXiv:1608.03886. Bibcode:2016ApJ ... 832..159R. Дои:10.3847 / 0004-637X / 832/2/159.
  10. ^ Штумпфф, П. (1985). «Строгая трактовка гелиоцентрического движения звезд». Astron. Астрофизики. 144 (1): 232. Bibcode:1985A & A ... 144..232S.