Метод Ромберга - Rombergs method - Wikipedia

В числовой анализ, Метод Ромберга (Ромберг 1955 ) используется для оценки определенный интеграл

{ displaystyle int _ {a} ^ {b} f (x) , dx}

применяя Экстраполяция Ричардсона (Ричардсон 1911 ) неоднократно на правило трапеции или правило прямоугольника (правило средней точки). Оценки дают треугольная решетка. Метод Ромберга - это Формула Ньютона – Котеса - он вычисляет подынтегральное выражение в точках, расположенных на одинаковом расстоянии. Подынтегральное выражение должно иметь непрерывные производные, хотя неплохие результаты могут быть получены, если существует только несколько производных. Если возможно вычислить подынтегральное выражение в точках, разнесенных на неравные расстояния, тогда используйте другие методы, такие как Квадратура Гаусса и Квадратура Кленшоу – Кертиса обычно более точны.

Метод назван в честь Вернер Ромберг (1909–2003), которые опубликовали метод в 1955 году.

Метод

С помощью

{ displaystyle h_ {n} = { tfrac {1} {2 ^ {n}}} (b-a)}

метод может быть индуктивно определен как

{ Displaystyle R (0,0) = h_ {1} (f (a) + f (b))}

{ Displaystyle R (n, 0) = { tfrac {1} {2}} R (n-1,0) + h_ {n} sum _ {k = 1} ^ {2 ^ {n-1} } f (a + (2k-1) h_ {n})}

{ Displaystyle R (n, m) = R (n, m-1) + { tfrac {1} {4 ^ {m} -1}} (R (n, m-1) -R (n-1) , м-1))}

или же

{ Displaystyle R (n, m) = { tfrac {1} {4 ^ {m} -1}} (4 ^ {m} R (n, m-1) -R (n-1, m-1) ))}

куда ${ Displaystyle п geq м ,}$ и ${ Displaystyle м geq 1 ,}$ . В нотация большой O, ошибка для р(п, м) является (Мысовских 2002 ):

{ displaystyle O left (h_ {n} ^ {2m + 2} right). ,}

Нулевая экстраполяция, р(п, 0), эквивалентно трапеция с 2^п + 1 балл; первая экстраполяция, р(п, 1), эквивалентно Правило Симпсона с 2^п +1 балл. Вторая экстраполяция, р(п, 2), эквивалентно Правило Буля с 2^п +1 балл. Дальнейшие экстраполяции отличаются от формул Ньютона-Котеса. В частности, дальнейшие экстраполяции Ромберга очень незначительно расширяют правило Буля, изменяя веса в отношения, аналогичные тем, которые используются в правиле Буля. Напротив, дальнейшие методы Ньютона-Котеса дают все более разные веса, что в конечном итоге приводит к большим положительным и отрицательным весам. Это свидетельствует о том, что методы полинома Ньютона-Котеса с большой степенью интерполяции не могут сходиться для многих интегралов, в то время как интегрирование Ромберга более стабильно.

Когда оценки функций дороги, может быть предпочтительнее заменить полиномиальную интерполяцию Ричардсона рациональной интерполяцией, предложенной Булирш и Стоер (1967).

Геометрический пример

Чтобы оценить площадь под кривой, правило трапеций применяется сначала к цельному элементу, затем к двум, затем к четырем и так далее.

Один кусочек. Обратите внимание, поскольку оно начинается и заканчивается на нуле, это приближение дает нулевую площадь.

Два куска

Из четырех частей

Восемь частей

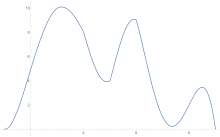
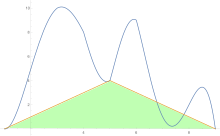
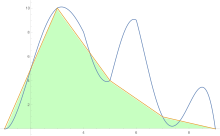
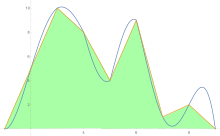
После получения оценок по правилу трапеций Экстраполяция Ричардсона применяется.

Для первой итерации в формуле используются двухчастные и однократные оценки (4 × (более точный) - (менее точный)) / 3 Затем та же формула используется для сравнения оценки из четырех и двух частей, а также для более высоких оценок.
Для второй итерации значения первой итерации используются в формуле (16 (более точный) - менее точный)) / 15
Третья итерация использует следующую степень 4: (64 (более точно) - менее точно)) / 63 от значений, полученных на второй итерации.
Схема продолжается до тех пор, пока не будет одна оценка.

Количество штук	Оценки трапеции	Первая итерация	Вторая итерация	Третья итерация
		(4 MA - LA) / 3 *	(16 MA - LA) / 15	(64 MA - LA) / 63
1	0	(4×16 − 0)/3 = 21.333...	(16×34.667 − 21.333)/15 = 35.556...	(64×42.489 − 35.556)/63 = 42.599...
2	16	(4×30 − 16)/3 = 34.666...	(16×42 − 34.667)/15 = 42.489...
4	30	(4×39 − 30)/3 = 42
8	39

MA означает более точный, LA означает менее точный

Пример

Например, Функция Гаусса интегрируется от 0 до 1, т.е. функция ошибки erf (1) ≈ 0,842700792949715. Треугольный массив вычисляется построчно, и вычисление прекращается, если две последние записи в последней строке отличаются менее чем на 10.⁻⁸.

 0.77174333 0.82526296  0.84310283 0.83836778  0.84273605  0.84271160 0.84161922  0.84270304  0.84270083  0.84270066 0.84243051  0.84270093  0.84270079  0.84270079  0.84270079

Результат в правом нижнем углу треугольного массива соответствует показанным цифрам. Примечательно, что этот результат получен из менее точных приближений, полученных с помощью правила трапеции в первом столбце треугольного массива.

Выполнение

Вот пример компьютерной реализации метода Ромберга (в Язык программирования C ).

#включают <stdio.h>#включают <math.h>пустотаdump_row(size_t я, двойной *р) {   printf("R [% 2zu] =", я);   за (size_t j = 0; j <= я; ++j){      printf("% f", р[j]);   }   printf(" п");}двойнойRomberg(двойной (*ж/ * функция для интеграции * /)(двойной), двойной /*Нижний предел*/ а, двойной /*верхний предел*/ б, size_t max_steps, двойной / * желаемая точность * / соотв) {   двойной R1[max_steps], R2[max_steps]; // буферы   двойной *Rp = &R1[0], *Rc = &R2[0]; // Rp - предыдущая строка, Rc - текущая строка   двойной час = (б-а); //размер шага   Rp[0] = (ж(а) + ж(б))*час*.5; // первый шаг трапеции   dump_row(0, Rp);   за (size_t я = 1; я < max_steps; ++я) {      час /= 2.;      двойной c = 0;      size_t ep = 1 << (я-1); // 2 ^ (n-1)      за (size_t j = 1; j <= ep; ++j) {         c += ж(а+(2*j-1)*час);      }      Rc[0] = час*c + .5*Rp[0]; // R (i, 0)      за (size_t j = 1; j <= я; ++j) {         двойной н_к = пау(4, j);         Rc[j] = (н_к*Rc[j-1] - Rp[j-1])/(н_к-1); // вычисляем R (i, j)      }      // Дамп i-го столбца R, R [i, i] - лучшая оценка на данный момент      dump_row(я, Rc);      если (я > 1 && фабрики(Rp[я-1]-Rc[я]) < соотв) {         возвращаться Rc[я-1];      }      // меняем местами Rn и Rc, так как нам нужна только последняя строка      двойной *rt = Rp;      Rp = Rc;      Rc = rt;   }   возвращаться Rp[max_steps-1]; // возвращаем наше лучшее предположение}

внешняя ссылка

ROMBINT - код для MATLAB (автор: Мартин Каценак)
Бесплатный онлайн-инструмент интеграции с использованием методов Ромберга, Фокса – Ромберга, Гаусса – Лежандра и других численных методов.
SciPy реализация метода Ромберга