Сиамский метод - Siamese method

Простой пример сиамского метода. Начиная с «1» квадраты заполняются по диагонали вверх и вправо (↗). Когда ход покидает квадрат, он переносится в последнюю строку или первый столбец соответственно. Если встречается заполненный прямоугольник, вместо этого нужно перемещаться по вертикали на один прямоугольник (↓), а затем продолжать, как раньше.

В Сиамский метод, или Метод де ла Лубера, это простой метод создания любого размера п-странный магические квадраты (т.е. числовые квадраты, в которых суммы всех строк, столбцов и диагоналей идентичны). Метод был доведен до Франция в 1688 г. французами математик и дипломат Симон де ла Лубер,^[1] когда он возвращался из своего посольства 1687 года в королевство Сиам.^[2]^[3]^[4] Сиамский метод позволяет создавать магические квадраты просто.

Публикация

Описание сиамского метода в Симон де ла Лубер 1693 г. Новое историческое отношение королевства Сиам.

Де ла Лубер опубликовал свои открытия в своей книге. Новое историческое отношение королевства Сиам (Du Royaume de Siam, 1693), в главе, озаглавленной Проблема магического квадрата по мнению индейцев.^[5]Хотя этот метод обычно квалифицируется как «сиамский», что относится к путешествию де ла Лубера в страну Сиама, сам де ла Лубер узнал его от француза по имени Винсент (врач, который впервые побывал в Сиаме). Персия а затем в Сиам, и возвращался во Францию с посольством де ла Лубера), который сам научился этому в городе Сурат в Индия:^[5]

"Мистер Винсент, о котором я так часто упоминал в своих связиувидев меня однажды на корабле, во время нашего возвращения, я старательно расставляю Магические квадраты, следуя методу Bachet, сообщил мне, что Индейцы из Суратте расставил их с гораздо большей легкостью и научил меня их методу только для неравных квадратов, забыв, как он сказал, метод равных "
— Симон де ла Лубер, Новое историческое отношение королевства Сиам.^[5]

Метод

Метод удивил своей эффективностью и простотой:

«Я надеюсь, что будет приемлемым то, что я приведу правила и продемонстрирую этот метод, который удивителен своей исключительной легкостью в реализации того, что показалось нашим математикам трудным»
— Симон де ла Лубер, Новое историческое отношение королевства Сиам.^[5]

Во-первых, арифметическая прогрессия должен быть выбран (например, простая прогрессия 1,2,3,4,5,6,7,8,9 для квадрата с тремя строками и столбцами ( Площадь Ло Шу )).

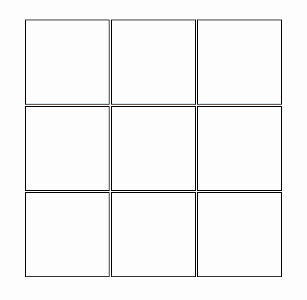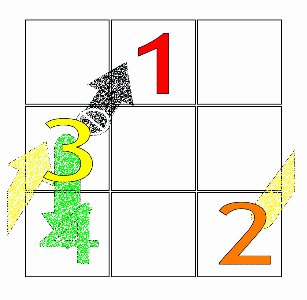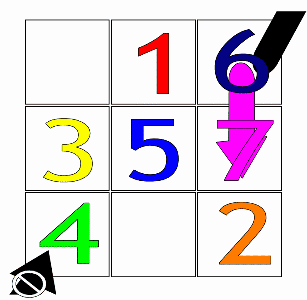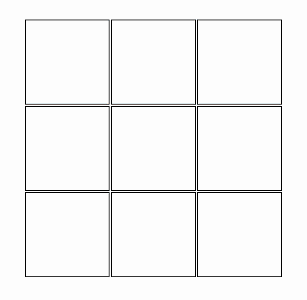
Затем, начиная с центрального квадрата первого ряда с цифрой 1 (или первым числом любой арифметической прогрессии), основное движение для заполнения ячеек происходит по диагонали. вверх и вправо (↗), один шаг за раз. Когда ход покидает квадрат, он переносится в последнюю строку или первый столбец соответственно.

Если встречается заполненный прямоугольник, перемещается вертикально вниз на одну коробку (↓), а затем продолжайте как раньше.

Магические квадраты порядка 3

шаг 1
	1
	.
	.

шаг 2
	1
	.
		2

шаг 3
	1
3
		2

шаг 4
	1
3
4		2

шаг 5
	1
3	5
4		2

шаг 6
	1	6
3	5
4		2

шаг 7
	1	6
3	5	7
4		2

шаг 8
8	1	6
3	5	7
4		2

шаг 9
8	1	6
3	5	7
4	9	2

Магические квадраты порядка 5

Шаг 1
		1
		.
		.
		.
		.


1
.
.
.		3
.	2

Шаг 3
		1
	5
4		.
				3
			2

Шаг 4
		1	8
	5	7
4	6	.
				3
			2

Шаг 5
		1	8	15
	5	7	14
4	6	13
10	12			3
11			2	9

Шаг 6
17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

Другие размеры

Любые п-нечетный квадрат ("странный -order square ") может быть таким образом встроен в магический квадрат. Однако сиамский метод не работает для n-четных квадратов ("даже -упорядочить квадраты ", например, 2 строки / 2 столбца, 4 строки / 4 столбца и т. д. ...).

Заказ 3
8	1	6
3	5	7
4	9	2

Заказ 5
17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

Заказ 9
47	58	69	80	1	12	23	34	45
57	68	79	9	11	22	33	44	46
67	78	8	10	21	32	43	54	56
77	7	18	20	31	42	53	55	66
6	17	19	30	41	52	63	65	76
16	27	29	40	51	62	64	75	5
26	28	39	50	61	72	74	4	15
36	38	49	60	71	73	3	14	25
37	48	59	70	81	2	13	24	35

Прочие ценности

Может использоваться любая последовательность чисел при условии, что они образуют арифметическая прогрессия (т.е. разность любых двух последовательных членов последовательности постоянна). Также возможен любой стартовый номер. Например, следующая последовательность может быть использована для формирования магического квадрата 3-го порядка по сиамскому методу (9 блоков): 5, 10, 15, 20, 25, 30, 35, 40, 45 (магическая сумма дает 75, для все строки, столбцы и диагонали).

Заказ 3
40	5	30
15	25	35
20	45	10

Другие отправные точки

Можно не начинать арифметическую прогрессию с середины верхней строки, но тогда только суммы строк и столбцов будут идентичны и приведут к магической сумме, тогда как диагональные суммы будут отличаться. Таким образом, результат не будет настоящим магическим квадратом:

Заказ 3
500	700	300
900	200	400
100	600	800

Вращения и отражения

Множество других магических квадратов можно вывести из вышесказанного простым вращения и размышления.

Вариации

Существует несколько более сложный вариант этого метода, в котором первое число помещается в поле чуть выше центрального поля. Основное движение для наполнения ящиков остается вверх и вправо (↗), один шаг за раз. Однако, если встречается заполненный прямоугольник, он перемещается вертикально. две коробки вместо этого, продолжая как раньше.

Заказ 5
23	6	19	2	15
10	18	1	14	22
17	5	13	21	9
4	12	25	8	16
11	24	7	20	3

Многочисленные варианты могут быть получены простым поворотом и отражением. Следующий квадрат эквивалентен приведенному выше (простое отражение): первое число помещается в прямоугольник чуть ниже центрального квадрата. Основное движение для заполнения ящиков тогда становится диагональным. вниз и вправо (↘), один шаг за раз. Если встречается заполненный прямоугольник, перемещается вертикально вниз две коробки вместо этого, продолжая как раньше.^[6]

Заказ 5
11	24	7	20	3
4	12	25	8	16
17	5	13	21	9
10	18	1	14	22
23	6	19	2	15

Эти вариации, хотя и не так просты, как основной сиамский метод, эквивалентны методам, разработанным более ранними арабскими и европейскими учеными, такими как Мануэль Москопулос (1315), Иоганн Фаульхабер (1580–1635) и Клод Гаспар Баше де Мезириак (1581–1638) и позволяли создавать магические квадраты, подобные их.^[6]^[7]

Было обнаружено^[8]^[9]^[10]^[11]^[12] что размещение начального номера один для порядка> 5 не ограничивается первыми или соседними по центру рядами. Было обнаружено, что число один может быть помещено в любую из ячеек выше или ниже центрального блока, так что количество произведенных квадратов больше не 2, а n-1 для всего среднего столбца, где n - порядок. Величина вертикального перемещения (v.m.) определяется с помощью правила последовательных четных чисел, где v.m. равно 2 для ячеек, прилегающих к центральному блоку, и увеличивается на два, поскольку числовая единица располагается дальше от центрального блока по направлению к периферии (т. принимает значение n-1. Более того, количество квадратов простого порядка больше, чем квадратов составного порядка.

Вдобавок, Loubère больше не магия ниже центральной коробки ни для простого порядка, ни для составного порядка. Показаны шесть квадратов, которые могут быть созданы для группы порядка 7. Квадрат 6 - единственный не магический квадрат в группе.

Магические квадраты порядка 7

Квадрат 1
30	39	48	1	10	19	28
38	47	7	9	18	27	29
46	6	8	17	26	35	37
5	14	16	25	34	36	45
13	15	24	33	42	44	4
21	23	32	41	43	3	12
22	31	40	49	2	11	20

Квадрат 2
13	47	35	17	2	36	28
46	31	16	1	42	27	12
30	15	7	41	26	11	45
21	6	40	25	10	44	29
5	39	24	9	43	35	20
38	23	8	49	34	19	4
22	14	48	33	18	3	37

Квадрат 3
46	15	40	9	34	3	28
21	39	8	33	2	27	45
38	14	32	1	26	44	20
13	31	7	25	43	19	37
30	6	24	49	18	36	12
5	23	48	17	42	11	29
22	47	16	41	10	35	4

Квадрат 4
5	31	8	41	18	44	28
30	14	40	17	43	27	4
13	39	16	49	26	3	29
38	15	48	25	2	35	12
21	47	24	1	34	11	37
46	23	7	33	10	36	20
22	6	32	9	42	19	45

Квадрат 5
38	6	16	33	43	11	28
5	15	32	49	10	27	37
21	31	48	9	26	36	4
30	47	8	25	32	3	20
46	14	24	41	2	19	29
13	23	40	1	18	35	45
22	39	7	17	34	44	12

Квадрат 6
21	14	7	49	42	35	28
13	6	48	41	34	27	20
5	47	40	33	26	19	12
46	39	32	25	18	11	4
38	31	24	17	10	3	45
30	23	16	9	2	44	37
22	15	8	1	43	36	29

Смотрите также

Примечания и ссылки

^ Хиггинс, Питер (2008). История чисел: от счета к криптографии. Нью-Йорк: Коперник. п.54. ISBN 978-1-84800-000-1. сноска 8
^ Математические круги в квадрате "Филлип Э. Джонсон, Говард Уитли Ивс, стр. 22
^ CRC Краткая энциклопедия математики Эрик В. Вайсштейн, стр. 1839 [1]
^ Дзен магических квадратов, кругов и звезд Клиффорд А. Пиковер Страница 38 [2]
^ ^а ^б ^c ^d Новое историческое отношение королевства Сиам стр.228
^ ^а ^б Новое историческое отношение королевства Сиам p229
^ Дзен магических квадратов, кругов и звезд Клиффорд А. Пиковер, 2002, стр.37. [3]
^ oddwheel.com/meziriacnew.html
^ oddwheel.com/meziriacnew2.html
^ oddwheel.com/meziriacnew3.html
^ oddwheel.com/meziriacnew4.html
^ oddwheel.com/meziriacnew5.html

[1] Хиггинс, Питер (2008). История чисел: от счета к криптографии. Нью-Йорк: Коперник. п.54. ISBN 978-1-84800-000-1. сноска 8

[2] Математические круги в квадрате "Филлип Э. Джонсон, Говард Уитли Ивс, стр. 22

[3] CRC Краткая энциклопедия математики Эрик В. Вайсштейн, стр. 1839 [1]

[4] Дзен магических квадратов, кругов и звезд Клиффорд А. Пиковер Страница 38 [2]

[p228-5] а ^б ^c ^d Новое историческое отношение королевства Сиам стр.228

[p229-6] а ^б Новое историческое отношение королевства Сиам p229

[7] Дзен магических квадратов, кругов и звезд Клиффорд А. Пиковер, 2002, стр.37. [3]

[8] wheel.com/meziriacnew.html

[9] wheel.com/meziriacnew2.html

[10] wheel.com/meziriacnew3.html

[11] wheel.com/meziriacnew4.html

[12] wheel.com/meziriacnew5.html

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]