В метод отклонения откоса это структурный анализ метод для балки и кадры введен в 1914 году Джорджем А. Мани.[1] Метод отклонения откоса широко использовался более десяти лет, пока метод распределения моментов был развит. В книге «Теория и практика современных каркасных структур», написанной Дж. Б. Джонсоном, К. У. Брайаном и Ф. Э. Турнеором, утверждается, что этот метод был впервые разработан «профессором Отто Мором в Германии, а затем независимо разработан профессором Г.А. Мани ». Согласно этой книге, профессор Отто Мор впервые представил этот метод в своей книге «Оценка ферм с жесткими узловыми соединениями» или «Die Berechnung der Fachwerke mit Starren Knotenverbindungen».
Вступление
Формируя уравнения отклонения откоса и применяя условия равновесия соединения и сдвига, вычисляются углы поворота (или углы наклона). Подставляя их обратно в уравнения отклонения откоса, можно легко определить конечные моменты стержня. Деформация элемента происходит из-за изгибающего момента.
Уравнения отклонения откоса
Уравнения прогиба склона также можно записать с использованием коэффициента жесткости  и вращение хорды
и вращение хорды  :
:
Вывод уравнений прогиба откоса
Когда простой луч длины  и жесткость на изгиб
и жесткость на изгиб  нагружается на каждом конце с моментами по часовой стрелке
нагружается на каждом конце с моментами по часовой стрелке  и
и  , торцевые повороты стержня происходят в том же направлении. Эти углы поворота можно рассчитать с помощью метод единичной силы или закон Дарси.
, торцевые повороты стержня происходят в том же направлении. Эти углы поворота можно рассчитать с помощью метод единичной силы или закон Дарси.


Переставляя эти уравнения, выводятся уравнения отклонения откоса.
Условия равновесия
Совместное равновесие
Условия совместного равновесия подразумевают, что каждое сочленение со степенью свободы не должно иметь неуравновешенных моментов, то есть быть в равновесии. Следовательно,

Здесь,  конечные моменты члена,
конечные моменты члена,  являются фиксированные конечные моменты, и
являются фиксированные конечные моменты, и  внешние моменты, непосредственно приложенные к соединению.
внешние моменты, непосредственно приложенные к соединению.
Равновесие сдвига
При поворотах хорды в раме необходимо учитывать дополнительные условия равновесия, а именно условия равновесия сдвига.
Пример
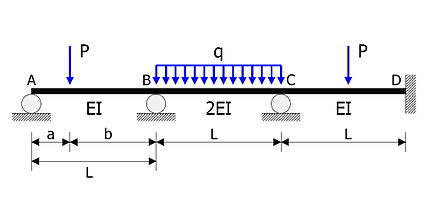
Пример
Статически неопределимая балка, показанная на рисунке, подлежит анализу.
- Элементы AB, BC, CD имеют одинаковую длину.
 .
. - Жесткости при изгибе равны EI, 2EI, EI соответственно.
- Концентрированная нагрузка величины
 действует на расстоянии
действует на расстоянии  от опоры А.
от опоры А. - Равномерная нагрузка по интенсивности
 действует на BC.
действует на BC. - Компонент CD загружен в середине пролета концентрированной нагрузкой величины
 .
.
В следующих расчетах моменты и вращения по часовой стрелке положительны.
Степени свободы
Углы поворота  ,
,  ,
,  , соединений A, B, C, соответственно, принимаются за неизвестные. Повороты хорды отсутствуют по другим причинам, включая оседание опоры.
, соединений A, B, C, соответственно, принимаются за неизвестные. Повороты хорды отсутствуют по другим причинам, включая оседание опоры.
Фиксированные конечные моменты
Фиксированные конечные моменты:






Уравнения отклонения откоса
Уравнения отклонения откоса строятся следующим образом:






Совместные уравнения равновесия
Соединения A, B, C должны удовлетворять условию равновесия. Следовательно



Углы поворота
Углы поворота вычисляются из одновременных уравнений выше.



Конечные моменты участника
Подстановка этих значений обратно в уравнения отклонения откоса дает конечные моменты стержня (в кНм):






Смотрите также
Примечания
- ^ Мани, Джордж А. (1915). «Исследования в области инженерии». Миннеаполис: Университет Миннесоты.
Рекомендации












































