Статическая форма однократного назначения - Static single assignment form
В компилятор дизайн, статическая форма единого назначения (часто сокращенно Форма SSA или просто SSA) является свойством промежуточное представление (IR), что требует, чтобы каждая переменная была назначен ровно один раз, и каждая переменная должна быть определена перед ее использованием. Существующие переменные в исходном IR разбиты на версии, новые переменные обычно обозначаются исходным именем с нижним индексом в учебниках, так что каждое определение получает свою собственную версию. В форме SSA, цепочки use-def являются явными и содержат один элемент.
SSA был предложен Барри К. Розен, Марк Н. Вегман, и Ф. Кеннет Задек в 1988 г.[1] Рон Ситрон, Жанна Ферранте и предыдущие три исследователя в IBM разработал алгоритм, который может эффективно вычислять форму SSA.[2]
Можно ожидать найти SSA в компиляторе для Фортран, C или C ++, тогда как в функциональный язык компиляторы, например, для Схема и ML, стиль передачи (CPS) обычно используется. SSA формально эквивалентен подмножеству CPS с хорошим поведением, за исключением нелокального потока управления, чего не происходит, когда CPS используется в качестве промежуточного представления.[3] Таким образом, оптимизации и преобразования, сформулированные в терминах одного, немедленно применяются к другому.
Льготы
Основная полезность SSA заключается в том, что он одновременно упрощает и улучшает результаты различных оптимизация компилятора, упрощая свойства переменных. Например, рассмотрим этот фрагмент кода:
у: = 1у: = 2х: = у
Люди могут видеть, что первое задание не обязательно и что значение у использование в третьей строке происходит от второго присвоения у. Программа должна была бы выполнять достижение анализа определения чтобы определить это. Но если программа имеет форму SSA, оба из них действуют немедленно:
у1 : = 1г2 : = 2x1 : = y2
Оптимизация компилятора алгоритмы, которые либо включены, либо сильно улучшены за счет использования SSA, включают:
- Постоянное распространение
- Распространение диапазона значений[4]
- Редкое распространение условных констант
- Устранение мертвого кода
- Нумерация глобальных значений
- Устранение частичной избыточности
- Снижение силы
- Размещение регистров
Переход на SSA
Преобразование обычного кода в форму SSA - это в первую очередь простой вопрос замены цели каждого присваивания новой переменной и замены каждого использования переменной «версией» переменной. достижение этот момент. Например, рассмотрим следующие граф потока управления:

Изменение имени в левой части "x" x - 3 "и изменив следующие варианты использования Икс с этим новым названием программа останется неизменной. Это можно использовать в SSA, создав две новые переменные: Икс1 и Икс2, каждый из которых назначается только один раз. Аналогичным образом, присвоение отличительных индексов всем другим переменным дает:
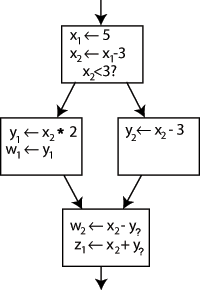
Понятно, к какому определению относится каждое использование, за исключением одного случая: оба использования у в нижнем блоке может относиться к любому у1 или у2, в зависимости от того, какой путь выбрал поток управления.
Чтобы решить эту проблему, в последний блок вставляется специальный оператор, называемый Функция Φ (Phi). Этот оператор создаст новое определение у называется у3 "выбирая" либо у1 или у2, в зависимости от потока управления в прошлом.
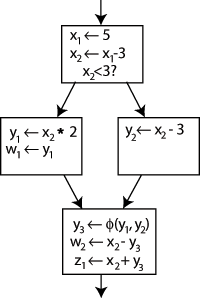
Теперь последний блок может просто использовать у3, и в любом случае будет получено правильное значение. Функция Φ для Икс не требуется: только одна версия Икс, а именно Икс2 достигает этого места, поэтому проблем нет (другими словами, Φ (Икс1,Икс2)=Икс2).
Учитывая произвольный граф потока управления, может быть трудно сказать, где вставить Φ-функции и для каких переменных. Этот общий вопрос имеет эффективное решение, которое может быть вычислено с использованием концепции, называемой границы господства (см. ниже).
Функции Φ не реализованы как машинные операции на большинстве машин. Компилятор может реализовать функцию Φ, вставляя операции «перемещения» в конец каждого предшествующего блока. В приведенном выше примере компилятор может вставить ход из у1 к у3 в конце среднего левого блока и переход от у2 к у3 в конце среднего правого блока. Эти операции перемещения могут не попасть в окончательный код на основе компилятора распределение регистров процедура. Однако этот подход может не работать, когда одновременные операции спекулятивно производят входные данные для функции Φ, как это может случиться в широкий вопрос машины. Как правило, у широко распространенной машины есть инструкция выбора, используемая в таких ситуациях компилятором для реализации функции Φ.
По словам Кенни Задека,[5] Φ функции первоначально были известны как фальшивый функций, в то время как SSA разрабатывалась в IBM Research в 1980-х годах. Формальное название функции Φ было принято только тогда, когда работа была впервые опубликована в академической статье.
Вычисление минимального SSA с использованием границ доминирования
Во-первых, нам нужна концепция господин: мы говорим, что узел A строго доминирует другой узел B в графе потока управления, если невозможно достичь B, не пройдя сначала через A. Это полезно, потому что, если мы когда-нибудь дойдем до B, мы узнаем, что любой код в A запущен. Мы говорим, что A доминирует B (B есть доминировать над A) если либо A строго доминирует над B, либо A = B.
Теперь мы можем определить граница господства: узел B находится на границе доминирования узла A, если A не строго доминирует над B, но действительно доминирует над некоторым непосредственным предшественником B, или если узел A является непосредственным предшественником B, и, поскольку любой узел доминирует над самим собой, узел A доминирует над собой, и в результате узел A находится на границе доминирования узла B. С точки зрения A, это узлы, в которых другие пути управления, которые не проходят через A, появляются раньше всего.
Границы доминирования фиксируют точные места, в которых нам нужны функции Φ: если узел A определяет определенную переменную, то это определение и это определение в одиночку (или переопределения) достигнут каждого узла A доминирует. Только когда мы покидаем эти узлы и выходим на границу доминирования, мы должны учитывать другие потоки, вводя другие определения той же переменной. Более того, никакие другие функции Φ не нужны в графе потока управления, чтобы иметь дело с определениями A, и мы можем обойтись не меньшим.
Существует эффективный алгоритм определения границ доминирования каждого узла. Этот алгоритм изначально был описан в Cytron. и другие. 1991. Также полезна глава 19 книги Эндрю Аппеля "Современная реализация компилятора на Java" (Cambridge University Press, 2002). См. Статью для более подробной информации.[6]
Кейт Д. Купер, Тимоти Дж. Харви и Кен Кеннеди из Университет Райса описать алгоритм в своей статье под названием Простой и быстрый алгоритм доминирования.[7] Алгоритм использует хорошо спроектированные структуры данных для повышения производительности. Это выражается просто так:[7]
для каждого узел b dominance_frontier (b): = {}для каждого узел b если число непосредственных предшественников b ≥ 2 для каждого п в непосредственные предшественники b runner: = p в то время как бегун ≠ idom (b) dominance_frontier (бегун): = dominance_frontier (бегун) ∪ {b} runner: = idom (бегун)Примечание: в приведенном выше коде непосредственным предшественником узла n является любой узел, от которого управление передается узлу n, а idom (b) - это узел, который немедленно доминирует над узлом b (одноэлементный набор).
Вариации, уменьшающие количество Ф-функций
«Минимальный» SSA вставляет минимальное количество функций Φ, необходимых для обеспечения того, чтобы каждому имени было присвоено значение ровно один раз, и что каждая ссылка (использование) имени в исходной программе все еще может ссылаться на уникальное имя. (Последнее требование необходимо, чтобы компилятор мог записать имя для каждого операнда в каждой операции.)
Однако некоторые из этих функций Φ могут быть мертвых. По этой причине минимальный SSA не обязательно дает наименьшее количество Φ функций, необходимых для конкретной процедуры. Для некоторых типов анализа эти функции Φ излишни и могут привести к снижению эффективности анализа.
Обрезанный SSA
Урезанная форма SSA основана на простом наблюдении: функции Φ нужны только для переменных, которые «живы» после функции Φ. (Здесь «живое» означает, что значение используется на некотором пути, который начинается с рассматриваемой функции Φ.) Если переменная не является действующей, результат функции Φ не может быть использован, и присвоение функцией Φ не выполняется. .
Создание сокращенной формы SSA использует живая переменная информация на этапе вставки Φ-функции, чтобы решить, нужна ли данная Φ-функция. Если исходное имя переменной отсутствует в точке вставки функции Φ, функция Φ не вставляется.
Другой вариант - рассматривать обрезку как устранение мертвого кода проблема. Тогда функция Φ является активной только в том случае, если какое-либо использование во входной программе будет переписано в нее, или если она будет использоваться в качестве аргумента в другой функции Φ. При вводе формы SSA каждое использование переписывается до ближайшего определения, которое в нем доминирует. Тогда функция Φ будет считаться активной, если это ближайшее определение, которое доминирует по крайней мере одно использование или по крайней мере один аргумент действующего Φ.
Полуобрезанный SSA
Полуобрезанная форма SSA[8] - это попытка уменьшить количество функций Φ без относительно высоких затрат на вычисление информации о текущих переменных. Он основан на следующем наблюдении: если переменная никогда не становится активной после входа в базовый блок, ей никогда не нужна функция Φ. При построении SSA функции Φ для любых «блочно-локальных» переменных опускаются.
Вычисление набора локальных переменных блока является более простой и быстрой процедурой, чем полный анализ динамических переменных, что делает полу-сокращенную форму SSA более эффективной для вычислений, чем сокращенную форму SSA. С другой стороны, полуобрезанная форма SSA будет содержать больше функций Φ.
Преобразование формы SSA
Форма SSA обычно не используется для прямого выполнения (хотя ее можно интерпретировать[9]), и он часто используется «поверх» другого IR, с которым он остается в прямом соответствии. Это может быть достигнуто путем «построения» SSA как набора функций, которые сопоставляют части существующего IR (базовые блоки, инструкции, операнды, и т.п.) и его аналог SSA. Когда форма SSA больше не нужна, эти функции сопоставления могут быть отброшены, оставив только теперь оптимизированный IR.
Оптимизация формы SSA обычно приводит к запутанным SSA-Webs, что означает, что существуют инструкции Φ, не все операнды которых имеют одинаковый корневой операнд. В таких случаях окраска алгоритмы используются для выхода из SSA. Наивные алгоритмы вводят копию по каждому пути предшественника, что заставляет источник другого корневого символа быть помещенным в Φ, чем место назначения Φ. Существует несколько алгоритмов выхода из SSA с меньшим количеством копий, большинство из них используют графы интерференции или некоторое их приближение для объединения копий.[10]
Расширения
Расширения формы SSA можно разделить на две категории.
Схема переименования расширения изменяют критерий переименования. Напомним, что форма SSA переименовывает каждую переменную, когда ей присваивается значение. Альтернативные схемы включают статическую форму одноразового использования (которая переименовывает каждую переменную в каждом операторе при ее использовании) и статическую форму единой информации (которая переименовывает каждую переменную, когда ей присваивается значение, и на границе пост-доминирования).
Особенности расширения сохраняют единственное свойство присваивания для переменных, но включают новую семантику для моделирования дополнительных функций. Некоторые специализированные расширения моделируют такие функции языка программирования высокого уровня, как массивы, объекты и указатели с псевдонимами. Другие специфические для функций расширения моделируют низкоуровневые архитектурные особенности, такие как предположения и предсказания.
Компиляторы, использующие форму SSA
Эта секция может содержать неизбирательный, чрезмерный, или несущественный Примеры. (Август 2018 г.) |
Форма SSA - относительно недавняя разработка сообщества компиляторов. Таким образом, многие старые компиляторы используют форму SSA только для некоторой части процесса компиляции или оптимизации, но большинство из них не полагаются на нее. Примеры компиляторов, которые сильно зависят от формы SSA, включают:
- ETH Оберон-2 compiler был одним из первых общедоступных проектов, включающих "GSA", вариант SSA.
- В LLVM Инфраструктура компилятора использует форму SSA для всех значений скалярных регистров (всего, кроме памяти) в своем первичном представлении кода. Форма SSA удаляется только после того, как происходит выделение регистров, в конце процесса компиляции (часто во время компоновки).
- В Открыть64 компилятор использует форму SSA в своем глобальном скалярном оптимизаторе, хотя код передается в форму SSA и затем удаляется из формы SSA. Open64 использует расширения формы SSA для представления памяти в форме SSA, а также скалярных значений.
- Начиная с версии 4 (выпущенной в апреле 2005 г.) GCC, Коллекция компиляторов GNU, широко использует SSA. В фронты генерировать "GENERIC "код, который затем преобразуется в"GIMPLE "gimplifier". Затем к SSA-форме "GIMPLE" применяются высокоуровневые оптимизации. Полученный оптимизированный промежуточный код затем транслируется в RTL, к которому применяются низкоуровневые оптимизации. Специфическая для архитектуры бэкэнды наконец превратить RTL в язык ассемблера.
- IBM адаптивный Виртуальная машина Java, Jikes RVM, использует расширенный Array SSA, расширение SSA, которое позволяет анализировать скаляры, массивы и поля объектов в единой структуре. Анализ SSA с расширенным массивом доступен только на максимальном уровне оптимизации, который применяется к наиболее часто выполняемым частям кода.
- В 2002, исследователи модифицировали IBM JikesRVM (в то время называвшаяся Jalapeño) для запуска как стандартных Java байт-код и безопасный тип SSA (SafeTSA ) файлы классов байт-кода и продемонстрировали значительные преимущества в производительности при использовании байт-кода SSA.
- Oracle с Виртуальная машина Java HotSpot использует в своем JIT-компиляторе промежуточный язык на основе SSA.[11]
- Microsoft Visual C ++ серверная часть компилятора доступна в Microsoft Visual Studio Обновление 3 2015 года использует SSA [12]
- Мононуклеоз использует SSA в своем JIT-компиляторе Mini.
- jackcc это компилятор с открытым исходным кодом для набора академических инструкций Jackal 3.0. Он использует простой код с тремя операндами и SSA для его промежуточного представления. В качестве интересного варианта он заменяет функции Φ так называемой инструкцией SAME, которая инструктирует распределителю регистров поместить два активных диапазона в один и тот же физический регистр.
- Хотя это и не компилятор, Бумеранг декомпилятор использует SSA-форму во внутреннем представлении. SSA используется для упрощения распространения выражений, определения параметров и возвращаемых значений, анализа сохранения и многого другого.
- Portable.NET использует SSA в своем JIT-компиляторе.
- libFirm Полностью графическое промежуточное представление SSA для компиляторов. libFirm использует форму SSA для всех значений скалярных регистров до генерации кода с помощью распределителя регистров с поддержкой SSA.
- Концертный составитель штата Иллинойс, около 1994 г.[13] использовали вариант SSA под названием SSU (Static Single Use), который переименовывает каждую переменную, когда ей присваивается значение, и в каждом условном контексте, в котором эта переменная используется; по существу статическая единая информационная форма, упомянутая выше. Форма SSU оформлена в Кандидатская диссертация Джона Плевяка.
- Компилятор COINS использует оптимизацию формы SSA, как описано здесь: http://www.is.titech.ac.jp/~sassa/coins-www-ssa/english/
- В Mozilla Fire Fox ПаукОбезьяна Движок JavaScript использует IR на основе SSA.[14]
- В Хром Двигатель JavaScript V8 реализует SSA в своей инфраструктуре компилятора Crankshaft как объявлено в декабре 2010 г.
- PyPy использует линейное представление SSA для трассировок в своем JIT-компиляторе.
- Android с Дальвик виртуальная машина использует SSA в своем JIT-компиляторе.
- Android новый оптимизирующий компилятор для Android Runtime использует SSA для своего IR.
- Компилятор Standard ML MLton использует SSA на одном из промежуточных языков.
- LuaJIT активно использует оптимизацию на основе SSA.[15]
- В PHP и Взломать компилятор HHVM использует SSA в своих IR.[16]
- Компилятор R-Stream от Reservoir Labs поддерживает не-SSA (список квадрантов), SSA и SSI (статическая единичная информация[17]) формы.[18]
- Идти (1.7: только для архитектуры x86-64; 1.8: для всех поддерживаемых архитектур).[19][20]
- СПИР-В, стандарт языка затенения для Графический API Vulkan и язык ядра для OpenCL compute API, это представление SSA.[21]
- Различный Меса драйверы через NIR, представление SSA для языков затенения.[22]
- WebKit использует SSA в своих JIT-компиляторах.[23][24]
- Swift определяет свою собственную форму SSA над LLVM IR, называемую SIL (Swift Intermediate Language).[25][26]
- Erlang переписали свой компилятор в OTP 22.0, чтобы «внутренне использовать промежуточное представление, основанное на статическом одиночном назначении (SSA)». С планами по дальнейшей оптимизации, построенным на основе SSA в будущих выпусках.[27]
использованная литература
Заметки
- ^ Барри Розен; Марк Н. Вегман; Ф. Кеннет Задек (1988). «Числа глобальных значений и избыточные вычисления» (PDF). Материалы 15-го симпозиума ACM SIGPLAN-SIGACT по принципам языков программирования.
- ^ Ситрон, Рон; Ферранте, Жанна; Розен, Барри К .; Вегман, Марк Н. и Задек, Ф. Кеннет (1991). «Эффективное вычисление статической формы единственного назначения и графика зависимости управления» (PDF). Транзакции ACM по языкам и системам программирования. 13 (4): 451–490. CiteSeerX 10.1.1.100.6361. Дои:10.1145/115372.115320. S2CID 13243943.
- ^ Келси, Ричард А. (1995). «Соответствие между стилем передачи продолжения и статической формой одиночного присвоения» (PDF). Материалы семинара ACM SIGPLAN 1995 года по промежуточным представлениям: 13–22. Дои:10.1145/202529.202532. ISBN 0897917545. S2CID 6207179.
- ^ распространение диапазона значений
- ^ см. стр. 43 [«Происхождение Ф-функций и название»] Задека, Ф. Кеннета, Презентация по истории SSA на SSA'09 Семинар, Отран, Франция, апрель 2009 г.
- ^ Ситрон, Рон; Ферранте, Жанна; Розен, Барри К .; Wegman, Mark N .; Задек, Ф. Кеннет (1 октября 1991 г.). «Эффективное вычисление статической формы единого назначения и графика зависимости управления». Транзакции ACM по языкам и системам программирования. 13 (4): 451–490. Дои:10.1145/115372.115320. S2CID 13243943.
- ^ а б Купер, Кейт Д.; Харви, Тимоти Дж .; Кеннеди, Кен (2001). «Простой и быстрый алгоритм доминирования» (PDF). Цитировать журнал требует
| журнал =(Помогите) - ^ Бриггс, Престон; Купер, Кейт Д.; Харви, Тимоти Дж .; Симпсон, Л. Тейлор (1998). «Практические улучшения в построении и разрушении статической формы единого назначения» (PDF). Архивировано из оригинал (PDF) на 07.06.2010. Цитировать журнал требует
| журнал =(Помогите) - ^ фон Ронне, Джеффри; Нин Ван; Майкл Франц (2004). «Устный перевод программ в статической форме разового задания». Цитировать журнал требует
| журнал =(Помогите) - ^ Буассино, Бенуа; Дарте, Ален; Растелло, Фабрис; Динешин, Бенуа Дюпон де; Гийон, Кристоф (2008). «Пересмотр перевода вне SSA на предмет правильности, качества кода и эффективности». HAL-Inria Cs.DS: 14.
- ^ «Архитектура механизма производительности Java HotSpot». Корпорация Oracle.
- ^ «Представляем новый усовершенствованный оптимизатор кода Visual C ++».
- ^ "Концертный проект Иллинойса".
- ^ «Обзор IonMonkey».,
- ^ «Оптимизация байт-кода». проект LuaJIT.
- ^ "Представительство HipHop Intermediate (HHIR)".
- ^ Ананян, К. Скотт; Ринард, Мартин (1999). «Статическая единая информационная форма». CiteSeerX 10.1.1.1.9976. Цитировать журнал требует
| журнал =(Помогите) - ^ «Энциклопедия параллельных вычислений».
- ^ «Примечания к выпуску Go 1.7 - язык программирования Go». golang.org. Получено 2016-08-17.
- ^ «Примечания к выпуску Go 1.8 - язык программирования Go». golang.org. Получено 2017-02-17.
- ^ "СПИР-В спец" (PDF).
- ^ Экстранд, Джейсон. "Повторное внедрение NIR, нового IR для mesa".
- ^ «Знакомство с WebKit FTL JIT».
- ^ "Представляем JIT-компилятор B3".
- ^ "Swift Intermediate Language (GitHub)".
- ^ «Высокоуровневый IR Swift: пример дополнения LLVM IR с помощью языковой оптимизации, встреча разработчиков LLVM 10/2015».
- ^ «Примечания к выпуску OTP 22.0».
Общие ссылки
- Аппель, Эндрю В. (1999). Современная реализация компилятора в ML. Издательство Кембриджского университета. ISBN 978-0-521-58274-2. Также доступно в Ява (ISBN 0-521-82060-X, 2002) и C (ISBN 0-521-60765-5, 1998) версии.
- Купер, Кейт Д. и Торцон, Линда (2003). Разработка компилятора. Морган Кауфманн. ISBN 978-1-55860-698-2.
- Мучник, Стивен С. (1997). Расширенный дизайн и реализация компилятора. Морган Кауфманн. ISBN 978-1-55860-320-2.
- Келси, Ричард А. (март 1995 г.). «Соответствие между стилем прохождения продолжения и статической формой одиночного присвоения». Уведомления ACM SIGPLAN. 30 (3): 13–22. Дои:10.1145/202530.202532.
- Аппель, Эндрю В. (апрель 1998 г.). «SSA - это функциональное программирование». Уведомления ACM SIGPLAN. 33 (4): 17–20. Дои:10.1145/278283.278285. S2CID 207227209.
- Поп, Себастьян (2006). «Структура представления SSA: семантика, анализ и реализация GCC» (PDF). Цитировать журнал требует
| журнал =(Помогите) - Маттиас Браун; Себастьян Бухвальд; Себастьян Хак; Роланд Лейса; Кристоф Мэллон; Андреас Цвинкау (2013), «Простое и эффективное построение статической единой формы назначения», Конструкция компилятора, Конспект лекций по информатике, 7791, Springer Berlin Heidelberg, стр. 102–122, Дои:10.1007/978-3-642-37051-9_6, ISBN 978-3-642-37050-2, получено 24 марта 2013
внешние ссылки
- Босчер, Стивен; и Новильо, Диего. GCC получает новую платформу оптимизатора. Статья об использовании SSA в GCC и его улучшении по сравнению с более старыми IR.
- Библиография SSA. Обширный каталог исследовательских работ SSA.
- Задек, Ф. Кеннет. «Разработка статической единой формы назначения», Декабрь 2007 г., разговор о происхождении SSA.
- В.В.А.А. «Дизайн компилятора на основе SSA» (2014)

