Строковый график - String graph
В теория графов, а строковый граф является граф пересечений из кривые в плоскости; каждая кривая называется «струной». Учитывая график грамм, грамм является строковым графом тогда и только тогда, когда существует набор кривых или строк, нарисованных на плоскости, таких, что никакие три строки не пересекаются в одной точке, и такой, что граф имеет вершину для каждой кривой и ребро для каждой пересекающейся пары кривых изоморфна грамм.
Фон
Сеймур Бензер (1959 ) описал концепцию, аналогичную строковым графам, применительно к генетическим структурам. В этом контексте он также представил конкретный случай пересечения интервалов на прямой, а именно теперь классическое семейство интервальные графики. Потом, Синден (1966) указали ту же идею на электрические сети и печатные схемы. Математическое изучение строковых графов началось с статьи Эрлих, Эвен и Тарджан (1976) и благодаря сотрудничеству между Sinden и Рональд Грэм, где характеристика строковых графов в конечном итоге стала открытым вопросом на 5-м венгерском коллоквиуме по комбинаторике в 1976 году.[1] Однако в конечном итоге оказалось, что распознавание строковых графов НП-полный, подразумевая, что не существует простой характеристики.[2]
Связанные классы графов

Каждый планарный граф это строковый граф:[3] можно сформировать представление в виде строкового графа произвольного графа, вложенного в плоскость, путем рисования строки для каждой вершины, которая проходит вокруг вершины и вокруг средней точки каждого смежного ребра, как показано на рисунке. Для любого края УФ графа, строки для ты и v дважды пересекать друг друга около середины УФ, и других пересечений нет, поэтому пары пересекающихся строк представляют в точности смежные пары вершин исходного плоского графа. В качестве альтернативы теорема об упаковке кругов, любой плоский граф может быть представлен в виде набора окружностей, любые две из которых пересекаются тогда и только тогда, когда соответствующие вершины смежны; эти круги (с выбранной начальной и конечной точкой, чтобы превратить их в открытые кривые) представляют собой строковое графическое представление данного плоского графа. Чалопен, Гонсалвес и Очем (2007) Доказано, что каждый планарный граф имеет строковое представление, в котором каждая пара строк имеет не более одной точки пересечения, в отличие от представлений, описанных выше.Гипотеза Шайнермана Теперь доказано, что это еще более сильное утверждение, что любой планарный граф может быть представлен графом пересечений отрезков прямых, очень частным случаем строк.
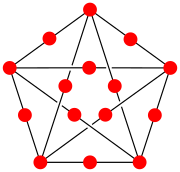
Если каждое ребро данного графа грамм является подразделяется, результирующий граф является строковым тогда и только тогда, когда грамм плоский. В частности, подразделение полный график K5 показанный на иллюстрации не является строковым графом, потому что K5 не плоский.[3]
Каждый круговой график, как граф пересечений отрезков прямой (хорды окружности), также является строковым графом. Каждый хордовый граф может быть представлен в виде строкового графа: хордовые графы - это графы пересечений поддеревьев деревьев, и можно сформировать строковое представление хордового графа, сформировав планарное вложение соответствующего дерева и заменив каждое поддерево строкой, которая проходит вокруг дерева поддерева. края.
В дополнительный граф каждого график сопоставимости также является строковым графом.[4]
Другие результаты
Эрлих, Эвен и Тарджан (1976) показал, что вычисление хроматического числа строковых графов является NP-трудным. Краточвиль (1991a) обнаружил, что строковые графы образуют индуцированный второстепенный замкнутый класс, но не второстепенный закрытый класс графов.
Каждый м-реберный строковый граф можно разделить на два подмножества, каждое из которых является постоянной долей размера всего графа, путем удаления О(м3/4бревно1/2м) вершины. Отсюда следует, что строковые графы без бикликов, строковые графы, не содержащие Kт,т подграф для некоторой константы т, имеют О(п) ребра и более сильно имеют полиномиальное разложение.[5]
Примечания
- ^ Грэм (1976).
- ^ Краточвиль (1991b) показал, что распознавание строкового графа является NP-трудным, но не смог показать, что это может быть решено в NP. После промежуточных результатов Шефер и Штефанкович (2001) и Пах и Тот (2002), Шефер, Седжвик и Штефанкович (2003) завершили доказательство NP-полноты задачи.
- ^ а б Шефер и Штефанкович (2001) доверять это наблюдение Синден (1966).
- ^ Голумбик, Ротем и Уррутия (1983) и Ловас (1983). Смотрите также Фокс и Пач (2010).
- ^ Фокс и Пач (2010); Дворжак и Норин (2015).
Рекомендации
- Бензер, С. (1959), «О топологии тонкой генетической структуры», Труды Национальной академии наук Соединенных Штатов Америки, 45 (11): 1607–1620, Bibcode:1959ПНАС ... 45.1607Б, Дои:10.1073 / pnas.45.11.1607, ЧВК 222769, PMID 16590553.
- Chalopin, J .; Gonçalves, D .; Очем, П. (2007), "Планарные графы в 1-STRING", Материалы восемнадцатого ежегодного симпозиума ACM-SIAM по дискретным алгоритмам, ACM и SIAM, стр. 609–617..
- Дворжак, Зденек; Норин, Сергей (2015), Сильно сублинейные разделители и полиномиальное разложение, arXiv:1504.04821, Bibcode:2015arXiv150404821D.
- Эрлих, G .; Даже, S .; Тарьян, Р.Э. (1976), «Графики пересечений кривых на плоскости», Журнал комбинаторной теории, 21 (1): 8–20, Дои:10.1016/0095-8956(76)90022-8.
- Фокс, Джейкоб; Пах, Янош (2010), «Теорема о разделителе для строковых графов и ее приложения», Комбинаторика, теория вероятностей и вычисления, 19 (3): 371, Дои:10.1017 / s0963548309990459.
- Golumbic, M .; Rotem, D .; Уррутия, Дж. (1983), «Графы сопоставимости и графы пересечений», Дискретная математика, 43 (1): 37–46, Дои:10.1016 / 0012-365X (83) 90019-5.
- Грэм, Р. Л. (1976), «Проблема 1», Открытые задачи на 5-м Венгерском коллоквиуме по комбинаторике.
- Краточвил Ян (1991a), "Строковые графы. I. Число критических нестроковых графов бесконечно", Журнал комбинаторной теории, серия B, 52 (1): 53–66, Дои:10.1016/0095-8956(91)90090-7.
- Краточвил Ян (1991b), "Строковые графы. II. Распознавание строковых графов NP-сложно", Журнал комбинаторной теории, серия B, 52 (1): 67–78, Дои:10.1016 / 0095-8956 (91) 90091-В.
- Ловас, Л. (1983), «Совершенные графы», Избранные темы теории графов, 2, Лондон: Academic Press, стр. 55–87..
- Пах, Янош; Тот, Геза (2002), "Распознавание строковых графов разрешимо", Дискретная и вычислительная геометрия, 28 (4): 593–606, Дои:10.1007 / s00454-002-2891-4.
- Шефер, Маркус; Штефанкович, Даниэль (2001), «Разрешимость строковых графов», Материалы 33-го ежегодного симпозиума ACM по теории вычислений (STOC 2001): 241–246.
- Шефер, Маркус; Седжвик, Эрик; Штефанкович, Даниэль (2003), «Распознавание строковых графов в NP», Журнал компьютерных и системных наук, 67 (2): 365–380, Дои:10.1016 / S0022-0000 (03) 00045-X.
- Sinden, F. W. (1966), "Топология тонкопленочных RC-цепей", Технический журнал Bell System, 45 (9): 1639–1662, Дои:10.1002 / j.1538-7305.1966.tb01713.x.
