Примеры машины Тьюринга - Turing machine examples

Ниже приведены примеры, дополняющие статью. Машина Тьюринга.

Самый первый пример Тьюринга

Следующая таблица - самый первый пример Тьюринга (Алан Тьюринг 1937):

«1. Можно сконструировать машину для вычисления последовательности 0 1 0 1 0 1 ...» (0 <пусто> 1 <пусто> 0 ...) (Неразрешимый п. 119)

Конфигурация		Поведение
м-конфигурация (государственный)	Лента символ	Ленточные операции	Окончательная м-конфигурация (государственный)
б	пустой	P0, R	c
c	пустой	р	е
е	пустой	P1, R	ж
ж	пустой	р	б

Что касается действий машины на самом деле, Тьюринг (1936) (Неразрешимый п. 121) утверждает следующее:

"Эта [примерная] таблица (и все последующие таблицы того же типа) должны пониматься как означающие, что для конфигурации, описанной в первых двух столбцах, операции в третьем столбце выполняются последовательно, а затем машина переходит в m-конфигурация в последнем столбце ". (Неразрешимо, стр.121)

Он делает это очень ясно, когда сокращает приведенную выше таблицу до одной инструкции под названием «b» (Неразрешимый п. 120), но его инструкция состоит из 3 строк. Инструкция «b» имеет три различных варианта символа {Нет, 0, 1}. За каждой возможностью следует последовательность действий, пока мы не дойдем до крайнего правого столбца, где окончательная m-конфигурация - «b»:

Текущая м-конфигурация (инструкция)	Лента символ	Операции на ленте	Окончательная м-конфигурация (инструкция)
б	Никто	P0	б
б	0	R, R, P1	б
б	1	R, R, P0	б

По наблюдениям ряда комментаторов, включая самого Тьюринга (1937) (например, Пост (1936), Пост (1947), Клини (1952), Ван (1954)), инструкции Тьюринга не атомарны - дальнейшие упрощения модели могут производиться без снижения его вычислительной мощности; увидеть больше на Машина Пост-Тьюринга.

Как сказано в статье Машина Тьюринга Тьюринг предложил еще больше атомизировать его таблицу, разрешив только одну печать / стирание с последующим одним движением ленты L / R / N. Он дает нам этот пример преобразования первого маленького стола (Неразрешимый, п. 127):

Текущая m-конфигурация (состояние Тьюринга)	Лента символ	Печать-операция	Лента-движение	Окончательная m-конфигурация (состояние Тьюринга)
q1	пустой	P0	р	q2
q2	пустой	P пусто, т.е. E	р	q3
q3	пустой	P1	р	q4
q4	пустой	P пусто, т.е. E	р	q1

Утверждение Тьюринга по-прежнему подразумевает пять атомарных операций. По заданной инструкции (m-конфигурация) машина:

1. наблюдает за лентой-символом под головой
2. на основе наблюдаемого символа переходит к соответствующей последовательности инструкций для использования
3. печатает символ S_j или стирает, или ничего не делает
4. перемещает ленту влево, вправо или вообще не перемещает
5. переходит к последней m-конфигурации для этого символа

Поскольку действия машины Тьюринга не являются атомарными, моделирование машины должно разбивать каждую кортеж из пяти на последовательность более простых действий. Одна из возможностей - использованная в следующих примерах «поведения» его машины - следующая:

(q_я) Тестовая лента-символ под заголовком: если символ S₀ перейти к q_я.01, если символ S₁ перейти к q_я.11, если символ S₂ перейти к q_я.21 и др.

(q_я.01) выведите символ S_j0 или стереть или ничего не делать, затем перейти к q_я.02

(q_я.02) переместите ленту влево или вправо, а затем перейдите к qm0

(q_я.11) выведите символ S_j1 или стереть или ничего не делать, затем перейти к q_я.12

(q_я.12) переместите ленту влево или вправо, а затем перейдите к qm1

(q_я.21) выведите символ S_j2 или стереть или ничего не делать, затем перейти к q_я.22

(q_я.22) переместите ленту влево или вправо, а затем перейдите к qm2

(и т. д. - все символы должны быть учтены)

Так называемые «канонические» конечные автоматы провести символьные тесты «параллельно»; увидеть больше на микропрограммирование.

В следующем примере того, что делает машина, мы отметим некоторые особенности моделей Тьюринга:

«Условие написания цифр только на чередующихся квадратах очень полезно: я всегда буду им пользоваться». (Неразрешимо, стр.121)

Таким образом, при печати он пропускает все остальные квадраты. Напечатанные квадраты называются F-квадратами; пустые квадраты между ними могут использоваться в качестве «маркеров» и называются «E-квадратами», как в слове «подлежащие стиранию». F-квадраты, в свою очередь, являются его «квадратами фигуры» и содержат только символы 1 или 0 - символы, которые он назвал «цифрами» (как в «двоичных числах»).

В этом примере лента начинается с «пустой», а затем на ней печатаются «цифры». Для краткости здесь показаны только ТАБЛИЧНЫЕ состояния:

Последовательность	Идентификатор инструкции					Голова
		.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.
1	1	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.
2	2	.	.	.	.	.	0	.	.	.	.	.	.	.	.	.	.	.	.
3	3	.	.	.	.	.	.	0	.	.	.	.	.	.	.	.	.	.	.
4	4	.	.	.	.	.	1	.	0	.	.	.	.	.	.	.	.	.	.
5	1	.	.	.	.	.	.	1	.	0	.	.	.	.	.	.	.	.	.
6	2	.	.	.	.	.	0	.	1	.	0	.	.	.	.	.	.	.	.
7	3	.	.	.	.	.	.	0	.	1	.	0	.	.	.	.	.	.	.
8	4	.	.	.	.	.	1	.	0	.	1	.	0	.	.	.	.	.	.
9	1	.	.	.	.	.	.	1	.	0	.	1	.	0	.	.	.	.	.
10	2	.	.	.	.	.	0	.	1	.	0	.	1	.	0	.	.	.	.
11	3	.	.	.	.	.	.	0	.	1	.	0	.	1	.	0	.	.	.
12	4	.	.	.	.	.	1	.	0	.	1	.	0	.	1	.	0	.	.
13	1	.	.	.	.	.	.	1	.	0	.	1	.	0	.	1	.	0	.
14	2	.	.	.	.	.	0	.	1	.	0	.	1	.	0	.	1	.	0

Тот же «прогон» со всеми промежуточными лентами и движениями показан здесь:

При внимательном рассмотрении таблицы обнаруживаются определенные проблемы с собственным примером Тьюринга - не все символы учтены.

Например, предположим, что его лента изначально не была пустой. Что случилось бы? Машина Тьюринга считывала значения, отличные от предполагаемых.

Подпрограмма копирования

Это очень важная подпрограмма, используемая в подпрограмме "умножение".

Пример машины Тьюринга обрабатывает строку из нулей и единиц, где 0 представлен пустым символом. Его задача - удвоить любую встреченную на ленте серию единиц, записав между ними 0. Например, когда головка читает «111», она записывает 0, а затем «111». На выходе будет «1110111».

Для выполнения своей задачи этой машине Тьюринга потребуется всего 5 состояний работы, которые называются {s₁, с₂, с₃, с₄, с₅}. Каждое состояние выполняет 4 действия:

1. Прочтите символ под головой
3. Запишите выходной символ, определяемый состоянием
5. Переместите ленту влево или вправо в зависимости от штата.
7. Переключитесь в следующее состояние, определяемое текущим состоянием

Начальная m-конфигурация (текущая инструкция)	Лента символ	Операция печати	Движение ленты	Окончательная m-конфигурация (следующая инструкция)
s1	0	N	N	ЧАС
s1	1	E	р	s2
s2	0	E	р	s3
s2	1	P1	р	s2
s3	0	P1	L	s4
s3	1	P1	р	s3
s4	0	E	L	s5
s4	1	P1	L	s4
s5	0	P1	р	s1
s5	1	P1	L	s5
ЧАС	-	-	-

«Прогон» машинных последовательностей через 16 машинных конфигураций (также известных как состояния Тьюринга):

Последовательность	Идентификатор инструкции						Голова
1	s1	0	0	0	0	1	1	0	0	0	0	0
2	s2	0	0	0	0	0	1	0	0	0	0	0
3	s2	0	0	0	0	0	0	1	0	0	0	0
4	s3	0	0	0	0	0	0	0	1	0	0	0
5	s4	0	0	0	0	1	0	1	0	0	0	0
6	s5	0	0	0	1	0	1	0	0	0	0	0
7	s5	0	0	1	0	1	0	0	0	0	0	0
8	s1	0	0	0	1	0	1	1	0	0	0	0
9	s2	0	0	0	0	1	0	0	1	0	0	0
10	s3	0	0	0	0	0	1	0	0	1	0	0
11	s3	0	0	0	0	0	0	1	0	0	1	0
12	s4	0	0	0	0	1	1	0	0	1	0	0
13	s4	0	0	0	1	1	0	0	1	0	0	0
14	s5	0	0	1	1	0	0	1	0	0	0	0
15	s1	0	0	0	1	1	0	1	1	0	0	0
16	ЧАС	0	0	0	1	1	0	1	1	0	0	0

Поведение этой машины можно описать как цикл: он начинается через s₁, заменяет первую 1 на 0, затем использует s₂ переместиться вправо, пропуская 1 с и первый встреченный 0. s₃ затем пропускает следующую последовательность единиц (изначально их нет) и заменяет первый найденный 0 на 1. s₄ перемещается назад влево, пропуская 1 с, пока не найдет 0 и не переключится на s₅. s₅ затем перемещается влево, пропуская 1 с, пока не найдет 0, который изначально был записан s₁.

Он заменяет 0 на 1, перемещает на одну позицию вправо и вводит s₁ снова для еще одного круга петли.

Это продолжается до s₁ находит 0 (это 0 в середине двух строк из единиц), когда машина останавливается.

Альтернативное описание

В другом описании проблема заключается в том, как отслеживать количество единиц. Мы не можем использовать одно состояние для каждого возможного числа (состояние для каждого из 0,1,2,3,4,5,6 и т. Д.), Потому что тогда нам понадобятся бесконечные состояния для представления всех натуральных чисел, а конечный автомат конечный - нам придется как-то отследить это с помощью ленты.

Основной способ его работы - копирование каждой «1» на другую сторону, перемещение вперед и назад - он достаточно умен, чтобы запомнить, на какой части пути он находится. Более подробно, он переносит каждую «1» на другую сторону, распознавая разделяющий «0» в середине и распознавая «0» на другой стороне, чтобы знать, что он достиг конца. Он возвращается с использованием того же метода, обнаруживая средний «0», а затем «0» на исходной стороне. Этот «0» на исходной стороне - ключ к разгадке того, как он отслеживает количество единиц.

Хитрость в том, что перед переносом «1» он помечает эту цифру как «взятая», заменяя ее на «0». Когда он возвращается, он заполняет этот «0» обратно на «1», затем переходит к следующему, отметив его «0» и повторив цикл, перенося эту «1» и так далее. При каждом движении вперед и назад маркер «0» перемещается на один шаг ближе к центру.. Вот как он отслеживает, сколько «1» он принял.

Когда он возвращается, маркер «0» выглядит как конец набора «1» для него - любые «1», которые уже были пройдены, невидимы для него (на другой стороне маркера «0» ), и поэтому он как будто работает над (N-1) числом "1" s - аналогично доказательству математическая индукция.

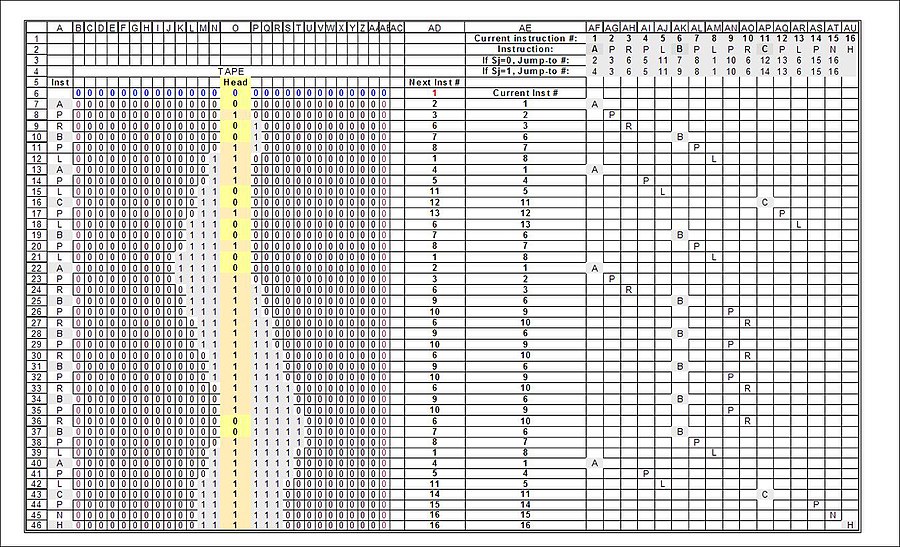
Полный «пробег» с отображением результатов промежуточных «движений». Чтобы лучше его увидеть, нажмите на изображение, а затем нажмите на загрузку с более высоким разрешением:

3 состояния Занятый Бобер

Следующая таблица инструкций Тьюринга была взята из Peterson (1988), стр. 198, рис. 7.15. Петерсон двигает головой; в следующей модели движется лента.

Лента символ	Текущее состояние А			Текущее состояние B			Текущее состояние C
	Написать символ	Переместить ленту	Следующее состояние	Написать символ	Переместить ленту	Следующее состояние	Написать символ	Переместить ленту	Следующее состояние
0	1	р	B	1	L	А	1	L	B
1	1	L	C	1	р	B	1	N	HALT

Рисунок «состояния» занятого бобра с 3 состояниями показывает внутренние последовательности событий, необходимые для фактического выполнения «состояния». Как отмечалось выше, Тьюринг (1937) совершенно ясно дает понять, что это правильная интерпретация кортежей из пяти, описывающих инструкцию (Неразрешимый, п. 119). Подробнее об атомизации 5-кортежей Тьюринга см. Машина Пост-Тьюринга:

В следующей таблице показан «сжатый» прогон - только состояния Тьюринга:

Последовательность	Идентификатор инструкции							Голова
1	б	0	0	0	0	0	0	0	0	0	0	0	0	0	0
2	B	0	0	0	0	0	0	0	1	0	0	0	0	0	0
3	А	0	0	0	0	0	1	1	0	0	0	0	0	0	0
4	C	0	0	0	0	1	1	0	0	0	0	0	0	0	0
5	B	0	0	0	1	1	1	0	0	0	0	0	0	0	0
6	А	0	0	1	1	1	1	0	0	0	0	0	0	0	0
7	B	0	0	0	1	1	1	1	1	0	0	0	0	0	0
8	B	0	0	0	0	1	1	1	1	1	0	0	0	0	0
9	B	0	0	0	0	0	1	1	1	1	1	0	0	0	0
10	B	0	0	0	0	0	0	1	1	1	1	1	0	0	0
11	B	0	0	0	0	0	0	0	1	1	1	1	1	0	0
12	А	0	0	0	0	0	1	1	1	1	1	1	0	0	0
13	C	0	0	0	0	1	1	1	1	1	1	0	0	0	0
14	ЧАС	0	0	0	0	1	1	1	1	1	1	0	0	0	0

Полный "пробег" занятого бобра с 3 состояниями. Полученные в результате состояния Тьюринга (то, что Тьюринг назвал «m-конфигурациями» - «конфигурациями машины») выделены серым цветом в столбце A, а также под инструкциями машины (столбцы AF-AU)):

Рекомендации

Для полных ссылок см. Машина Тьюринга.

• Иварс Петерсон, 1988 г., Математический турист: краткое изложение современной математики, W.H. Freeman and Company, Нью-Йорк, ISBN  0-7167-2064-7 (пбк.). Машины Тьюринга описаны на стр. 194 и далее, пример занятого бобра - на рис. 7.15 на стр. 198.
• Мартин Дэвис редактор, 1965, Неразрешимое: основные статьи о неразрешимых предложениях, неразрешимых задачах и вычислимых функциях, Raven Press, New York, без ISBN, без номера карты в каталоге.

• Алан Тьюринг, 1937 год, О вычислимых числах в приложении к Entscheidungsproblem, pp. 116ff, с кратким комментарием Дэвиса на странице 115.
• Алан Тьюринг, 1937 год, О вычислимых числах в приложении к Entscheidungsproblem. Исправление, п. 152-154.