Многоугольник видимости - Visibility polygon

Многоугольник видимости показан желтым. Четыре препятствия показаны синим цветом.

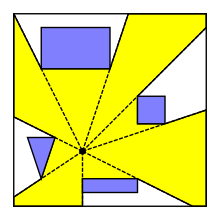
В вычислительная геометрия, то многоугольник видимости или же область видимости на точку п в плоскости среди препятствий возможно неограниченное полигональная область всех точек плоскости видимый из п. Многоугольник видимости можно также определить для видимости из сегмента или многоугольника. Полигоны видимости полезны в робототехника, видеоигры, и в определении позиций найти объекты, Такие как лучшее размещение охранников в картинной галерее.

Если многоугольник видимости ограничен, то это звездообразный многоугольник. Полигон видимости считается ограниченным, если все лучи, стреляющие из точки, в конечном итоге заканчиваются каким-либо препятствием. Это так, например, если препятствиями являются края простой многоугольник и п находится внутри многоугольника. В последнем случае многоугольник видимости может быть найден за линейное время.^[1][2][3][4]

Определения

Формально мы можем определить задачу плоского многоугольника видимости как таковую. Позволять ${displaystyle S}$ набор препятствий (отрезков или многоугольников) в ${displaystyle mathbb {R} ^{2}}$. Позволять ${displaystyle p}$ быть точкой в ${displaystyle mathbb {R} ^{2}}$ это не препятствие. Затем многоугольник видимости точки ${displaystyle V}$ это множество точек в ${displaystyle mathbb {R} ^{2}}$, так что для каждой точки ${displaystyle q}$ в ${displaystyle V}$, сегмент ${displaystyle pq}$ не пересекает никаких препятствий в ${displaystyle S}$.

Точно так же многоугольник видимости сегмента или же полигон видимости края видна ли часть из любой точки вдоль отрезок.

Приложения

Полигоны видимости полезны в робототехника. Например, в локализация роботов, робот, использующий датчики, такие как лидар будет обнаруживать препятствия, которые он может видеть, что похоже на многоугольник видимости.^[5]

Они также полезны в видеоигры, с многочисленными онлайн-руководствами, объясняющими простые алгоритмы его реализации.^[6][7][8]

Алгоритмы точечных полигонов видимости

Было предложено множество алгоритмов вычисления многоугольника видимости точки. Для разных вариантов задачи (например, для разных типов препятствий) алгоритмы различаются по временной сложности.

Наивные алгоритмы

Наивные алгоритмы легко понять и реализовать, но это не так. оптимальный, так как они могут быть намного медленнее других алгоритмов.

Единый "физический" алгоритм лучей

В реальной жизни светящаяся точка освещает видимую для нее область, потому что излучает свет во всех направлениях. Это можно смоделировать, стреляя лучи по многим направлениям. Предположим, что точка ${displaystyle p}$ и множество препятствий ${displaystyle S}$. Затем псевдокод может быть выражено следующим образом:

алгоритм naive_bad_algorithm (${displaystyle p}$, ${displaystyle S}$) является    ${displaystyle V}$ := ${displaystyle emptyset }$    за ${displaystyle heta =0,cdots ,2pi }$: // снимаем луч под углом ${displaystyle heta }$        ${displaystyle r}$ := ${displaystyle infty }$        для каждого препятствие в ${displaystyle S}$:            ${displaystyle r}$ : = мин (${displaystyle r}$, расстояние от ${displaystyle p}$ к препятствию в этом направлении) добавить вершину ${displaystyle ( heta ,r)}$ к ${displaystyle V}$    возвращаться ${displaystyle V}$

Если бы можно было попробовать все бесконечное множество углов, результат был бы правильным. К сожалению, невозможно по-настоящему попробовать каждое направление из-за ограничений компьютеров. Приближение может быть получено путем отражения множества, скажем, 50 равномерно разнесенных лучей. Однако это не точное решение, поскольку два соседних луча могут полностью пропустить небольшие препятствия. Кроме того, это очень медленно, поскольку для получения примерно аналогичного решения может потребоваться выстрелить большим количеством лучей, а выходной многоугольник видимости может иметь намного больше вершин, чем необходимо.

Приведение лучей к каждой вершине

Вышеописанный алгоритм можно значительно улучшить как по скорости, так и по точности, сделав наблюдение, что достаточно стрелять лучами только в каждую вершину препятствия. Это связано с тем, что любые изгибы или углы вдоль границы многоугольника видимости должны происходить из-за некоторого угла (то есть вершины) в препятствии.

алгоритм naive_better_algorithm (${displaystyle p}$, ${displaystyle S}$) является    ${displaystyle V}$ := ${displaystyle emptyset }$    для каждого препятствие ${displaystyle b}$ в ${displaystyle S}$:        для каждого вершина ${displaystyle v}$ из ${displaystyle b}$: // стреляем лучом из ${displaystyle p}$ к ${displaystyle v}$            ${displaystyle r}$ : = расстояние от ${displaystyle p}$ к ${displaystyle v}$            ${displaystyle heta }$ : = угол ${displaystyle v}$ относительно ${displaystyle p}$            для каждого препятствие ${displaystyle b'}$ в ${displaystyle S}$:                ${displaystyle r}$ : = мин (${displaystyle r}$, расстояние от ${displaystyle p}$ к ${displaystyle b'}$) добавить вершину ${displaystyle ( heta ,r)}$ к ${displaystyle V}$    возвращаться ${displaystyle V}$

Приведенный выше алгоритм может быть неверным. См. Обсуждение в разделе «Обсуждение».

Временная сложность этого алгоритма составляет ${displaystyle O(n^{2})}$. Это потому, что алгоритм направляет луч в каждую из ${displaystyle n}$ вершин, и чтобы проверить, где заканчивается луч, он должен проверить пересечение с каждым из ${displaystyle O(n)}$ препятствия. Этого достаточно для многих простых приложений, таких как видеоигры, и поэтому многие онлайн-руководства обучают этому методу.^[8] Однако, как мы увидим позже, есть более быстрые ${displaystyle O(nlog n)}$ алгоритмы (или даже более быстрые, если препятствие представляет собой простой многоугольник или есть фиксированное количество многоугольных отверстий).

Оптимальные алгоритмы для точки в простом многоугольнике

Многоугольник видимости для точки в центре (показан белым) внутри простого многоугольника, обведенного черным контуром.

Учитывая простой многоугольник ${displaystyle {mathcal {P}}}$ и точка ${displaystyle p}$, а линейное время алгоритм оптимален для расчета области в ${displaystyle {mathcal {P}}}$ что видно из ${displaystyle p}$. Такой алгоритм был впервые предложен в 1981 году.^[2] Однако это довольно сложно. В 1983 году был предложен концептуально более простой алгоритм,^[3] в котором была небольшая ошибка, исправленная в 1987 году.^[4]

Последний алгоритм будет кратко объяснен здесь. Он просто ходит по границе многоугольника ${displaystyle {mathcal {P}}}$, обрабатывая вершины в том порядке, в котором они появляются, сохраняя куча вершин ${displaystyle {mathcal {S}}=s_{0},s_{1},cdots ,s_{t}}$ куда ${displaystyle s_{t}}$ это вершина стека. Стек представляет собой встреченные до сих пор вершины, видимые для ${displaystyle p}$. Если позже во время выполнения алгоритма обнаруживаются новые вершины, которые закрывают часть ${displaystyle {mathcal {S}}}$, то закрытые вершины в ${displaystyle {mathcal {S}}}$ будет извлечен из стека. К моменту завершения работы алгоритма ${displaystyle {mathcal {S}}}$ будет состоять из всех видимых вершин, то есть желаемого многоугольника видимости. Эффективная реализация была опубликована в 2014 году.^[9]

Оптимальные алгоритмы для точки в многоугольнике с отверстиями

Для точки в многоугольнике с ${displaystyle h}$ дыры и ${displaystyle n}$ вершин, можно показать, что в худшем случае ${displaystyle Theta (n+hlog h)}$ алгоритм оптимален. Такой алгоритм был предложен в 1995 году вместе с доказательством его оптимальности.^[10] Однако он полагается на линейное время триангуляция многоугольника алгоритм Chazelle, который чрезвычайно сложен.

Оптимальные алгоритмы для точки среди сегментов

Сегменты, которые не пересекаются, кроме их конечных точек

Многоугольник видимости для точки в центре (показан белым) среди набора произвольных линейных сегментов на плоскости, которым разрешено пересекаться только в их конечных точках, действующих как препятствия (показаны черным).

Для точки среди набора ${displaystyle n}$ сегментов, которые не пересекаются, за исключением их конечных точек, можно показать, что в худшем случае ${displaystyle Theta (nlog n)}$ алгоритм оптимален. Это связано с тем, что алгоритм многоугольника видимости должен выводить вершины многоугольника видимости в отсортированном порядке, отсюда и проблема сортировка можно свести к вычислению многоугольника видимости.^[11]

Обратите внимание, что любой алгоритм, который вычисляет многоугольник видимости для точки среди сегментов, можно использовать для вычисления многоугольника видимости для всех других типов многоугольных препятствий, поскольку любой многоугольник можно разложить на сегменты.

Разделяй и властвуй

А алгоритм разделяй и властвуй для вычисления многоугольника видимости было предложено в 1987 году.^[12]

Угловая развертка

An угловая стреловидность, т.е. вращательный развертка алгоритм для вычисления многоугольника видимости был предложен в 1985 г.^[13] и 1986.^[11] Идея состоит в том, чтобы сначала отсортировать все конечные точки сегмента по полярному углу, а затем перебрать их в этом порядке. Во время итерации строка событий поддерживается как куча. Эффективная реализация была опубликована в 2014 году.^[9]

Обычно пересекающиеся сегменты

Для точки среди обычно пересекающихся сегментов проблема многоугольника видимости сводится за линейное время к нижний конверт проблема. Посредством Аргумент Давенпорта-Шинцеля, нижняя огибающая в худшем случае имеет ${displaystyle Theta (nalpha (n))}$ количество вершин, где ${displaystyle alpha (n)}$ это обратная функция Аккермана. Оптимальный алгоритм «разделяй и властвуй» наихудший случай, работающий в ${displaystyle Theta (nlog n)}$ время было создано Джон Хершбергер в 1989 г.^[14]

Рекомендации

1. Франко П. Препарата и Майкл Ян Шамос (1985). Вычислительная геометрия - Введение. Springer-Verlag. 1-е издание: ISBN  0-387-96131-3; 2-е издание, исправленное и расширенное, 1988 г .: ISBN  3-540-96131-3; Русский перевод, 1989 г .: ISBN  5-03-001041-6.
2. Эль-Гинди, Хоссам; Авис, Дэвид (1981). «Линейный алгоритм вычисления многоугольника видимости из точки». Журнал алгоритмов. 2 (2): 186–197. Дои:10.1016/0196-6774(81)90019-5.
3. Ли, Д. Т. (май 1983 г.). «Видимость простого многоугольника». Компьютерное зрение, графика и обработка изображений. 22 (2): 207–221. Дои:10.1016 / 0734-189X (83) 90065-8.
4. Джо, Барри; Симпсон, Р. Б. (1987). «Исправления к алгоритму многоугольника видимости Ли». BIT вычислительная математика. 27 (4): 458–473. Дои:10.1007 / BF01937271.
5. Гибас, Леонид; Мотвани, Раджив; Рагхаван, Прабхакар (1992). Проблема локализации робота в двух измерениях. Симпозиум ACM-SIAM по дискретным алгоритмам. Общество промышленной и прикладной математики.
6. Ляу, Никлаус. «SIGHT & LIGHT, как создать 2D-эффекты видимости / тени для вашей игры». Получено 9 мая 2014.
7. Патель, Амит (5 июля 2012 г.). «Алгоритм 2d видимости». Получено 9 мая 2014.
8. Патель, Амит (5 июля 2012 г.). «Кляксы в играх: двумерная видимость». Получено 9 мая 2014.
9. Бунджу, Франциск; Хеммер, Майкл; Хершбергер, Джон; Хуанг, Кан; Креллер, Александр (2014). «Эффективное вычисление многоугольников видимости». arXiv:1403.3905 [cs.CG ].
10. Хеффернан, Пол; Митчелл, Джозеф (1995). «Оптимальный алгоритм расчета видимости в самолете» (PDF). SIAM Журнал по вычислениям. 24 (1): 184–201. Дои:10.1137 / S0097539791221505.
11. Сури, Субхаш; О'Рурк, Джозеф (1986). Оптимальные алгоритмы наихудшего случая построения многоугольников видимости с дырами. Симпозиум по вычислительной геометрии. ACM. С. 14–23. Дои:10.1145/10515.10517.
12. Аркин, Э.; Митчелл, Джозеф (1987). Оптимальный алгоритм видимости для простого многоугольника с отверстиями в форме звезды (Технический отчет). Корнельский университет, исследования операций и промышленное строительство. 746.
13. Асано, Тецуо (1985). Эффективный алгоритм поиска многоугольника видимости многоугольной области с дырами. Институт инженеров электроники, информации и связи. 68. С. 557–559.
14. Хершбергер, Джон (1989). "Нахождение верхнего конверта ${displaystyle n}$ сегменты в ${displaystyle O(nlog n)}$ время". Письма об обработке информации. 33 (4): 169–174. Дои:10.1016/0020-0190(89)90136-1.

внешняя ссылка

• http://web.informatik.uni-bonn.de/I/GeomLab/VisPolygon/index.html.en (видимость простыми полигонами - апплетами)

Программного обеспечения

• VisiLibity: Бесплатная библиотека C ++ с открытым исходным кодом для вычислений видимости в плоских полигональных средах.
• видимость-многоугольник-js: Общедоступная библиотека Javascript для вычисления многоугольника видимости для точки среди сегментов с использованием метода угловой развертки.