Наклонный поворот - Banked turn - Wikipedia

А наклонный поворот (или же банковская очередь) - поворот или изменение направления, в котором транспортное средство кренится или наклоняется, обычно в сторону внутренней части поворота. Для автомобильных или железных дорог это обычно происходит из-за того, что полотно дороги имеет поперечный уклон вниз по направлению к внутренней части кривой. Угол крена - это угол, под которым автомобиль склонный относительно его продольной оси относительно горизонтали.

Включите плоские поверхности

Если угол крена равен нулю, поверхность плоская и нормальная сила вертикально вверх. Единственная сила, удерживающая автомобиль на своем пути, - это трение, или же тяга. Он должен быть достаточно большим, чтобы обеспечить центростремительная сила, соотношение, которое может быть выражено как неравенство, предполагая, что автомобиль движется по кругу радиусом р:

${\displaystyle \mu mg>{mv^{2} \over r}.}$

Выражение в правой части - это центростремительное ускорение, умноженное на массу, силу, необходимую для поворота транспортного средства. Левая часть - максимальная сила трения, которая равна коэффициент трения μ умноженное на нормальную силу. Изменение максимальной скорости поворота

${\displaystyle v<{\sqrt {r\mu g}}.}$

Обратите внимание, что μ может быть коэффициентом статического или динамического трения. В последнем случае, когда автомобиль скользит на повороте, трение достигает предела, и неравенства превращаются в уравнения. Это также игнорирует такие эффекты, как прижимная сила что может увеличить нормальную силу и скорость поворота.

Поворот без трения

Верхняя панель: мяч на круговой дорожке с наклоном, движущийся с постоянной скоростью v; Нижняя панель: Силы на шаре. Результирующее или равнодействующая сила на шаре, найденном векторное сложение из нормальная сила оказываемое дорогой и вертикальной силой из-за сила тяжести должна равняться силе, необходимой для центростремительного ускорения, продиктованной необходимостью движения по круговой траектории.

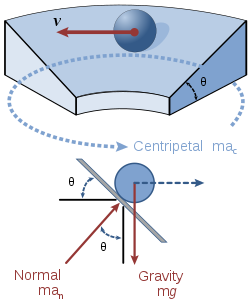
В отличие от транспортного средства, движущегося по плоскому кругу, наклонные края добавляют дополнительную силу, которая удерживает транспортное средство на его пути и предотвращает «втягивание» или «выталкивание» автомобиля за пределы круга (или движение железнодорожного колеса вбок. чтобы чуть не потереть колесо фланец ). Эта сила является горизонтальной составляющей нормальной силы транспортного средства. В отсутствие трения нормальная сила является единственной, действующей на транспортное средство в направлении центра круга. Следовательно, согласно второму закону Ньютона, мы можем установить горизонтальную составляющую нормальной силы равной массе, умноженной на центростремительное ускорение:^[1]

${\displaystyle N\sin \theta ={mv^{2} \over r}}$

Поскольку движение в вертикальном направлении отсутствует, сумма всех вертикальных сил, действующих на систему, должна быть равна нулю. Следовательно, мы можем установить вертикальную составляющую нормальной силы транспортного средства равной его массе:^[1]

${\displaystyle N\cos \theta =mg}$

Решая приведенное выше уравнение для нормальной силы и подставляя это значение в предыдущее уравнение, мы получаем:

${\displaystyle {mv^{2} \over r}={mg\tan \theta }}$

Это эквивалентно:

${\displaystyle {v^{2} \over r}={g\tan \theta }}$

Решая для скорости, мы имеем:

${\displaystyle v={\sqrt {rg\tan \theta }}}$

Это обеспечивает скорость, которая при отсутствии трения и заданном угле наклона и радиус кривизны, гарантирует, что автомобиль останется на заданном пути. Величина этой скорости также известна как «номинальная скорость» (или «уравновешивающая скорость» для железных дорог) поворота или кривой.^[2] Обратите внимание, что номинальная скорость кривой одинакова для всех массивных объектов, а кривая без наклона будет иметь номинальную скорость 0.

Наклонный поворот с трением

Крутой поворот на съезд, ведущий на восток Маршрут штата Калифорния 92 на север Межгосударственный 880 в Хейворд, Калифорния.

Рассматривая влияние трения на систему, мы снова должны отметить, в какую сторону направлена ​​сила трения. При расчете максимальной скорости для нашего автомобиля трение будет указывать вниз по склону и к центру круга. Следовательно, мы должны добавить горизонтальную составляющую трения к нормальной силе. Сумма этих двух сил и составляет нашу новую чистую силу в направлении центра поворота (центростремительную силу):

${\displaystyle {mv^{2} \over r}=\mu _{s}N\cos \theta +N\sin \theta }$

Опять же, нет движения в вертикальном направлении, что позволяет нам установить все противостоящие вертикальные силы равными друг другу. Эти силы включают вертикальную составляющую нормальной силы, направленную вверх, и вес автомобиля, и вертикальную составляющую трения, направленную вниз:

${\displaystyle N\cos \theta =\mu _{s}N\sin \theta +mg}$

Решив приведенное выше уравнение для массы и подставив это значение в предыдущее уравнение, мы получим:

${\displaystyle {v^{2}\left(N\cos \theta -\mu _{s}N\sin \theta \right) \over rg}=\mu _{s}N\cos \theta +N\sin \theta }$

Решая относительно v, получаем:

${\displaystyle v={\sqrt {rg\left(\sin \theta +\mu _{s}\cos \theta \right) \over \cos \theta -\mu _{s}\sin \theta }}={\sqrt {rg\left(\tan \theta +\mu _{s}\right) \over 1-\mu _{s}\tan \theta }}}$

Это уравнение обеспечивает максимальную скорость для автомобиля с заданным углом наклона, коэффициент трения покоя и радиус кривизны. Подобным анализом минимальной скорости получается следующее уравнение:

${\displaystyle v={\sqrt {rg\left(\sin \theta -\mu _{s}\cos \theta \right) \over \cos \theta +\mu _{s}\sin \theta }}={\sqrt {rg\left(\tan \theta -\mu _{s}\right) \over 1+\mu _{s}\tan \theta }}}$

Разница в последнем анализе возникает при рассмотрении направления трения для минимальной скорости автомобиля (по направлению к внешней стороне круга). Следовательно, противоположные операции выполняются при подстановке трения в уравнения для сил в центростремительном и вертикальном направлениях.

Дорожные повороты с неправильным уклоном увеличивают риск выезда на бездорожье и лобовых столкновений. Можно ожидать, что 2% -ный недостаток виража (скажем, 4% -ный вираж на кривой, которая должна иметь 6%) увеличит частоту ДТП на 6%, а 5% -ный недостаток увеличит ее на 15%.^[3] До сих пор у дорожных инженеров не было эффективных инструментов для определения кривых с неправильным наклоном и разработки соответствующих мер по снижению воздействия на дорогах. Современный профилограф может предоставить данные как дороги кривизна и поперечный склон (угол наклона). Практическая демонстрация того, как оценивать повороты с неправильным наклоном, была разработана в проекте EU Roadex III. См. Связанный ссылочный документ ниже.

Наклонная очередь в воздухоплавании

Дуглас DC-3 кренинг, чтобы повернуть налево.

Когда самолет делает разворот (меняет направление), самолет должен перекатиться в положение крена, чтобы его крылья наклонены к желаемому направлению поворота. Когда разворот завершен, дрон должен откатиться до горизонтального положения крыльев, чтобы продолжить полет по прямой.^[4]

Когда любое движущееся транспортное средство делает поворот, необходимо, чтобы силы, действующие на транспортное средство, в сумме составляли чистую внутреннюю силу, чтобы вызвать центростремительное ускорение. В случае разворота самолета сила, вызывающая центростремительное ускорение, является горизонтальной составляющей поднимать действующий на самолет.

В прямом горизонтальном полете подъемная сила, действующая на самолет, действует вертикально вверх, чтобы противодействовать весу самолета, действующему вниз. Во время сбалансированного поворота с углом крена θ лифт действует под углом θ подальше от вертикали. Полезно разделить подъемную силу на вертикальную составляющую и горизонтальную составляющую. Если самолет должен продолжать горизонтальный полет (т. Е. С постоянным высота ), вертикальная составляющая должна по-прежнему равняться весу самолета, поэтому пилот должен немного оттянуть ручку. Общая (теперь наклонная) подъемная сила больше, чем вес самолета, поэтому вертикальный компонент может равняться весу. Горизонтальный компонент неуравновешен и, следовательно, является равнодействующая сила заставляя дрон ускоряться внутрь и выполнять разворот.

Векторная диаграмма, показывающая подъемную силу и вес, действующие на самолет с неподвижным крылом во время поворота с креном Изображенная желтая сила представляет собой результирующую силу, вызывающую центростремительное ускорение.

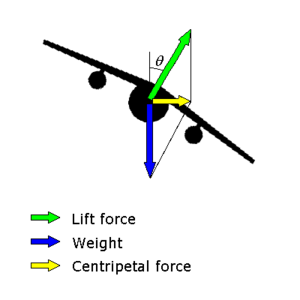
Потому что центростремительное ускорение:

${\displaystyle a={v^{2} \over r}}$

Второй закон Ньютона в горизонтальном направлении можно математически выразить как:

${\displaystyle L\sin \theta ={mv^{2} \over r}}$

куда:

L лифт, действующий на самолет

θ угол крена самолета

м это масса самолета

v это истинная воздушная скорость самолета

р это радиус поворота

В горизонтальном полете подъемная сила равна массе самолета. В разворотном полете подъемная сила превышает вес самолета и равна массе самолета (мг) делится на косинус угла крена:

${\displaystyle L={mg \over {\cos \theta }}}$

куда грамм - напряженность гравитационного поля.

Радиус поворота теперь можно рассчитать:^[5]

${\displaystyle r={v^{2} \over {g\tan \theta }}}$

Эта формула показывает, что радиус разворота пропорционален квадрату площади самолета. истинная воздушная скорость. При более высокой воздушной скорости радиус поворота больше, при более низкой воздушной скорости радиус меньше.

Эта формула также показывает, что радиус поворота уменьшается с увеличением угла крена. Чем больше угол крена, тем меньше радиус поворота, а с меньшим углом крена - больше.

В повороте с креном на постоянной высоте коэффициент нагрузки равно 1 / cosθ. Мы видим, что коэффициент нагрузки при прямом и горизонтальном полете равен 1, поскольку cos (0) = 1, и для создания достаточной подъемной силы для поддержания постоянной высоты коэффициент нагрузки должен приближаться к бесконечности, поскольку угол крена приближается к 90 °, а cosθ приближается к нулю. . Это физически невозможно, потому что конструктивные ограничения самолета или физическая выносливость пассажиров будут превышены задолго до этого.

Смотрите также

• Угол развала
• Не могу (автомобильный / железнодорожный)
• Сила Кориолиса (восприятие)
• Центростремительная сила
• перегрузка
• Овальные гонки на треке

Рекомендации

1. Serway, p. 143
2. Пиво, Фердинанд П.; Джонстон, Э. Рассел (11 июля 2003 г.). Векторная механика для инженеров: динамика. Наука / Инженерия / Математика (7-е изд.). Макгроу-Хилл. ISBN  978-0-07-293079-5.
3. Д.В. Харвуд и др., Прогноз ожидаемых показателей безопасности сельских двухполосных автомобильных дорог, Центр исследований шоссе Тернер-Фэйрбанк, Маклин, Вирджиния, декабрь 2000 г., стр. 39, http://www.fhwa.dot.gov/publications/research/safety/99207/99207.pdf
4. Федеральное управление гражданской авиации (2007 г.). Энциклопедия авиационных знаний пилотов. Оклахома-Сити ОК: Skyhorse Publishing Inc. Рисунок 3–21. ISBN  978-1-60239-034-8.
5. Клэнси, Л.Дж., Уравнение 14.9.

дальнейшее чтение

Наземная техника

• Серуэй, Раймонд. Физика для ученых и инженеров. Cengage Learning, 2010 г.
• Вопросы здоровья и безопасности, проект EU Roadex III по вопросам здоровья и безопасности, возникающим из-за плохого состояния дорожных сетей.

Аэронавтика

• Кермод, A.C. (1972) Механика полета, Глава 8, 10-е издание, Longman Group Limited, Лондон ISBN  0-582-23740-8
• Клэнси, Л.Дж. (1975), Аэродинамика, Pitman Publishing Limited, Лондон ISBN  0-273-01120-0
• Hurt, H.H. Jr, (1960), Аэродинамика для морских авиаторов, Перепечатка национального авиационного магазина, Флорида

внешняя ссылка

Наземная техника

• http://hyperphysics.phy-astr.gsu.edu/hbase/mechanics/imgmech/carbank.gif
• https://web.archive.org/web/20051222173550/http://whitts.alioth.net/
• http://www.batesville.k12.in.us/physics/PHYNET/Mechanics/Circular%20Motion/banked_no_friction.htm

Аэронавтика

• НАСА: Руководство по банковским поворотам
• aerospaceweb.org: угол крена и G (математика)
• Справочник пилота по аэронавигационным знаниям