Бинарная тетраэдрическая группа - Binary tetrahedral group

Регулярный сложный многогранник, 3 {6} 2 или или , представляет Диаграмма Кэли для бинарной тетраэдрической группы каждый красный и синий треугольник является направленным подграфом.^[1]

В математика, то бинарная тетраэдрическая группа, обозначаемый 2T или 2,3,3⟩, является некоторой неабелева группа из порядок 24. Это расширение из тетраэдрическая группа T или (2,3,3) порядка 12 на циклическая группа порядка 2, и является прообраз тетраэдрической группы под 2: 1 покрывающий гомоморфизм Спин (3) → SO (3) специальная ортогональная группа посредством вращательная группа. Отсюда следует, что бинарная тетраэдральная группа является дискретная подгруппа спина (3) порядка 24. комплексная группа отражений названо 3 (24) 3 по G.C. Шепард или 3 [3] 3 и от Coxeter, изоморфна бинарной тетраэдрической группе.

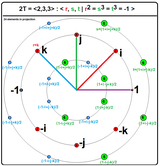
Бинарную тетраэдральную группу проще всего описать конкретно как дискретную подгруппу кватернионы единиц, при изоморфизме Отжим (3) ≅ Спин (1), где Sp (1) - мультипликативная группа единичных кватернионов. (Описание этого гомоморфизма см. В статье о кватернионы и пространственные вращения.)

Элементы

Граф Кэли SL (2,3)

Проекции симметрии

8-кратный	12-кратный
24 элемента кватерниона: 1 заказ-1: 1 1 заказ-2: -1 6 порядок-4: ± i, ± j, ± k 8 порядок-6: (+ 1 ± i ± j ± k) / 2 8 порядок-3: (-1 ± i ± j ± k) / 2.

Явно бинарная тетраэдральная группа задается как группа единиц в кольцо из Целые числа Гурвица. Всего таких единиц 24

${displaystyle {pm 1,pm i,pm j,pm k,{ frac {1}{2}}(pm 1pm ipm jpm k)}}$

со всеми возможными комбинациями знаков.

Все 24 единицы имеют абсолютное значение 1 и, следовательно, принадлежат к группе кватернионов единиц Sp (1). В выпуклая оболочка из этих 24 элементов в 4-мерном пространстве образуют выпуклый правильный 4-многогранник называется 24-элементный.

Свойства

Бинарная тетраэдрическая группа, обозначенная 2T, вписывается в короткая точная последовательность

${displaystyle 1 o {pm 1} o 2mathrm {T} o mathrm {T} o 1.}$

Эта последовательность не Трещина, что означает, что 2T не а полупрямой продукт группы {± 1} посредством T. На самом деле не существует подгруппы в 2T, изоморфной T.

Бинарная тетраэдральная группа - это группа покрытия тетраэдрической группы. Думая о тетраэдрической группе как о переменная группа на четыре буквы, Т ≅ А₄, таким образом, мы имеем бинарную группу тетраэдра как покрывающую группу, 2Т ≅ ${displaystyle {widehat {mathrm {A} _{4}}}}$.

В центр группы 2T является подгруппой {± 1}. В группа внутренних автоморфизмов изоморфна A₄, и полный группа автоморфизмов изоморфна S₄.^[2]

Левое умножение на -ω, порядок -6 элемент: посмотрите на серые, синие, фиолетовые и оранжевые шары и стрелки, которые составляют 4орбиты (две стрелки не изображены). ω сам по себе самый нижний шар: ω = (−ω)(−1) = (−ω)⁴

Бинарную тетраэдральную группу можно записать как полупрямой продукт

${displaystyle 2mathrm {T} =mathrm {Q} times mathrm {C} _{3}}$

где Q - группа кватернионов состоящий из 8 Единицы Липшица и C₃ это циклическая группа порядка 3, порожденного ω = −1/2(1 + я + j + k). Группа Z₃ действует на нормальную подгруппу Q формулой спряжение. Спряжение ω - автоморфизм Q, который циклически вращает я, j, и k.

Можно показать, что бинарная группа тетраэдра изоморфна группе специальная линейная группа SL (2,3) - группа всех 2 × 2 матрицы над конечное поле F₃ с единичным определителем, причем этот изоморфизм покрывает изоморфизм проективная специальная линейная группа PSL (2,3) с знакопеременной группой A₄.

Презентация

Группа 2T имеет презентация данный

${displaystyle langle r,s,tmid r^{2}=s^{3}=t^{3}=rstangle }$

или эквивалентно,

${displaystyle langle s,tmid (st)^{2}=s^{3}=t^{3}angle .}$

Генераторы с этими отношениями даются

${displaystyle r=kqquad s={ frac {1}{2}}(1+i+j+k)qquad t={ frac {1}{2}}(1+i+j-k).}$

С участием ${displaystyle r^{2}=s^{3}=t^{3}=-1}$

Подгруппы

В бинарная тетраэдрическая группа, 2T = <3,3,2>, имеет 2 первичные подгруппы:
* группа кватернионов, Q = <2,2,2>, индекс 3
* группа диэдра Z6 = <3>, индекс 4.

В группа кватернионов состоящий из 8 Единицы Липшица образует нормальная подгруппа 2Т из показатель 3. Эта группа и центр {± 1} - единственные нетривиальные нормальные подгруппы.

Все остальные подгруппы 2T являются циклические группы генерируется различными элементами с порядками 3, 4 и 6.^[3]

Высшие измерения

Так же, как группа тетраэдра обобщается на группу вращательной симметрии п-симплекс (как подгруппа SO (п)) существует соответствующая высшая бинарная группа, которая представляет собой 2-кратную оболочку, исходящую от оболочки Spin (п) → SO (п).

Группа вращательной симметрии п-симплекс можно рассматривать как переменная группа на п +1 балл, A_п+1, а соответствующая бинарная группа является двумерной группа покрытия. Для всех высших измерений, кроме A₆ и А₇ (соответствующие 5-мерному и 6-мерному симплексам) эта бинарная группа является группа покрытия (максимальное покрытие) и является суперсовершенный, но для размерностей 5 и 6 существует дополнительное исключительное 3-кратное покрытие, и бинарные группы не являются суперсовершенными.

Использование в теоретической физике

Бинарная тетраэдрическая группа использовалась в контексте Теория Янга – Миллса в 1956 г. Чен Нин Ян и другие.^[4]Впервые он был использован при построении модели физики ароматов Пол Фрэмптон и Томас Кефхарт в 1994 году.^[5]В 2012 году было показано ^[6] что связь между двумя углами смешивания нейтрино, полученная^[7]с использованием этой бинарной тетраэдрической симметрии аромата, согласуется с экспериментом.

Смотрите также

• Бинарная полиэдральная группа
• бинарная циклическая группа, ⟨п⟩, Порядок 2п
• бинарная группа диэдра, ⟨2,2,п⟩, Порядок 4п
• бинарная октаэдрическая группа, 2O = ⟨2,3,4⟩, порядок 48
• бинарная группа икосаэдра, 2I = ⟨2,3,5⟩, порядок 120

Заметки

1. Coxeter, Сложные правильные многогранники, стр 109, Рис. 11.5E
2. «Специальная линейная группа: SL (2,3)». группы.
3. SL₂(F₃) на GroupNames
4. Case, E.M .; Роберт Карплюс; C.N. Ян (1956). «Странные частицы и сохранение изотопного спина». Физический обзор. 101 (2): 874–876. Bibcode:1956ПхРв..101..874С. Дои:10.1103 / PhysRev.101.874.
5. Frampton, Paul H .; Томас В. Кефхарт (1995). «Простые неабелевы конечные ароматические группы и фермионные массы». Международный журнал современной физики. A10 (32): 4689–4704. arXiv:hep-ph / 9409330. Bibcode:1995IJMPA..10.4689F. Дои:10.1142 / s0217751x95002187.
6. Эби, Дэвид А .; Пол Х. Фрэмптон (2012). «Ненулевое значение тета (13) сигнализирует о немаксимальном смешении атмосферных нейтрино». Физический обзор. D86: 117–304. arXiv:1112.2675. Bibcode:2012PhRvD..86k7304E. Дои:10.1103 / Physrevd.86.117304.
7. Эби, Дэвид А .; Пол Х. Фрэмптон; Шинья Мацудзаки (2009). «Предсказания углов смешивания нейтрино в T ′ модели». Письма по физике. B671: 386–390. arXiv:0801.4899. Bibcode:2009ФЛБ..671..386Е. Дои:10.1016 / j.physletb.2008.11.074.

использованная литература

• Конвей, Джон Х.; Смит, Дерек А. (2003). О кватернионах и октонионах. Натик, Массачусетс: AK Peters, Ltd. ISBN  1-56881-134-9.
• Кокстер, Х. С. М. и Мозер, В. О. Дж. (1980). Генераторы и отношения для дискретных групп, 4-е издание.. Нью-Йорк: Springer-Verlag. ISBN  0-387-09212-9. 6.5. Бинарные группы полиэдров, с. 68