Капиллярные мостики - Capillary bridges - Wikipedia

Обычно мы понимаем термин капиллярный мостик как минимизированная поверхность жидкость или же мембрана, созданный между двумя твердыми телами произвольной формы. Между двумя жидкостями также могут образовываться капиллярные мостики.^[1] Плато определило последовательность форм капилляров.^[2] известный как (1) узловатый с 'шеей', (2) катеноид, (3) ундулоидный с 'шеей', (4) цилиндр, (5) ундулоидный с окорочком (6) сфера и (7) нодоид с 'окорочком'. Наличие капиллярных перемычек, в зависимости от их формы, может приводить к притяжению или отталкиванию между твердыми телами. Самые простые из них - осесимметричные. Мы выделили три важных класса перемычек в зависимости от формы поверхностей соединенных тел:

• две плоские поверхности (рис.1)

рис.1 Вогнутый капиллярный мостик между двумя плоскостями (схематическое изображение)

• плоская поверхность и сферическая частица (рис.2)

рис.2 Вогнутый капиллярный мостик между частицами и плоской поверхностью (схематическое изображение)

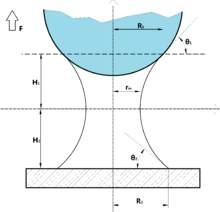
• две сферические частицы (как правило, частицы не могут быть одинакового размера, рис.3)

рис.3 Вогнутый капиллярный мостик между двумя частицами (схематическое изображение)

На капиллярные мостики и их свойства также могут влиять Земная гравитация и свойствами перекрываемых поверхностей. Связующее вещество может быть жидкостью или газом. Вмещающая граница называется интерфейсом (капиллярная поверхность ). Интерфейс отличается особым поверхностное натяжение.

История

Капиллярные мостики изучаются более 200 лет. Впервые вопрос был поставлен Йозеф Луи Лагранж в 1760 году, и интерес французского астронома и математика К. Делоне.^[3] Делоне обнаружил совершенно новый класс аксиально-симметричных поверхностей постоянная средняя кривизна. Формулировка и доказательство его теоремы имели долгую историю. Это началось с Эйлера^[4] предложение новой фигуры, называемой катеноид. (Намного позже Кенмоцу ^[5] решал сложные нелинейные уравнения, описывающие этот класс поверхностей. Однако его решение не имеет большого практического значения, поскольку не имеет геометрической интерпретации.) Ж. Плато показал существование таких форм с заданными границами. Проблема была названа его именем Проблема плато.^[6]
Многие ученые внесли свой вклад в решение проблемы. Один из них - Томас Янг.^[7] Пьер Симон Лаплас внес идею капиллярного напряжения. Лаплас даже сформулировал широко известное в настоящее время условие механического равновесия между двумя жидкостями, разделенными капиллярной поверхностью. п_γ= Δп то есть капиллярное давление между двумя фазами уравновешивается их соседней разницей давления.
Общий обзор поведения капиллярных мостиков в гравитационном поле завершен Мышкисом и Бабским.^[8]
В прошлом веке много усилий было направлено на изучение поверхностных сил, которые управляют капиллярными эффектами образования мостиков. Было установлено, что эти силы являются результатом межмолекулярных сил и становятся значительными в тонких жидкостных зазорах (<10 нм) между двумя поверхностями.^[9][10]
Неустойчивость капиллярных мостов впервые обсуждалась Рэлей.^[11] Он продемонстрировал, что струя жидкости или капиллярная цилиндрическая поверхность становятся неустойчивыми, когда соотношение между ее длиной ЧАС в радиус р, становится больше 2π. В этих условиях малых синусоидальных возмущений с длиной волны, превышающей его периметр, площадь поверхности цилиндра становится больше, чем у невозмущенного цилиндра того же объема, и поэтому он становится нестабильным. Позже Хоув ^[12] сформулированы вариационные требования к устойчивости осесимметричных капиллярных поверхностей (неограниченных) в отсутствие силы тяжести и с возмущениями, ограниченными постоянным объемом. Он первым решил уравнение Юнга-Лапласа для равновесных форм и показал, что условие Лежандра для второй вариации всегда выполняется. Следовательно, устойчивость определяется отсутствием отрицательного собственного значения линеаризованного уравнения Юнга-Лапласа. Этот подход определения устойчивости по второй вариации сейчас широко используется.^[8] Методы возмущений стали очень успешными, несмотря на то, что нелинейный характер капиллярного взаимодействия может ограничивать их применение. Другие методы теперь включают прямое моделирование.^[13][14] К тому моменту большинство методов определения устойчивости требовали расчета равновесия как основы для возмущений. Возникла новая идея, что устойчивость может быть выведена из состояний равновесия.^[15][16] Предложение было дополнительно доказано Питтсом.^[17] для осесимметричного постоянного объема. В последующие годы Фогель^[18][19] расширил теорию. Он исследовал случай осесимметричных капиллярных мостиков с постоянным объемом, и изменения устойчивости соответствуют точкам поворота. Недавнее развитие теории бифуркаций доказало, что обмен стабильности между точками поворота и точками ветвления - обычное явление.^[20][21]

Приложения и случаи

Недавние исследования показали, что древние египтяне использовали свойства песка для создания капиллярных мостиков с помощью воды.^[22] Таким образом они уменьшали поверхностное трение и были способны перемещать статуи и тяжелые камни пирамид. Некоторое современное искусство, например песочное искусство, также тесно связаны со способностью воды связывать частицы. В атомно-силовая микроскопия, когда человек работает в условиях повышенной влажности, на его исследования может повлиять появление наноразмерных капиллярных мостиков.^[23] Эти перемычки возникают при приближении рабочего наконечника к исследуемому образцу. Капиллярные мостики также играют важную роль в пайка процесс.^[24]

• 

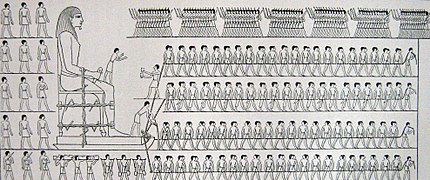
  Схема из гробницы Джехутихотеп с изображением транспорта колоссальной статуи

• 

  AFM

• 

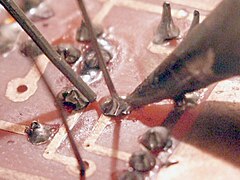
  Пайка

• 

  Древесная лягушка с белыми губами

Капиллярные мостики также широко распространены в живой природе. Жуки, мухи, кузнечики и древесные лягушки способны прилипать к вертикальным шероховатым поверхностям из-за их способности впрыскивать смачивающую жидкость в зону контакта подушечки с субстратом. Таким образом создается дальнодействующее привлекательное взаимодействие за счет образования капиллярных мостиков.^[25] Многие медицинские проблемы, связанные с респираторными заболеваниями, и здоровье суставов тела зависят от крошечных капиллярных мостиков.^[26] Жидкие мостики теперь широко используются при выращивании культур клеток из-за необходимости имитировать работу живых тканей в научных исследованиях.^[27][28]

Общие уравнения

Общее решение для профиля капилляра известно из рассмотрения ундулоидный или же узловатый кривизна.^[29]
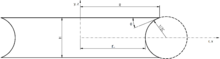
Предположим следующую цилиндрическую систему координат: z показывает ось вращения; р представляет радиальную координату и φ угол между нормалью и положительным z ось. Нодоид имеет вертикальные касательные в точках р = р₁ и р = р₂ и горизонтальная касательная в р = р₃. Когда φ угол между нормалью к границе и положительным z ось тогда φ равен 90 °, 0 °, -90 ° для нодоида.

В Уравнение Юнга-Лапласа можно записать в форме, удобной для интегрирования для осевой симметрии:

${\displaystyle \Delta P=\gamma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)=\gamma {\frac {d\left(r\sin \phi \right)}{rdr}}={\rm {constant}},}$

(1)

куда р₁, р₂ - радиусы кривизны и γ межфазное поверхностное натяжение.
Интегрирование уравнения называется первый интеграл и это дает:

${\displaystyle \sin \phi ={\frac {\left(r^{2}-r_{1}r_{2}\right)}{r\left(r_{1}-r_{2}\right)}}}$

(2)

С:

${\displaystyle {\frac {dz}{dr}}=-\tan \phi =-{\frac {\sin \phi }{\sqrt {\left(1-\sin ^{2}\phi \right)}}}}$

(3)

Обнаруживается:

${\displaystyle {\frac {dz}{dr}}={\frac {r_{1}r_{2}-r^{2}}{\sqrt {\left(r^{2}-r_{1}^{2}\right)\left(r_{2}^{2}-r^{2}\right)}}}}$

(4)

После интегрирования полученное уравнение называется второй интеграл:

${\displaystyle z=\pm \left[r_{1}F\left(r,\phi \right)-r_{2}E\left(r,\phi \right)\right]+{\frac {\sqrt {\left(1-{\frac {r_{0}^{2}}{r^{2}}}\right)\left({\frac {r_{1}^{2}}{r^{2}}}-1\right)}}{r}}}$

(5)

где: F и E - эллиптические интегралы первого и второго рода, ${\textstyle k^{2}={\frac {r_{1}^{2}-r_{2}^{2}}{r_{1}^{2}}}}$ и φ связана с r согласно

${\displaystyle \sin ^{2}\phi ={\frac {r^{2}-r_{2}^{2}}{k^{2}r^{2}}}}$.

У ундулоида есть только вертикальные касательные на р=р₁ и р=р₂, куда φ = + 90. Совершенно аналогично:

${\displaystyle {\frac {dz}{dr}}={\frac {r_{1}r_{2}+r^{2}}{\sqrt {\left(r^{2}-r_{1}^{2}\right)\left(r_{2}^{2}-r^{2}\right)}}}}$

(6)

Второй интеграл для ундулоида получается:

${\displaystyle z=\pm \left[r_{1}F\left(r,\phi \right)+r_{2}E\left(r,\phi \right)\right]+{\frac {\sqrt {\left(1-{\frac {r_{0}^{2}}{r^{2}}}\right)\left({\frac {r_{1}^{2}}{r^{2}}}-1\right)}}{r}}}$

(7)

где связь между параметрами k и φ определяется так же, как и выше. В предельном случае р₁= 0, и нодоид, и ундулоид состоят из серии сфер. Когда р₁=р₂. Последний и очень интересный предельный случай: катеноид. Уравнение Лапласа сводится к:

${\displaystyle {\frac {d\left(r\sin r\right)}{rdr}}=0}$

(8)

Его интегрирование можно представить в очень удобной форме в цилиндрической системе координат, называемой цепное уравнение:^[29]

${\displaystyle {\frac {r}{r_{1}}}=\cosh \left({\frac {z}{r_{1}}}\right)}$

(9)

Рис. 4. Область существования катеноидов (1) высота масштабируется по радиусу R, (2) высота масштабируется по кубическому корню из объема (действительно только для капиллярных перемычек C = 0)

Уравнение (9) важно, потому что оно показывает в некотором упрощении все вопросы, связанные с капиллярными мостиками, прозрачными. Чертежи в безразмерных координатах имеют максимум, что выделяет две ветви. Один из них энергетически выгоден и проявляется в статике, а другой (пунктирная линия) не является энергетически выгодным. Максимум важен, потому что при растяжении квазиравновесным способом капиллярного моста, если он достигается, происходит его разрыв. Катеноиды с энергетически невыгодными размерами могут образовываться в процессе динамического растяжения / сжатия.^[30] Нулевое капиллярное давление C= 0 естественно для классического катеноида (поверхность капиллярного мыла, натянутого между двумя коаксиальными кольцами). Когда типичный капиллярный мостик переходит в катеноидное состояние C = 0, несмотря на то, что свойства его поверхности такие же, как у классического катеноида, его более уместно представить в масштабе кубического корня из его объема, а не радиуса, р.

Решение второй интеграл отличается в случаях сплюснутых капиллярных мостиков (узловых и ундулоидных):

${\displaystyle z=\pm \left[r_{2}F\left(r,\phi \right)-\left(C-1\right)r_{2}E\left(r,\phi \right)\right]}$

(10)

где: F и E - снова эллиптические интегралы первого и второго рода, ${\textstyle k^{2}={\frac {r_{2}^{2}-r_{1}^{2}}{r_{2}^{2}}}}$ а φ связана с r согласно: ${\textstyle \sin ^{2}\phi ={\frac {r_{2}^{2}-r^{2}}{k^{2}r_{2}^{2}}}}$.
Важно отметить, что все описанные кривые получены прокаткой конического участка без скольжения по z ось. Ундулоид описывается фокусом катящегося эллипса, который может вырождаться в линию, сферу или параболу, что приводит к соответствующим предельным случаям. Точно так же нодоид описывается фокусом катящейся гиперболы.

Хорошо систематизированная сводка форм капиллярных мостиков приведена в таблице 11.1 книги Кральчевского и Нагаямы.^[2]

Статика между двумя плоскими поверхностями

Механическое равновесие включает баланс давления на границе раздела жидкость / газ и внешнюю силу на пластинах Δп, уравновешивая капиллярное притяжение или отталкивание, ${\displaystyle P_{\gamma }}$, т.е. ${\displaystyle \Delta P=P_{\gamma }}$. В пренебрежении гравитационными эффектами и другими внешними полями баланс давления равен Δп=п_я - п_е (Индексы «i» и «e» обозначают соответственно внутреннее и внешнее давление). В случае аксиальной симметрии уравнение капиллярного давления принимает вид:

${\displaystyle P_{\gamma }=\gamma {\frac {d(r\sin {\phi })}{rdr}}}$

(11)

куда γ - межфазное натяжение жидкость / газ; р - радиальная координата и φ - угол между осью симметрии и нормалью к образующей интерфейса.
Первый интеграл легко получить относительно безразмерного капиллярного давления при контакте с поверхностью:

${\displaystyle C={\frac {X\sin {\theta }-1}{X^{2}-1}}}$

(12)

куда ${\textstyle C=P_{\gamma }{\frac {r_{m}}{2\gamma }}}$, безразмерный радиус на контакте равен ${\textstyle X={\frac {R}{r_{m}}}}$ и θ угол смачивания. Соотношение показывает, что капиллярное давление может быть положительным или отрицательным. Форма капиллярных мостиков определяется уравнением:^[2]

${\displaystyle {\frac {dy}{dx}}=\pm {\frac {C\left(x^{2}-1\right)+1}{\sqrt {x^{2}-\left[C\left(x^{2}-1\right)+1\right]^{2}}}}}$

(13)

где уравнение получается после подстановки ${\textstyle \sin \phi ={\frac {dy}{dx}}\cos \phi }$ сделан в формуле. (11) и скрежет ${\textstyle x={\frac {r}{r_{m}}}}$ вводится.

Тонкий жидкий мостик

В отличие от случаев увеличения высоты капиллярных перемычек, что предполагает разнообразие форм профиля, уплощение (утонение) до нулевой толщины имеет гораздо более универсальный характер. Универсальность появляется, когда ЧАС<<р (рисунок 1). Уравнение (11) можно записать:^[31]

${\displaystyle C\left(X=1-\Delta \right)\approx -{\frac {1-\sin \theta }{2\Delta }}+{\frac {1+\sin \theta }{4}}}$

(14)

Образующая сходится к уравнению:

${\displaystyle {\frac {dy}{dx}}=\pm {\frac {1+2C\left(x-1\right)}{\sqrt {1-\left[2C\left(x-1\right)+1\right]^{2}}}}}$

(15)

После интегрирования уравнение дает:

рис.5. Тонкий жидкий мостик

${\displaystyle y^{2}+\left(x+1\pm {\frac {1}{2C}}\right)^{2}=\left({\frac {1}{2C}}\right)^{2}}$

(16)

Безразмерный круговой радиус 1 / 2C совпадает с радиусом кривизны капиллярного мостика. Положительный знак «+» представляет профиль образующей вогнутой перемычки, а отрицательный «-» - сжатый. Для выпуклых капиллярных перемычек круговая образующая сохраняется до достижения границы области определения при растяжении. Ближе к началу кинетики самоинициируемого разрушения профиль перемычки эволюционирует, следовательно, в эллипс, параболу и, возможно, в гиперболу.^[32]

Домен определения

Наблюдения, представленные на рис. 5 указывают на то, что область существования капиллярных мостиков может быть определена. Следовательно, при растяжении жидкого мостика он может прекратить свое существование не только из-за повышения нестабильности, но и из-за достижения некоторых точек, в которых форма больше не может существовать. Оценка области определения требует манипулирования интегральными уравнениями для высоты капиллярного мостика и его объема. Оба они интегрируемы, но интегралы несобственные. Применяемый метод включает разбиение интегралов на две части: сингулярную, но аналитически интегрируемую, и регулярную, но интегрируемую только численно.
После интегрирования для капиллярного мостика получается высота^[31]

${\displaystyle H^{*}\equiv \left({\frac {H}{\sqrt[{3}]{V}}}\right)={\frac {1}{X}}\left({\frac {R}{\sqrt[{3}]{V}}}\right)\left\{{\frac {\pi }{4C}}-\alpha \left(X,C\right)-\int \limits _{1}^{X}{\sqrt {\frac {\zeta -C\left(X^{2}-1\right)+1}{\zeta +C\left(X^{2}-1\right)+1}}}d\zeta \right\}}$

(17)

Аналогичный способ для радиуса контакта р, получается интегральное уравнение^[31]

${\displaystyle R^{*}\equiv \left({\frac {R}{\sqrt[{3}]{V}}}\right)={\frac {X}{\sqrt[{3}]{2\pi }}}\left\{\beta \left(C\right){\frac {\pi }{4C}}-{\frac {\sqrt {\left(1-2C\right)\left(X^{2}-1\right)}}{2C^{2}}}-\beta \left(C\right)\alpha \left(X,C\right)-\int \limits _{1}^{X}\zeta ^{2}{\sqrt {\frac {\zeta -C\left(X^{2}-1\right)+1}{\zeta +C\left(X^{2}-1\right)+1}}}d\zeta \right\}^{-{\frac {1}{3}}}}$

(18)

куда ${\displaystyle \beta \left(C\right)=\left[1-{\frac {\left(1-2C\right)}{2C^{2}}}\right]}$ и ${\displaystyle \alpha \left(C,X\right)={\frac {1}{2C}}\arcsin \left[\beta \left(C\right)-X^{2}{\frac {2C^{2}}{1-2C}}\right]}$

Рис. 6. Изогоны демонстрируют статический домен капиллярных мостиков, красная кривая показывает катеноидальное состояние C = 0.

На рис. 6 показано количество устойчивых статических состояний жидкого капиллярного мостика, представленных двумя характерными параметрами: (i) безразмерная высота, которая получается путем масштабирования высоты капиллярного мостика на кубический корень из его объема Ур. (16) и (ii) его радиус, также масштабированный на кубический корень из объема, уравнение. (17). Частично аналитические решения, полученные для этих двух параметров, представлены выше. Решения чем-то отличаются от общепринятого подхода Плато [эллиптическими функциями, уравнение. (7)], поскольку они предлагают удобный численный подход для интегрирования регулярных интегралов, а нерегулярная часть уравнения интегрирована аналитически. Эти решения стали в дальнейшем основой для предсказания квазиравновесного растяжения и разрушения капиллярных мостиков при углах смачивания менее 45 °.${\textstyle \left(0\leq \theta \leq {\frac {\pi }{4}}\right)}$. Практическая реализация позволяет идентифицировать не только конец области определения, но и точное поведение при растяжении капиллярного мостика,^[32] потому что в координатах ${\textstyle {\frac {H}{r_{m}}}\sim \ln \left({\frac {R}{r_{m}}}\right)}$ при растяжении образуется наклонная линия, угол наклона которой пропорционален углу смачивания.

Вогнутый капиллярный мостик

Случай вогнутого капиллярного мостика представлен изогонами для углов смачивания ниже ${\textstyle {\frac {\pi }{2}}}$ на рис. 6, ${\textstyle \left(0\leq \theta <{\frac {\pi }{2}}\right)}$. Изогоны показывают хорошо выраженный максимум ${\textstyle {\frac {dH^{*}}{dR^{*}}}\equiv {\frac {dH}{dR}}=0}$. Этот максимум отмечен точкой для каждой изогоны. Он снова, как и простой катеноид, разделяет две ветви. Левая ветвь энергетически выгодна, а правая - энергетически невыгодна.

Цилиндрический капиллярный мост

Этот случай хорошо проанализирован Рэлеем. Обратите внимание, что область определения в его случае не имеет ограничений и уходит в бесконечность, рис. 6, ${\textstyle \left(\theta ={\frac {\pi }{2}}\right)}$. Однако обычно наблюдается разрыв цилиндрических капиллярных перемычек. Это происходит в результате хорошо изученной нестабильности, известной сейчас как Неустойчивость Рэлея.^[11] Область определения для изогоны 90 ° показана на рис. 6 пунктирной линией.

Выпуклый капиллярный мостик

Случай выпуклых капиллярных перемычек представлен на рис. 6, ${\textstyle \left({\frac {\pi }{2}}<\theta \leq \pi \right)}$ слева от области цилиндрического корпуса.

Устойчивость между двумя плоскими поверхностями

Формы равновесия и пределы устойчивости капиллярных жидких мостиков являются предметом многих теоретических и экспериментальных исследований.^[33] Исследования в основном сосредоточены на изучении мостов между равными дисками в условиях гравитации. Как известно, для каждого значения Номер облигации, определяется как^[34] ${\textstyle {\rm {Bo}}={\frac {\rho gR^{2}}{\gamma }}}$ (куда: грамм - ускорение свободного падения Земли, γ поверхностное натяжение и р - радиус контакта) диаграмму устойчивости можно представить в виде единственной замкнутой кусочной кривой на плоскости гибкость / безразмерный объем. Стройность определяется как ${\textstyle {\frac {H}{2R}}}$, а безразмерный объем - это объем капиллярного мостика, деленный на объем цилиндра одинаковой высоты, ЧАС и радиус р: ${\textstyle {\frac {V}{\pi R^{2}H}}}$.

Если и гибкость, и объем жидкости достаточно малы, пределы устойчивости регулируются отрывом жидкой формы от краев дисков (линия трехфазного контакта), линия AB на рис. 7. Линия BC представляет минимум объема, соответствующий осесимметричному разрушению. В литературе он известен как минимальная стабильность объема предел. Кривая CA представляет собой еще один предел стабильности, характеризующий максимальный объем. Это верхняя граница области устойчивости. Также существует переходная область между минимальной и максимальной стабильностью объема. Он еще не определен четко и поэтому отмечен пунктирной линией на рис. 7.^{[куда? ]}

Смотрите также

• Число Этвёша
• Капиллярная конденсация

Рекомендации

1. Росс, Сидней (1950). «Ингибирование пенообразования. II. Механизм разрыва жидких пленок противовспенивающими агентами». J. Phys. Chem. 54 (3): 429–436. Дои:10.1021 / j150477a018.
2. Кральчевский, П .; Нагаяма, К. (2001). Частицы на границах раздела жидкостей и мембранах. Амстердам: Эльзевир. С. 469–502.
3. Делоне (1841 г.). "Sur la Surface de Revolution dont la Courbure Moyenne est Constante". J. Math. Pures Appl. 6: 309–314.
4. Л. Эйлер, Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, Opera omnia, I, 24, (1744)
5. Кенмоцу К. Поверхности вращения с заданной средней кривизной // Tohoku Math. J. 32 (1980), 147–153.
6. Плато, Йозеф (1873 г.). Statique expérimentale et théorique des liquides soumis aux seulesforces moléculaires. Готье-Виллар.
7. Янг, Т. (1805). «Эссе о сцеплении жидкостей». Филос. Пер. R. Soc. Лондон. 95: 65–87. Дои:10.1098 / рстл.1805.0005.
8. Мышкис А. Бабский, Механика малогравитационной жидкости: математическая теория капиллярных явлений, Springer-Verlag, 1987.
9. Николай В. Чураев, Б.В. Дерягин, В. Мюллер, Поверхностные силы, Springer Scoence and Business Media, 1987 г.
10. Дж. Исраэлашвилли, Межмолекулярные и поверхностные силы, Третье издание: переработанное, Elsevier, 2011 г.
11. Страт, Дж. У., лорд Рэлей, О нестабильности струй, Слушания Лондонского математического общества, т. 10, стр. 4-13 (1878)
12. Хоув, В., доктор философии. Диссертация, Friendlich-Wilhelms, Universitat zu Berlin (1887)
13. Meseguer, J .; Санс, А. (1985). «Численное и экспериментальное исследование динамики осесимметричных жидких мостов».. J. Жидкий мех. 153: 83. Дои:10.1017 / s002211208500115x.
14. Мартинес; Пералес, Дж. М. (1986). «Данные об устойчивости жидкого мостика». J. Cryst. Рост. 78 (2): 369. Bibcode:1986JCrGr..78..369M. Дои:10.1016/0022-0248(86)90073-4.
15. Дж. Ф. Паддей, А. Р.Питт, Стабильность осесимметричных менисков, Философские труды Королевского общества A, (1973)
16. Boucher, E. A .; Эванс, М. Дж. Б. (1975). «Профили висящих капель и связанные с ними капиллярные явления». Труды Лондонского королевского общества A: математические и физические науки. 346 (1646): 349–374. Bibcode:1975RSPSA.346..349B. Дои:10.1098 / rspa.1975.0180.
17. Питтс Р., Устойчивость капли, свисающей с трубы, IMA J Appl Math (1976) 17 (3): 387-397.
18. Фогель, Томас И., Стабильность капли жидкости, зажатой между двумя параллельными плоскостями, SIAM J. Appl. Математика. 47 (1987), 516–525
19. Фогель, Томас И., Стабильность капли жидкости, зажатой между двумя параллельными плоскостями II, SIAM J. Appl. Математика. 49 (1989), 1009–1028.
20. Майкл Д. Х., Annual Review of Fluid Mechanics Vol. 13: 189-216 (дата публикации тома январь 1981 г.)
21. Брайан Джеймс, Лоури; Стин, Пол Х. (1995). «Капиллярные поверхности: устойчивость из семейств равновесий в приложении к жидкостному мосту». Труды Королевского общества А. 449 (1937): 411–439. Bibcode:1995RSPSA.449..411L. Дои:10.1098 / RSPA.1995.0051.
22. А. Фолл, Б. Вебер, М. Пакпур, Н. Ленуар, Н. Шахидзаде, Дж. Фисцина, К. Вагнер и Д. Бонн, Трение скольжения на влажном и сухом песках Phys. Rev. Lett. 112, 175502, опубликовано 29 апреля 2014 г.
23. Юмэй Мэнь, Сяньжэнь Чжан и Вэньчуань Ван, Капиллярные жидкие мостики в атомно-силовой микроскопии (АСМ): образование, разрыв и гистерезис, J. Chem. Phys. 131, 184702 (2009).
24. Ft. Б. ЭДВАРДС, Совместные допуски в соединениях капиллярных медных трубопроводов, Welding Journal, v06, pp 321- (1972)
25. Перссон, Б. Н. Дж. (2007). «Мокрая адгезия с нанесением на подушечки пальцев ног древесных лягушек и шины». J. Phys .: Condens. Иметь значение. 19 (37): 376110. Bibcode:2007JPCM ... 19K6110P. Дои:10.1088/0953-8984/19/37/376110. S2CID  73607791.
26. Alencar, A.M .; Majumdar, A .; Hantos, Z .; Булдырев, С.В .; Stanley, H.E .; Суки, Б. (2005). «Хрипы и нестабильность при вздутии легких». Physica A. 357: 18–26. Bibcode:2005PhyA..357 ... 18А. Дои:10.1016 / j.physa.2005.05.047.
27. Pampaloni, F .; Reynaud, E.G .; Stelzer, E.H.K. (2007). «Третье измерение ликвидирует разрыв между культурой клеток и живой тканью». Обзоры природы Молекулярная клеточная биология. 8 (10): 839–845. Дои:10.1038 / nrm2236. PMID  17684528.
28. Дж. Дилизи, Р. Демпси, Р. Рарик и К. Розенблатт, Использование параболических полетов для количественного исследования устойчивости жидких мостов при изменении общей силы тела, Sci. и Тех. (Отправлено)
29. Принсен Н.М., "Равновесная форма границ раздела, капель и пузырей, жесткие и деформируемые частицы на границах раздела" в науке о поверхности и коллоидах, под ред. Э. Матиджиевич, (1969), т.3, Нью-Йорк
30. Масато Ито, Таку Сато, Наблюдение на месте катеноида мыльной пленки - простой образовательный физический эксперимент, Eur. J. Phys. 31 (2010) 357-365
31. Петков, П.В .; Радоев, Б. Р. (2014). «Статика и динамика капиллярных мостов». Коллоиды и поверхности A: Physicochem. Англ. Аспекты. 460: 18–27. Дои:10.1016 / j.colsurfa.2014.03.038.
32. Петков, П.В .; Радоев, Б. Р. (2019). «Исследование одиночных и двойных выпуклых жидких капиллярных мостиков типа« сэндвич », натянутых между двумя плоскими поверхностями (экспериментальный подход)». Коллоидные интерфейсы. 3 (68): 68. Дои:10,3390 / коллоиды 3040068.
33. Безденежных, Н. А .; Meseguer, J .; Пералес, Дж. М. (1992). «Экспериментальный анализ пределов устойчивости капиллярных жидких мостиков». Phys. Жидкости А. 4 (4): 677. Bibcode:1992ФФЛА ... 4..677Б. Дои:10.1063/1.858286.
34. Ши, З .; и другие. (2018). «Гистерезис динамического краевого угла в жидкостных мостах». Коллоиды и поверхности A: физико-химические и технические аспекты. 555: 365–371. arXiv:1712.04703. Дои:10.1016 / j.colsurfa.2018.07.004.