Соединение десяти октаэдров - Compound of ten octahedra

Соединения десяти октаэдров
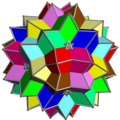Тип	Равномерное соединение
Индекс	UC15 и UC16
Многогранники	10 октаэдры
Лица	20+60 треугольники
Края	120
Вершины	60
Группа симметрии	икосаэдр (ячас)
Подгруппа ограничиваясь одной составляющей	3-кратный антипризматический (D3D)

3D-модель соединения десяти октаэдров UC₁₅

3D-модель соединения десяти октаэдров UC₁₆

В соединения десяти октаэдров UC₁₅ и UC₁₆ два однородные многогранники. Они состоят из симметричного расположения 10 октаэдры, считается треугольным антипризмы, совмещенных с осями тройной вращательной симметрии икосаэдр. Два соединения различаются ориентацией своих октаэдров: каждое соединение может быть преобразовано в другое, вращая каждый октаэдр на 60 градусов.

Декартовы координаты

Декартовы координаты для вершин этого соединения - все циклические перестановки

(0, ± (τ⁻¹√2 + 2sτ), ± (τ√2 - 2сτ⁻¹))

(±(√2 − sτ²), ±(√2 + s(2τ - 1)), ± (√2 + sτ⁻²))

(± (τ⁻¹√2 − sτ), ± (τ√2 + sτ⁻¹), ±3s)

где τ = (1 + √5) / 2 - это Золотое сечение (иногда пишется φ) и s равно +1 или -1. Настройка s = −1 дает UC₁₅, в то время как s = +1 дает UC₁₆.

Смотрите также

• Соединение трех октаэдров
• Соединение четырех октаэдров
• Соединение пяти октаэдров
• Соединение двадцати октаэдров

Рекомендации

• Скиллинг, Джон (1976), "Равномерные соединения однородных многогранников", Математические труды Кембриджского философского общества, 79: 447–457, Дои:10.1017 / S0305004100052440, Г-Н  0397554.