Функция Coshc - Coshc function - Wikipedia

В математике Функция Coshc часто появляется в статьях об оптическом рассеянии,^[1] Пространство-время Гейзенберга^[2] и гиперболическая геометрия.^[3] Он определяется как^[4][5]

${\displaystyle \operatorname {Coshc} (z)={\frac {\cosh(z)}{z}}}$

Это решение следующего дифференциального уравнения:

${\displaystyle w(z)z-2{\frac {d}{dz}}w(z)-z{\frac {d^{2}}{dz^{2}}}w(z)=0}$

Сюжет Coshc 2D

Coshc '(z) 2D график

Мнимая часть в комплексной плоскости

• ${\displaystyle \operatorname {Im} \left({\frac {\cosh(x+iy)}{x+iy}}\right)}$

Реальная часть в комплексной плоскости

• ${\displaystyle \operatorname {Re} \left({\frac {\cosh(x+iy)}{x+iy}}\right)}$

абсолютная величина

• ${\displaystyle \left|{\frac {\cosh(x+iy)}{x+iy}}\right|}$

Производная первого порядка

• ${\displaystyle {\frac {\sinh(z)}{z}}-{\frac {\cosh(z)}{z^{2}}}}$

Реальная часть производной

• ${\displaystyle -\operatorname {Re} \left(-{\frac {1-(\cosh(x+iy))^{2}}{x+iy}}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}}\right)}$

Мнимая часть производной

• ${\displaystyle -\operatorname {Im} \left(-{\frac {1-(\cosh(x+iy))^{2}}{x+iy}}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}}\right)}$

абсолютное значение производной

• ${\displaystyle \left|-{\frac {1-(\cosh(x+iy))^{2}}{x+iy}}+{\frac {\cosh(x+iy)}{(x+iy)^{2}}}\right|}$

Что касается других специальных функций

• ${\displaystyle \operatorname {Coshc} (z)={\frac {(iz+1/2\,\pi ){\rm {M}}(1,2,i\pi -2z)}{{\rm {e}}^{(i/2)\pi -z}z}}}$

• ${\displaystyle \operatorname {Coshc} (z)={\frac {1}{2}}\,{\frac {(2\,iz+\pi )\operatorname {HeunB} \left(2,0,0,0,{\sqrt {2}}{\sqrt {1/2\,i\pi -z}}\right)}{{\rm {e}}^{1/2\,i\pi -z}z}}}$

• ${\displaystyle \operatorname {Coshc} (z)={\frac {-i(2\,iz+\pi ){{\rm {\mathbf {W} hittakerM}}(0,\,1/2,\,i\pi -2z)}}{(4iz+2\pi )z}}}$

Расширение серии

${\displaystyle \operatorname {Coshc} z\approx \left(z^{-1}+{\frac {1}{2}}z+{\frac {1}{24}}z^{3}+{\frac {1}{720}}z^{5}+{\frac {1}{40320}}z^{7}+{\frac {1}{3628800}}z^{9}+{\frac {1}{479001600}}z^{11}+{\frac {1}{87178291200}}z^{13}+O(z^{15})\right)}$

Приближение Паде

${\displaystyle \operatorname {Coshc} \left(z\right)={\frac {23594700729600+11275015752000\,{z}^{2}[phone]\,{z}^{4}[phone]\,{z}^{6}[phone]\,{z}^{8}}{147173\,{z}^{9}-39328920\,{z}^{7}[phone]\,{z}^{5}-522334612800\,{z}^{3}[phone]\,z}}}$

Галерея

Coshc abs комплекс 3D

Coshc Im сложный 3D сюжет

Coshc Re сложный 3D сюжет

Coshc '(z) Im сложный 3D-сюжет

Coshc '(z) Re сложный 3D сюжет

Комплексный трехмерный сюжет Coshc '(z) abs

График плотности абс '(x) абс

График плотности Coshc '(x) Im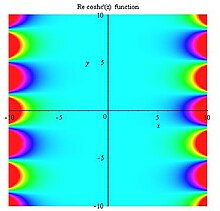

График плотности Coshc '(x) Re

Смотрите также

• Функция Tanc
• Функция Tanhc
• Функция sinhc

Рекомендации

1. PN Den Outer, TM Nieuwenhuizen, A. Lagendijk, Местоположение объектов в многократно рассеивающих средах, JOSA A, Vol. 10, выпуск 6, стр. 1209–1218 (1993)
2. Т. Корпинар, Новые характеристики для минимизации энергии бигармонических частиц в пространстве-времени Гейзенберга, Международный журнал теоретической физики, 2014 г., Springer
3. Нильгюн Сёнмез, Тригонометрическое доказательство теоремы Эйлера в гиперболической геометрии, Международный математический форум, 4, 2009, вып. 38, 1877 1881
4. JHM ten Thije Boonkkamp, ​​J van Dijk, L Liu, Расширение полной схемы потоков на системы законов сохранения, J Sci Comput (2012) 53: 552–568, DOI 10.1007 / s10915-012-9588-5
5. Вайсштейн, Эрик В. "Функция Coshc". Материал из MathWorld - веб-ресурса Wolfram. http://mathworld.wolfram.com/CoshcFunction.html^{[постоянная мертвая ссылка ]}