Закон Дарси - Darcys law - Wikipedia

Закон Дарси - уравнение, описывающее течение жидкость через пористый средний. Закон был сформулирован Генри Дарси по результатам экспериментов^[1] на потоке воды через кровати песок, составляющие основу гидрогеология, филиал науки о Земле.

Фон

Закон Дарси был впервые экспериментально определен Дарси, но с тех пор он был выведен из Уравнения Навье – Стокса через гомогенизация методы.^[2] Это аналог Закон Фурье в области теплопроводность, Закон Ома в области электрические сети, и Закон Фика в распространение теория.

Одно из применений закона Дарси - анализ потока воды через водоносный горизонт; Закон Дарси вместе с уравнением сохранение массы упрощается до уравнение потока грунтовых вод, одно из основных соотношений гидрогеология.

Моррис Маскат первый^{[нужна цитата ]} уточнил уравнение Дарси для однофазного потока, включив вязкость в уравнение Дарси для однофазной (жидкой) фазы. Это изменение сделало его пригодным для исследователей в нефтяной промышленности. Основываясь на экспериментальных результатах его коллег Вайкоффа и Ботсета, Маскат и Мерес также обобщили закон Дарси, чтобы охватить многофазный поток воды, нефти и газа в пористой среде нефтяного коллектора. Обобщенные уравнения многофазного потока, разработанные Маскатом и другими, обеспечивают аналитическую основу для разработки месторождений, которая существует по сей день.

Описание

Диаграмма, показывающая определения и направления закона Дарси. A - площадь поперечного сечения (м²) цилиндра. Q - расход (м³/ с) жидкости, протекающей через область A. Поток жидкости через A равен q = Q / A. L - длина цилиндра. Δp = p_{торговая точка} - п_вход = p_б - п_а. ${\displaystyle \nabla p}$ = Δp / L = гидравлический градиент, приложенный между точками a и b.

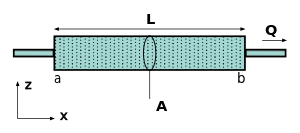
Закон Дарси, уточненный Моррис Маскат, в отсутствие гравитационные силы и в однородно проницаемой среде определяется простым соотношением пропорциональности между мгновенными поток ${\displaystyle q}$ (q = Q / A, единица: (м³ жидкости / с) / м²) через пористая среда, то проницаемость ${\displaystyle k}$ среды, динамический вязкость жидкости ${\displaystyle \mu }$, а падение давления ${\displaystyle \nabla p}$ на заданном расстоянии в виде^[3]

${\displaystyle q=-{\frac {k}{\mu }}\nabla p\,.}$

Это уравнение для однофазного (жидкого) потока представляет собой определяющее уравнение^[4] за абсолютная проницаемость (однофазная проницаемость).

Что касается диаграммы справа, поток ${\displaystyle q}$, или расход на единицу площади, определяется в единицах ${\displaystyle (m/s)}$, проницаемость ${\displaystyle k}$ в единицах ${\displaystyle (m^{2})}$, площадь поперечного сечения ${\displaystyle A}$ в единицах ${\displaystyle (m^{2})}$, полное падение давления ${\displaystyle \Delta p=p_{b}-p_{a}}$ в единицах ${\displaystyle (Pa)}$, то динамическая вязкость ${\displaystyle \mu }$ в единицах ${\displaystyle (Pa\cdot s)}$, и ${\displaystyle L}$ длина выборки в единицах ${\displaystyle (m)}$. Некоторые из этих параметров используются в альтернативных определениях ниже. Отрицательный знак используется в определении потока в соответствии со стандартным физическим соглашением, согласно которому жидкости текут из областей высокого давления в области низкого давления. Обратите внимание, что высота головы необходимо учитывать, если вход и выход находятся на разной высоте. Если изменение давления отрицательное, то расход будет положительным. Икс направление. Было несколько предложений по конститутивное уравнение для абсолютной проницаемости, и самый известный из них, вероятно, Уравнение Козени (также называемый Уравнение Козени – Кармана ).

Интегральная форма закона Дарси дается:

${\displaystyle Q={\frac {kA}{\mu L}}\,{\Delta p}\,}$

куда Q (единицы объема за время, например, м³/ s) - это полная разрядка. Рассматривая соотношение для статического давления жидкости (Закон стевина ):

${\displaystyle p=\rho gh}$

можно вывести представление

${\displaystyle Q={\frac {kAg}{\nu L}}\,{\Delta h}\,}$

где ν - кинематическая вязкость Соответствующие гидравлическая проводимость следовательно является:

${\displaystyle K={\frac {\nu L}{kAg}}}$

Это количество ${\displaystyle K}$, часто называемая потоком Дарси или скоростью Дарси, не является скоростью, с которой жидкость движется через поры. В скорость потока (ты) связана с потоком (q) посредством пористость (φ) и принимает вид

${\displaystyle u={\frac {q}{\varphi }}\,.}$

Закон Дарси - это простое математическое утверждение, которое аккуратно суммирует несколько знакомых свойств, которые грунтовые воды течет в водоносные горизонты экспонаты, в том числе:

• если на расстоянии нет градиента давления, поток не возникает (это гидростатический условия),
• если есть градиент давления, поток будет происходить от высокого давления к низкому давлению (противоположно направлению возрастающего градиента - отсюда отрицательный знак в законе Дарси),
• чем больше градиент давления (через тот же материал пласта), тем больше скорость разряда, и
• скорость истечения жидкости часто будет разной - через разные материалы пласта (или даже через тот же материал, в другом направлении) - даже если в обоих случаях существует одинаковый градиент давления.

Графическая иллюстрация использования установившегося режима уравнение потока грунтовых вод (на основе закона Дарси и сохранения массы) заключается в построении сети, чтобы количественно оценить количество грунтовые воды течет под плотина.

Закон Дарси действует только для медленных, вязкий поток; однако в эту категорию попадает большинство случаев стока подземных вод. Обычно любой поток с Число Рейнольдса меньше единицы явно ламинарный, и было бы справедливо применить закон Дарси. Экспериментальные испытания показали, что режимы течения с числами Рейнольдса до 10 все еще могут быть дарсианскими, как и в случае потока грунтовых вод. Число Рейнольдса (безразмерный параметр) для потока в пористой среде обычно выражается как

${\displaystyle \mathrm {Re} ={\frac {ud}{\nu }}\,,}$

куда ν это кинематическая вязкость из воды, ты - удельный расход (а не скорость поры - в единицах длины за время), d₃₀ представляет собой типичный диаметр зерна для пористой среды (стандартный выбор - d30, что составляет 30% проходящего размера от размером с зернышко анализ с помощью сит - с единицами длины).

Вывод

Для стационарного, ползучего несжимаемого потока, т.е. D(ρu_я)/Dt ≈ 0, уравнение Навье – Стокса упрощается до Уравнение Стокса, который без учета массового члена равен:

${\displaystyle \mu \nabla ^{2}u_{i}-\partial _{i}p=0\,,}$

куда μ вязкость, ты_я - скорость в я направление, грамм_я - гравитационная составляющая в я направление и п это давление. Предполагая, что сила вязкого сопротивления линейна со скоростью, мы можем написать:

${\displaystyle -\left(k_{ij}\right)^{-1}\mu \varphi u_{j}-\partial _{i}p=0\,,}$

куда φ это пористость, и k_ij - тензор проницаемости второго порядка. Это дает скорость в п направление,

${\displaystyle k_{ni}\left(k_{ij}\right)^{-1}u_{j}=\delta _{nj}u_{j}=u_{n}=-{\frac {k_{ni}}{\varphi \mu }}\partial _{i}p\,,}$

что дает закон Дарси для объемной плотности потока в п направление,

${\displaystyle q_{n}=-{\frac {k_{ni}}{\mu }}\,\partial _{i}p\,.}$

В изотропный пористая среда недиагональные элементы в тензоре проницаемости равны нулю, k_ij = 0 за я ≠ j и диагональные элементы идентичны, k_ii = k, и общий вид получается

${\displaystyle {\boldsymbol {q}}=-{\frac {k}{\mu }}\,{\boldsymbol {\nabla }}p\,.}$

Вышеприведенное уравнение представляет собой управляющее уравнение для однофазного течения жидкости в пористой среде.

Использование в нефтяной инженерии

Другой вывод закона Дарси широко используется в нефтяная инженерия для определения потока через проницаемую среду - самый простой из них для одномерного, однородного горного пласта с единственной жидкой фазой и постоянной жидкостью вязкость.

Почти все нефтяные пласты имеют водную зону под нефтяной ветвью, а некоторые также имеют газовую шапку над нефтяной веткой. Когда пластовое давление падает из-за добычи нефти, вода поступает в нефтяную зону снизу, а газ течет в нефтяную зону сверху (если существует газовая шапка), и мы получаем одновременный поток и несмешивающееся перемешивание всех фаз флюида в нефтяная зона. Оператор нефтяного месторождения может также закачивать воду (и / или газ), чтобы улучшить добычу нефти. Поэтому в нефтяной промышленности используется обобщенное уравнение Дарси для многофазного потока, которое было разработано Мускат и др. Поскольку имя Дарси так широко распространено и тесно связано с течением в пористой среде, многофазное уравнение обозначается Закон Дарси для многофазного потока или обобщенное уравнение (или закон) Дарси, или просто уравнение (или закон) Дарси, или просто уравнение потока, если в контексте говорится, что в тексте обсуждается многофазное уравнение Мускат и др. Многофазный поток в нефтяных и газовых коллекторах - обширная тема, и одна из многих статей по этой теме - Закон Дарси для многофазного потока.

Дополнительные формы

Квадратичный закон

Для течений в пористых средах с Числа Рейнольдса больше чем примерно от 1 до 10, инерционный эффекты также могут стать значительными. Иногда инерционный член добавляется к уравнению Дарси, известному как Форххаймер срок. Этот термин может объяснить нелинейный поведение разницы давлений в зависимости от данных расхода.^[5]

${\displaystyle {\frac {\partial p}{\partial x}}=-{\frac {\mu }{k}}q-{\frac {\rho }{k_{1}}}q^{2}\,,}$

где дополнительный член k₁ называется инерционной проницаемостью.

Течение в середине коллектора из песчаника настолько медленное, что уравнение Форххаймера обычно не требуется, но поток газа в газодобывающую скважину может быть достаточно высоким, чтобы оправдать использование уравнения Форхгеймера. В этом случае расчеты притока для скважины, а не для ячейки сетки 3D-модели, основаны на уравнении Форхгеймера. Эффект этого заключается в том, что в формуле характеристик притока появляется дополнительный зависящий от скорости скин-фактор.

Некоторые карбонатные коллекторы имеют много трещин, и уравнение Дарси для многофазного потока обобщено, чтобы управлять как потоком в трещинах, так и потоком в матрице (то есть традиционной пористой породе). Неровная поверхность стенок трещин и высокая скорость потока в трещинах могут оправдать использование уравнения Форхгеймера.

Поправка на газы в мелкодисперсных средах (диффузия Кнудсена или эффект Клинкенберга)

Для газового потока с небольшими характеристическими размерами (например, очень мелкий песок, нанопористые структуры и т. Д.) Взаимодействия частицы со стенкой становятся более частыми, что приводит к дополнительному трению стенки (трение Кнудсена). Для потока в этой области, где оба вязкий и Knudsen трение присутствует, необходимо использовать новую рецептуру. Knudsen представил полуэмпирическую модель течения в переходном режиме, основанную на его экспериментах с небольшими капиллярами.^[6][7] Для пористой среды уравнение Кнудсена можно записать в виде^[7]

${\displaystyle N=-\left({\frac {k}{\mu }}{\frac {p_{a}+p_{b}}{2}}+D_{\mathrm {K} }^{\mathrm {eff} }\right){\frac {1}{R_{\mathrm {g} }T}}{\frac {p_{\mathrm {b} }-p_{\mathrm {a} }}{L}}\,,}$

куда N молярный поток, р_грамм - газовая постоянная, Т это температура, D^эфф
_K - эффективный коэффициент диффузии Кнудсена пористой среды. Модель также может быть получена из основанной на первых принципах бинарной модели трения (BFM).^[8][9] Дифференциальное уравнение переходного течения в пористой среде на основе BFM имеет вид^[8]

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}N\,.}$

Это уравнение справедливо для капилляры а также пористые среды. Терминология эффекта Кнудсена и коэффициента диффузии Кнудсена более распространена в механический и химическая инженерия. В геологической и нефтехимической инженерии этот эффект известен как Эффект Клинкенберга. Используя определение молярного потока, приведенное выше уравнение можно переписать как

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}{\dfrac {p}{R_{\mathrm {g} }T}}q\,.}$

Это уравнение можно преобразовать в следующее уравнение

${\displaystyle q=-{\frac {k}{\mu }}\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right){\frac {\partial p}{\partial x}}\,.}$

Сравнивая это уравнение с обычным законом Дарси, можно дать новую формулировку:

${\displaystyle q=-{\frac {k^{\mathrm {eff} }}{\mu }}{\frac {\partial p}{\partial x}}\,,}$

куда

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right)\,.}$

Это эквивалентно формулировке эффективной проницаемости, предложенной Клинкенбергом:^[10]

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {b}{p}}\right)\,.}$

куда б известен как параметр Клинкенберга, который зависит от газа и структуры пористой среды. Это совершенно очевидно, если сравнить приведенные выше формулировки. Параметр Клинкенберга б зависит от проницаемости, коэффициента диффузии Кнудсена и вязкости (т. е. свойств газа и пористой среды).

Закон Дарси для коротких временных масштабов

Для очень коротких временных масштабов к закону Дарси может быть добавлена ​​производная потока по времени, что приведет к действительным решениям в очень короткие промежутки времени (в теплопередаче это называется модифицированной формой Закон Фурье ),

${\displaystyle \tau {\frac {\partial q}{\partial t}}+q=-k\nabla h\,,}$

куда τ - очень малая постоянная времени, которая приводит к приведению этого уравнения к нормальной форме закона Дарси в "нормальные" моменты времени (> наносекунды ). Основная причина этого заключается в том, что обычный уравнение потока грунтовых вод (уравнение диффузии ) приводит к особенности при постоянных границах напора при очень малых временах. Эта форма математически более строгая, но приводит к гиперболический уравнение потока грунтовых вод, которое сложнее решить и полезно только в очень короткие промежутки времени, как правило, за пределами практического использования.

Форма Бринкмана закона Дарси

Еще одно расширение традиционной формы закона Дарси - это термин Бринкмана, который используется для учета переходного потока между границами (введенный Бринкманом в 1949 г.^[11]),

${\displaystyle -\beta \nabla ^{2}q+q=-{\frac {k}{\mu }}\nabla p\,,}$

куда β эффективный вязкость срок. Этот поправочный член учитывает поток через среду, где зерна среды сами по себе являются пористыми, но их трудно использовать, и им обычно пренебрегают. Например, если пористый внеклеточный матрикс разрушается, образуя большие поры по всей матрице, термин вязкости применяется к большим порам, а закон Дарси применяется к оставшейся неповрежденной области. Этот сценарий был рассмотрен в теоретическом и модельном исследовании.^[12] В предлагаемой модели уравнение Бринкмана связано с набором уравнения реакции-диффузии-конвекции.

Действительность закона Дарси

Закон Дарси действует для ламинарный поток через отложения. В мелкозернистых отложениях размеры пустоты малы и поэтому поток ламинарный. Крупнозернистые отложения также ведут себя аналогичным образом, но в очень крупнозернистых отложениях поток может быть бурный.^[13] Следовательно, закон Дарси не всегда справедлив в таких отложениях. Для потока через промышленные круглые трубы поток является ламинарным, когда число Рейнольдса меньше 2000, и турбулентным, когда оно больше 4000, но в некоторых отложениях было обнаружено, что поток является ламинарным когда значение числа Рейнольдса меньше 1.^[14]

Смотрите также

• В Дарси, единица проницаемости для жидкости
• Гидрогеология
• Уравнение потока грунтовых вод
• Математическая модель
• Уравнения черной нефти

Рекомендации

1. Дарси, Х. (1856 г.). Публичные фонты виль-де-Дижон. Париж: Дальмон.
2. Уитакер, С. (1986). «Течение в пористой среде I: теоретический вывод закона Дарси». Транспорт в пористой среде. 1: 3–25. Дои:10.1007 / BF01036523.
3. Масуди, Реза; Пиллаи, Кришна М; Grahl, Ник; Тан, Хуа (13 февраля 2012 г.). «Численное моделирование заливки формы LCM при производстве композитов из натурального волокна». Журнал армированных пластиков и композитов. 31 (6): 363–378. Bibcode:2012JRPC ... 31..363M. Дои:10.1177/0731684412438629. ISSN  0731-6844.
4. Заранди, М. Амин Ф .; Пиллаи, Кришна М .; Киммел, Адам С. (2018). «Самопроизвольное впитывание жидкости в фитили из стекловолокна. Часть I: Полезность подхода с острым фронтом». Журнал Айше. 64: 294–305. Дои:10.1002 / aic.15965.
5. Бежан, А. (1984). Конвекционная теплопередача. Джон Вили и сыновья.
6. Cunningham, R.E .; Уильямс, Р. Дж. Дж. (1980). Диффузия в газах и пористых средах. Нью-Йорк: Пленум Пресс.
7. Carrigy, N .; Pant, L.M .; Mitra, S.K .; Секанелл, М. (2013). «Коэффициент диффузии Кнудсена и проницаемость газодиффузионных слоев с микропористым покрытием из ПМФК для различных нагрузок политетрафторэтилена». Журнал Электрохимического общества. 160 (2): F81–89. Дои:10.1149 / 2.036302jes.
8. Pant, L.M .; Mitra, S.K .; Секанелл, М. (2012). «Измерения абсолютной проницаемости и коэффициента диффузии Кнудсена в газодиффузионных слоях PEMFC и микропористых слоях». Журнал источников энергии. 206: 153–160. Дои:10.1016 / j.jpowsour.2012.01.099.
9. Керхоф, П. (1996). «Модифицированная модель Максвелла – Стефана для переноса через инертные мембраны: бинарная модель трения». Журнал химической инженерии и журнал биохимической инженерии. 64 (3): 319–343. Дои:10.1016 / S0923-0467 (96) 03134-X.
10. Клинкенберг, Л. Дж. (1941). «Проницаемость пористых сред для жидкостей и газов». Практика бурения и добычи. Американский нефтяной институт. С. 200–213.
11. Бринкман, Х.С. (1949). «Расчет вязкой силы, оказываемой текущей жидкостью на плотный рой частиц». Прикладные научные исследования. 1: 27–34. CiteSeerX  10.1.1.454.3769. Дои:10.1007 / BF02120313.
12. Wertheim, Kenneth Y .; Русе, Тийна (апрель 2017 г.). «Математическая модель лимфангиогенеза в эмбрионе рыбок данио». Вестник математической биологии. 79 (4): 693–737. Дои:10.1007 / s11538-017-0248-7. ISSN  1522-9602. ЧВК  5501200. PMID  28233173.
13. Jin, Y .; Ут, М.-Ф .; Кузнецов, А. В .; Хервиг, Х. (2 февраля 2015 г.). «Численное исследование возможности макроскопической турбулентности в пористых средах: исследование методом прямого численного моделирования». Журнал гидромеханики. 766: 76–103. Bibcode:2015JFM ... 766 ... 76J. Дои:10.1017 / jfm.2015.9.
14. Арора, К. Р. (1989). Механика грунтов и фундаментостроение. Стандартные издатели.