Уравнение Экхауза - Eckhaus equation - Wikipedia

В математическая физика, то Уравнение Экхауза - или Уравнение Кунду – Экхауза - нелинейный уравнения в частных производных в пределах нелинейный Шредингер учебный класс:^[1]

${\displaystyle i\psi _{t}+\psi _{xx}+2\left(|\psi |^{2}\right)_{x}\,\psi +|\psi |^{4}\,\psi =0.}$

Уравнение было независимо введено Виктор Экхаус и Анжан Кунду для моделирования распространения волны в дисперсионные среды.^[2][3]

Линеаризация

Анимация волновой пакет решение уравнения Экхауза. Синяя линия - это реальная часть решения, красная линия - это мнимая часть а черная линия - это огибающая волны (абсолютная величина ). Обратите внимание асимметрия в конверте ${\displaystyle |\psi (x,t)|}$ для уравнения Экхауза, а огибающая ${\displaystyle |\varphi (x,t)|}$ - соответствующего решения линейного уравнения Шредингера - симметрично (в ${\displaystyle x}$). Короткие волны в пакете распространяются быстрее, чем длинные.

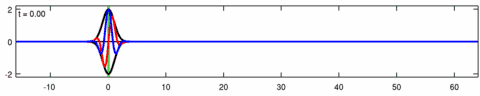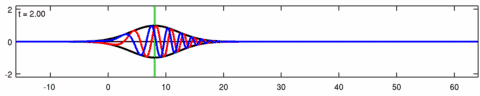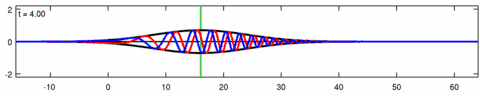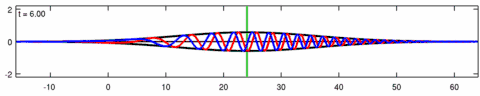
Анимация волновой пакет решение линейное уравнение Шредингера - соответствует приведенной выше анимации для уравнения Экхауза. Синяя линия - это реальная часть решения, красная линия - это мнимая часть, черная линия - это огибающая волны (абсолютная величина ), а зеленая линия - это центроид огибающей волнового пакета.

Уравнение Экхауза может быть линеаризованный к линейное уравнение Шредингера:^[4]

${\displaystyle i\varphi _{t}+\varphi _{xx}=0,}$

через нелинейное преобразование:^[5]

${\displaystyle \varphi (x,t)=\psi (x,t)\,\exp \left(\int _{-\infty }^{x}|\psi (x^{\prime },t)|^{2}\;{\text{d}}x^{\prime }\right).}$

Обратное преобразование:

${\displaystyle \psi (x,t)={\frac {\varphi (x,t)}{\displaystyle \left(1+2\,\int _{-\infty }^{x}|\varphi (x^{\prime },t)|^{2}\;{\text{d}}x^{\prime }\right)^{1/2}}}.}$

Эта линеаризация также означает, что уравнение Экхауза имеет вид интегрируемый.

Примечания

1. Цвиллинджер (1998, стр. 177 и 390).
2. Экхаус (1985)
3. Кунду (1984)
4. Калоджеро и Де Лилло (1987)
5. Абловиц, Аренс и Де Лилло (2005)

Рекомендации

• Абловиц, М.Дж.; Ahrens, C.D .; Де Лилло, С. (2005), "О" квази "интегрируемом дискретном уравнении Экхауза", Журнал нелинейной математической физики, 12 (Приложение 1): 1–12, Bibcode:2005JNMP ... 12S ... 1A, Дои:10.2991 / jnmp.2005.12.s1.1
• Калоджеро, Ф.; Де Лилло, С. (1987), "Eckhaus PDE" яψ_т + ψ_хх+ 2 (| ψ |²)_Икс ψ + | ψ |⁴ ψ = 0 ", Обратные задачи, 3 (4): 633–682, Bibcode:1987InvPr ... 3..633C, Дои:10.1088/0266-5611/3/4/012
• Экхаус, В. (1985), Долговременное поведение для возмущенных волновых уравнений и связанных задач, Департамент математики, Утрехтский университет, Препринт № 404.
  Частично опубликовано в: Eckhaus, W. (1986), "Долговременное поведение для возмущенных волновых уравнений и родственные проблемы", в Kröner, E .; Кирхгесснер, К. (ред.), Тенденции в приложениях чистой математики к механике, Конспект лекций по физике, 249, Берлин: Springer, стр. 168–194, Дои:10.1007 / BFb0016391, ISBN  978-3-540-16467-8
• Кунду, А. (1984), "Калибровка нелинейных систем Ландау – Лифшица и высших порядков, порожденных нелинейными уравнениями типа Шредингера", Журнал математической физики, 25: 3433–3438, Bibcode:1984JMP .... 25,3433K, Дои:10.1063/1.526113
• Taghizadeh, N .; Мирзазаде, М .; Таскан, Ф. (2012), "Метод первого интеграла, примененный к уравнению Экхауза", Письма по прикладной математике, 25 (5): 798–802, Дои:10.1016 / j.aml.2011.10.021
• Цвиллинджер, Д. (1998), Справочник по дифференциальным уравнениям (3-е изд.), Academic Press, ISBN  978 0 12 784396 4