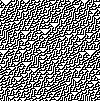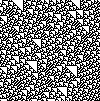Элементарный клеточный автомат - Elementary cellular automaton

В математика и теория вычислимости, элементарный клеточный автомат является одномерным клеточный автомат где есть два возможных состояния (помечены 0 и 1), а правило определения состояния ячейки в следующем поколении зависит только от текущего состояния ячейки и двух ее ближайших соседей. Есть простейший клеточный автомат (Правило 110, определенный ниже), который способен универсальное вычисление, и как таковая это одна из простейших возможных моделей вычислений.

Система нумерации

Есть 8 = 2³ возможные конфигурации для ячейки и двух ее ближайших соседей. Правило, определяющее клеточный автомат, должно указывать результирующее состояние для каждой из этих возможностей, так что 256 = 2²³ возможные элементарные клеточные автоматы. Стивен Вольфрам предложил схему, известную как Код Wolfram, чтобы присвоить каждому правилу номер от 0 до 255, который стал стандартом. Каждая возможная текущая конфигурация записывается в порядке 111, 110, ..., 001, 000, и результирующее состояние для каждой из этих конфигураций записывается в том же порядке и интерпретируется как двоичное представление целого числа. Это число принято за номер правила автомата. Например, 110_d=01101110₂. Итак, правило 110 определяется правилом перехода:

111	110	101	100	011	010	001	000	текущий образец	P = (L, C, R)
0	1	1	0	1	1	1	0	новое состояние для центральной ячейки	N110d= (C + R + C * R + L * C * R)% 2

Размышления и дополнения

Хотя существует 256 возможных правил, многие из них тривиально эквивалентны друг другу вплоть до простого преобразования базовой геометрии. Первое такое преобразование - это отражение через вертикальную ось, и результат применения этого преобразования к заданному правилу называется зеркальное правило. Эти правила будут демонстрировать такое же поведение вплоть до отражения через вертикальную ось, и поэтому эквивалентны в вычислительном смысле.

Например, если определение правила 110 отображается вертикальной линией, получается следующее правило (правило 124):

111	110	101	100	011	010	001	000	текущий образец	P = (L, C, R)
0	1	1	1	1	1	0	0	новое состояние для центральной ячейки	N112d+12d=124d= (L + C + L * C + L * C * R)% 2

Правила, которые совпадают с их зеркальным правилом, называются амфихиральный. Из 256 элементарных клеточных автоматов 64 амфихиральны.

Второе такое преобразование - это поменять местами 0 и 1 в определении. Результат применения этого преобразования к данному правилу называется дополнительное правилоНапример, если это преобразование применяется к правилу 110, мы получаем следующее правило

текущий образец	000	001	010	011	100	101	110	111
новое состояние для центральной ячейки	1	0	0	1	0	0	0	1

и после изменения порядка мы обнаруживаем, что это правило 137:

текущий образец	111	110	101	100	011	010	001	000
новое состояние для центральной ячейки	1	0	0	0	1	0	0	1

Есть 16 правил, которые аналогичны своим дополнительным правилам.

Наконец, два предыдущих преобразования могут быть последовательно применены к правилу для получения зеркально отраженного дополнительного правила. Например, зеркальным дополнительным правилом правила 110 является правило 193. Существует 16 правил, которые аналогичны своим зеркальным дополнительным правилам.

Из 256 элементарных клеточных автоматов 88 неэквивалентны относительно этих преобразований.

Одиночные 1 истории

Один из методов, используемых для изучения этих автоматов, состоит в том, чтобы проследить его историю с начальным состоянием всех нулей, кроме одной ячейки с 1. Когда номер правила четный (так что вход 000 не приводит к 1), он делает смысл интерпретировать состояние каждый раз, т, как целое число, выраженное в двоичном формате, что дает последовательность а(т) целых чисел. Во многих случаях эти последовательности имеют простые выражения в замкнутой форме или имеют производящая функция с простой формой. Следует отметить следующие правила:

Правило 28

Сгенерированная последовательность: 1, 3, 5, 11, 21, 43, 85, 171, ... (последовательность A001045 в OEIS ). Это последовательность Числа Якобсталя и имеет производящую функцию

${displaystyle {frac {1+2x}{(1+x)(1-2x)}}}$.

Имеет выражение в закрытой форме

${displaystyle a(t)={frac {4cdot 2^{t}-(-1)^{t}}{3}}}$

Правило 156 генерирует ту же последовательность.

Правило 50

Сгенерированная последовательность: 1, 5, 21, 85, 341, 1365, 5461, 21845, ... (последовательность A002450 в OEIS ). Это имеет производящую функцию

${displaystyle {frac {1}{(1-x)(1-4x)}}}$.

Имеет выражение в закрытой форме

${displaystyle a(t)={frac {4cdot 4^{t}-1}{3}}}$.

Обратите внимание, что правила 58, 114, 122, 178, 186, 242 и 250 генерируют одну и ту же последовательность.

Правило 54

Сгенерированная последовательность: 1, 7, 17, 119, 273, 1911, 4369, 30583, ... (последовательность A118108 в OEIS ). Это производящая функция

${displaystyle {frac {1+7x}{(1-x^{2})(1-16x^{2})}}}$.

Имеет выражение в закрытой форме

${displaystyle a(t)={frac {22cdot 4^{t}-6(-4)^{t}-4+3(-1)^{t}}{15}}}$.

Правило 60

Сгенерированная последовательность: 1, 3, 5, 15, 17, 51, 85, 255, ... (последовательность A001317 в OEIS ). Этого можно добиться, взяв последовательные ряды Треугольник Паскаля по модулю 2 и интерпретируя их как целые числа в двоичной системе, которые могут быть графически представлены Треугольник Серпинского.

Правило 90

Основная статья: Правило 90

Сгенерированная последовательность: 1, 5, 17, 85, 257, 1285, 4369, 21845, ... (последовательность A038183 в OEIS ). Этого можно добиться, взяв последовательные ряды Треугольник Паскаля по модулю 2 и интерпретируя их как целые числа с основанием 4. Обратите внимание, что правила 18, 26, 82, 146, 154, 210 и 218 генерируют ту же последовательность.

Правило 94

Сгенерированная последовательность: 1, 7, 27, 119, 427, 1879, 6827, 30039, ... (последовательность A118101 в OEIS ). Это можно выразить как

${displaystyle a(t)={egin{cases}1,&{mbox{if }}t=0[5px]7,&{mbox{if }}t=1[7px]{dfrac {1+5cdot 4^{n}}{3}},&{mbox{if }}t{mbox{ is even otherwise}}[7px]{dfrac {10+11cdot 4^{n}}{6}},&{mbox{if }}t{mbox{ is odd otherwise}}end{cases}}}$.

Это производящая функция

${displaystyle {frac {(1+2x)(1+5x-16x^{4})}{(1-x^{2})(1-16x^{2})}}}$.

Правило 102

Сгенерированная последовательность: 1, 6, 20, 120, 272, 1632, 5440, 32640, ... (последовательность A117998 в OEIS ). Это просто последовательность, сгенерированная правилом 60 (которое является его правилом зеркала), умноженная на последовательные степени двойки.

Правило 110

Основная статья: Правило 110

Правило 150

Сгенерированная последовательность: 1, 7, 21, 107, 273, 1911, 5189, 28123, ... (последовательность A038184 в OEIS ). Этого можно добиться, взяв коэффициенты при последовательных степенях (1+Икс+Икс²) по модулю 2 и интерпретируя их как целые числа в двоичном формате.

Правило 158

Сгенерированная последовательность: 1, 7, 29, 115, 477, 1843, 7645, 29491, ... (последовательность A118171 в OEIS ). Это производящая функция

${displaystyle {frac {1+7x+12x^{2}-4x^{3}}{(1-x^{2})(1-16x^{2})}}}$.

Правило 188

Сгенерированная последовательность: 1, 3, 5, 15, 29, 55, 93, 247, ... (последовательность A118173 в OEIS ). Это имеет производящую функцию

${displaystyle {frac {1+3x+4x^{2}+12x^{3}+8x^{4}-8x^{5}}{(1-x^{2})(1-16x^{4})}}}$.

Правило 190

Сгенерированная последовательность: 1, 7, 29, 119, 477, 1911, 7645, 30583, ... (последовательность A037576 в OEIS ). Это производящая функция

${displaystyle {frac {1+3x}{(1-x^{2})(1-4x)}}}$.

Правило 220

Сгенерированная последовательность: 1, 3, 7, 15, 31, 63, 127, 255, ... (последовательность A000225 в OEIS ). Это последовательность Числа Мерсенна и имеет производящую функцию

${displaystyle {frac {1}{(1-x)(1-2x)}}}$.

Имеет выражение в закрытой форме

${displaystyle a(t)=2cdot 2^{t}-1}$.

Обратите внимание, что правило 252 генерирует ту же последовательность.

Правило 222

Сгенерированная последовательность: 1, 7, 31, 127, 511, 2047, 8191, 32767, ... (последовательность A083420 в OEIS ). Это каждая вторая запись в последовательности Числа Мерсенна и имеет производящую функцию

${displaystyle {frac {1+2x}{(1-x)(1-4x)}}}$.

Имеет выражение в закрытой форме

${displaystyle a(t)=2cdot 4^{t}-1}$.

Обратите внимание, что правило 254 генерирует ту же последовательность.

Случайное начальное состояние

Второй способ исследовать поведение этих автоматов - изучить их историю, начиная со случайного состояния. Это поведение можно лучше понять с точки зрения классов Wolfram. Вольфрам приводит следующие примеры в качестве типичных правил каждого класса.^[1]

• Класс 1: клеточные автоматы, которые быстро сходятся к однородному состоянию. Примерами являются правила 0, 32, 160 и 232.
• Класс 2: клеточные автоматы, которые быстро переходят в повторяющееся или стабильное состояние. Примерами являются правила 4, 108, 218 и 250.
• Класс 3: Клеточные автоматы, которые остаются в случайном состоянии. Примерами являются правила 22, 30, 126, 150, 182.
• Класс 4: клеточные автоматы, которые образуют области повторяющихся или стабильных состояний, но также образуют структуры, которые взаимодействуют друг с другом сложным образом. Примером является Правило 110. Было показано, что правило 110 способно универсальное вычисление.^[2]

Каждый вычисленный результат помещается в источник этих результатов, создавая двумерное представление эволюции системы. Следующие 88 неэквивалентных правил основаны на случайных начальных условиях:

• 

  Правило 0

• 

  Правило 1

• 

  Правило 2

• 

  Правило 3

• 

  Правило 4

• 

  Правило 5

• 

  Правило 6

• 

  Правило 7

• 

  Правило 8

• 

  Правило 9

• 

  Правило 10

• 

  Правило 11

• 

  Правило 12

• 

  Правило 13

• 

  Правило 14

• 

  Правило 15

• 

  Правило 18

• 

  Правило 19

• 

  Правило 22

• 

  Правило 23

• 

  Правило 24

• 

  Правило 25

• 

  Правило 26

• 

  Правило 27

• 

  Правило 28

• 

  Правило 29

• 

  Правило 30

• 

  Правило 32

• 

  Правило 33

• 

  Правило 34

• 

  Правило 35

• 

  Правило 36

• 

  Правило 37

• 

  Правило 38

• 

  Правило 40

• 

  Правило 41

• 

  Правило 42

• 

  Правило 43

• 

  Правило 44

• 

  Правило 45

• 

  Правило 46

• 

  Правило 50

• 

  Правило 51

• 

  Правило 54

• 

  Правило 56

• 

  Правило 57

• 

  Правило 58

• 

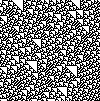
  Правило 60

• 

  Правило 62

• 

  Правило 72

• 

  Правило 73

• 

  Правило 74

• 

  Правило 76

• 

  Правило 77

• 

  Правило 78

• 

  Правило 90

• 

  Правило 94

• 

  Правило 104

• 

  Правило 105

• 

  Правило 106

• 

  Правило 108

• 

  Правило 110

• 

  Правило 122

• 

  Правило 126

• 

  Правило 128

• 

  Правило 130

• 

  Правило 132

• 

  Правило 134

• 

  Правило 136

• 

  Правило 138

• 

  Правило 140

• 

  Правило 142

• 

  Правило 146

• 

  Правило 150

• 

  Правило 152

• 

  Правило 154

• 

  Правило 156

• 

  Правило 160

• 

  Правило 162

• 

  Правило 164

• 

  Правило 168

• 

  Правило 170

• 

  Правило 172

• 

  Правило 178

• 

  Правило 184

• 

  Правило 200

• 

  Правило 204

• 

  Правило 232

Необычные случаи

В некоторых случаях поведение клеточного автомата не сразу очевидно. Например, для правила 62 взаимодействующие структуры развиваются как в классе 4. Но в этих взаимодействиях по крайней мере одна из структур уничтожается, поэтому автомат в конечном итоге переходит в повторяющееся состояние, а клеточный автомат относится к классу 2.^[3]

Правило 73 - это класс 2^[4] поскольку каждый раз, когда есть две последовательные единицы, окруженные нулями, эта функция сохраняется в последующих поколениях. Это эффективно создает стены, которые блокируют поток информации между различными частями массива. Существует конечное количество возможных конфигураций в секции между двумя стенами, поэтому автомат в конечном итоге должен начать повторяться внутри каждой секции, хотя период может быть очень длинным, если секция достаточно широкая. Эти стенки сформируются с вероятностью 1 при полностью случайных начальных условиях. Однако, если добавлено условие, что длины серий последовательных нулей или единиц всегда должны быть нечетными, то автомат будет отображать поведение класса 3, поскольку стены никогда не могут образоваться.

Правило 54 - это класс 4^[5] и также кажется способным к универсальным вычислениям, но не был изучен так тщательно, как Правило 110. Было каталогизировано много взаимодействующих структур, которые в совокупности, как ожидается, будут достаточными для универсальности.^[6]

Рекомендации

• Вайсштейн, Эрик В. «Элементарный клеточный автомат». MathWorld.
• Вайсштейн, Эрик В. «Правило 30». MathWorld.
• Вайсштейн, Эрик В. «Правило 50». MathWorld.
• Вайсштейн, Эрик В. «Правило 54». MathWorld.
• Вайсштейн, Эрик В. «Правило 60». MathWorld.
• Вайсштейн, Эрик В. «Правило 62». MathWorld.
• Вайсштейн, Эрик В. «Правило 90». MathWorld.
• Вайсштейн, Эрик В. «Правило 94». MathWorld.
• Вайсштейн, Эрик В. «Правило 102». MathWorld.
• Вайсштейн, Эрик В. «Правило 110». MathWorld.
• Вайсштейн, Эрик В. «Правило 126». MathWorld.
• Вайсштейн, Эрик В. «Правило 150». MathWorld.
• Вайсштейн, Эрик В. «Правило 158». MathWorld.
• Вайсштейн, Эрик В. «Правило 182». MathWorld.
• Вайсштейн, Эрик В. «Правило 188». MathWorld.
• Вайсштейн, Эрик В. «Правило 190». MathWorld.
• Вайсштейн, Эрик В. «Правило 220». MathWorld.
• Вайсштейн, Эрик В. «Правило 222». MathWorld.

1. Стивен Вольфрам, Новый вид науки p223 ff.
2. Правило 110 - Вольфрам | Альфа
3. Правило 62 - Вольфрам | Альфа
4. Правило 73 - Вольфрам | Альфа
5. Правило 54 - Вольфрам | Альфа
6. Мартенес, Хенаро Хуарес; Адамацкий, Андрей; Макинтош, Гарольд В. (01.04.2006). «Феноменология столкновений планеров в Правиле 54 клеточного автомата и связанных логических воротах» (PDF). Хаос, солитоны и фракталы. 28 (1): 100–111. Дои:10.1016 / j.chaos.2005.05.013. ISSN  0960-0779.

внешняя ссылка

• «Элементарные клеточные автоматы» на Вольфрам Атлас простых программ
• Отрисовка исполняемого файла MS-DOS длиной 32 байта клеточным автоматом (Правило 110 по умолчанию)
• Витрина всех правил, выбранных наугад
• Минимальная эмуляция CA с помощью парсера правил Wolfram онлайн на ванильном Javascript