Треугольник Паскаля - Pascals triangle - Wikipedia

${\displaystyle {\begin{array}{c}1\\1\quad 1\\1\quad 2\quad 1\\1\quad 3\quad 3\quad 1\\1\quad 4\quad 6\quad 4\quad 1\\1\quad 5\quad 10\quad 10\quad 5\quad 1\\1\quad 6\quad 15\quad 20\quad 15\quad 6\quad 1\\1\quad 7\quad 21\quad 35\quad 35\quad 21\quad 7\quad 1\\\end{array}}}$

Диаграмма, показывающая треугольник Паскаля со строками от 0 до 7.

В математика, Треугольник Паскаля это треугольная решетка из биномиальные коэффициенты что возникает в теории вероятностей, комбинаторике и алгебре. В большей части западный мир, назван в честь французского математика Блез Паскаль, хотя другие математики изучал его за столетия до него в Индии,^[1] Персия,^[2] Китай, Германия и Италия.^[3]

Строки треугольника Паскаля условно нумеруются, начиная с row п = 0 вверху (0-я строка). Записи в каждой строке нумеруются слева, начиная с k = 0 и обычно располагаются в шахматном порядке относительно чисел в соседних строках. Треугольник может быть построен следующим образом: В строке 0 (самая верхняя строка) есть уникальная ненулевая запись 1. Каждая запись каждой последующей строки создается путем добавления числа вверху и слева с номером вверху и к справа, обрабатывая пустые записи как 0. Например, начальное число в первой (или любой другой) строке равно 1 (сумма 0 и 1), тогда как числа 1 и 3 в третьей строке складываются для получения цифра 4 в четвертом ряду.

Формула

В треугольнике Паскаля каждое число представляет собой сумму двух чисел прямо над ним.

Запись в пй ряд и k-й столбец треугольника Паскаля обозначается ${\displaystyle {\tbinom {n}{k}}}$. Например, уникальная ненулевая запись в самой верхней строке ${\displaystyle {\tbinom {0}{0}}=1}$. С этими обозначениями конструкция предыдущего абзаца может быть записана следующим образом:

${\displaystyle {n \choose k}={n-1 \choose k-1}+{n-1 \choose k}}$,

для любого неотрицательного целого числа п и любое целое число k от 0 до п, включительно.^[4] Это повторение для биномиальных коэффициентов известно как Правило Паскаля.

У треугольника Паскаля выше размерный обобщения. Трехмерная версия называется Пирамида паскаля или же Тетраэдр Паскаля, а общие версии называются Симплексы Паскаля.

История

मेरु प्रस्तार (Меру Прастара), как используется в индийских рукописях, происходит от Пингала формулы. Рукопись из библиотеки Рагхунатха J&K; 755 г. н.э.

Ян Хуэй треугольник, изображенный китайцами с помощью стержневые цифры, появляется в математическая работа к Чжу Шицзе, датированный 1303 годом. Название гласит: «Схема семи квадратов умножения по старинному методу» (китайский язык: 古法 七 乘方 圖; четвертый символ 椉 в названии изображения архаичен).

Паскаль версия треугольника

Схема чисел, образующих треугольник Паскаля, была известна задолго до Паскаля. Паскаль ввел новшества во многие ранее неизвестные способы использования чисел треугольника, которые он подробно описал в самых ранних известных математических работах. научный труд быть специально посвященным треугольнику, его Арифметический треугольник (1654; опубликовано 1665). Несколько веков назад обсуждение чисел возникло в контексте Индийский исследования комбинаторика и биномиальных чисел и Греки ' исследование фигуральные числа.^[5]

Из более поздних комментариев видно, что биномиальные коэффициенты и аддитивная формула для их генерации, ${\displaystyle {\tbinom {n}{r}}={\tbinom {n-1}{r}}+{\tbinom {n-1}{r-1}}}$, были известны Пингала в или до 2-го века до нашей эры.^[6][7] Хотя работы Пингалы сохранились лишь фрагментарно, комментатор Варахамихира около 505 г., дал четкое описание аддитивной формулы,^[7] и более подробное объяснение того же правила было дано Халаюда, около 975. Халаюдха также объяснил неясные ссылки на Меру-прастара, то Лестница Гора Меру, давая первое сохранившееся описание расположения этих чисел в треугольник.^[7][8] Примерно в 850 г. Джайн математик Махавира дал другую формулу для биномиальных коэффициентов, используя умножение, эквивалентную современной формуле ${\displaystyle {\tbinom {n}{r}}={\tfrac {n!}{r!(n-r)!}}}$.^[7] В 1068 году математик дал четыре столбца первых шестнадцати строк. Бхаттотпала, который был первым зарегистрированным математиком, который приравнял аддитивные и мультипликативные формулы для этих чисел.^[7]

Примерно в то же время Персидский математик Аль-Караджи (953–1029) написал ныне утерянную книгу, содержащую первое описание треугольника Паскаля.^[9][10][11] Позже его повторил персидский поэт-астроном-математик. Омар Хайям (1048–1131); таким образом, треугольник также называют Треугольник Хайям в Иране.^[12] Было известно несколько теорем, связанных с треугольником, в том числе биномиальная теорема. Хайям использовал метод поиска пкорни на основе биномиального разложения и, следовательно, биномиальных коэффициентов.^[2]

Треугольник Паскаля был известен в Китае в начале 11 века благодаря работам китайского математика. Цзя Сянь (1010–1070). В 13 веке Ян Хуэй (1238–1298) представили треугольник, и поэтому его до сих пор называют Треугольник Ян Хуэя (杨辉 三角; 楊輝 三角) в Китае.^[13]

На западе треугольник Паскаля впервые появляется в арифметике Иорданус де Немор (13 век).^[14]Биномиальные коэффициенты рассчитывались по формуле Герсонид в начале 14 века, используя для них формулу умножения.^[7] Петрус Апианус (1495–1552) опубликовал полный треугольник на фронтиспис его книги по бизнес-расчетам в 1527 году.^[15] Майкл Стифель опубликовал часть треугольника (от второго до среднего столбца в каждой строке) в 1544 году, описав его как таблицу фигуральные числа.^[7] В Италии треугольник Паскаля называют Треугольник Тартальи, названный в честь итальянского алгебраиста Никколо Фонтана Тарталья (1500–1577), опубликовавший в 1556 году шесть рядов треугольника.^[7] Джероламо Кардано также опубликовал треугольник, а также аддитивные и мультипликативные правила его построения в 1570 году.^[7]

Паскаля Арифметический треугольник (Трактат об арифметическом треугольнике) был опубликован в 1655 году. В нем Паскаль собрал несколько известных на тот момент результатов о треугольнике и использовал их для решения задач в теория вероятности. Позднее треугольник был назван в честь Паскаля. Пьер Раймон де Монморт (1708), который назвал его «Table de M. Pascal pour les combinaisons» (французский язык: Таблица г-на Паскаля для комбинаций) и Авраам де Муавр (1730), который назвал его «Triangulum Arithmeticum PASCALIANUM» (лат.: Арифметический треугольник Паскаля), что стало современным западным названием.^[16]

Биномиальные разложения

Визуализация биномиального разложения до 4-й степени

Треугольник Паскаля определяет коэффициенты, которые возникают в биномиальные разложения. Например, рассмотрим расширение

(Икс + у)² = Икс² + 2ху + у² = 1Икс²у⁰ + 2Икс¹у¹ + 1Икс⁰у².

Коэффициенты - это числа во второй строке треугольника Паскаля: 1, 2, 1. В общем, когда биномиальный подобно Икс + у возводится в положительную целую степень, мы имеем:

(Икс + у)^п = а₀Икс^п + а₁Икс^п−1у + а₂Икс^п−2у² + ... + а_п−1ху^п−1 + а_пу^п,

где коэффициенты а_я в этом раскрытии - именно числа в строке п треугольника Паскаля. Другими словами,

${\displaystyle a_{i}={n \choose i}.}$

Это биномиальная теорема.

Вся правая диагональ треугольника Паскаля соответствует коэффициенту при у^п в этих биномиальных разложениях, а следующая диагональ соответствует коэффициенту при ху^п−1 и так далее.

Чтобы увидеть, как биномиальная теорема связана с простым построением треугольника Паскаля, рассмотрим задачу вычисления коэффициентов разложения (Икс + 1)^п+1 через соответствующие коэффициенты при (Икс + 1)^п (параметр у = 1 для простоты). Предположим тогда, что

${\displaystyle (x+1)^{n}=\sum _{i=0}^{n}a_{i}x^{i}.}$

Сейчас же

${\displaystyle (x+1)^{n+1}=(x+1)(x+1)^{n}=x(x+1)^{n}+(x+1)^{n}=\sum _{i=0}^{n}a_{i}x^{i+1}+\sum _{i=0}^{n}a_{i}x^{i}.}$

${\displaystyle {\begin{array}{c}{\binom {0}{0}}\\{\binom {1}{0}}\quad {\binom {1}{1}}\\{\binom {2}{0}}\quad {\binom {2}{1}}\quad {\binom {2}{2}}\\{\binom {3}{0}}\quad {\binom {3}{1}}\quad {\binom {3}{2}}\quad {\binom {3}{3}}\\{\binom {4}{0}}\quad {\binom {4}{1}}\quad {\binom {4}{2}}\quad {\binom {4}{3}}\quad {\binom {4}{4}}\\{\binom {5}{0}}\quad {\binom {5}{1}}\quad {\binom {5}{2}}\quad {\binom {5}{3}}\quad {\binom {5}{4}}\quad {\binom {5}{5}}\end{array}}}$

Шесть строк треугольника Паскаля как биномиальные коэффициенты

Два суммирования можно реорганизовать следующим образом:

${\displaystyle {\begin{aligned}\sum _{i=0}^{n}a_{i}x^{i+1}+\sum _{i=0}^{n}a_{i}x^{i}&=\sum _{i=1}^{n+1}a_{i-1}x^{i}+\sum _{i=0}^{n}a_{i}x^{i}\\[6pt]&{}=\sum _{i=1}^{n}a_{i-1}x^{i}+\sum _{i=1}^{n}a_{i}x^{i}+a_{0}x^{0}+a_{n}x^{n+1}\\[6pt]&{}=\sum _{i=1}^{n}(a_{i-1}+a_{i})x^{i}+a_{0}x^{0}+a_{n}x^{n+1}\\[6pt]&{}=\sum _{i=1}^{n}(a_{i-1}+a_{i})x^{i}+x^{0}+x^{n+1}\end{aligned}}}$

(из-за того, как работает возведение многочлена в степень, а₀ = а_п = 1).

Теперь у нас есть выражение для полинома (Икс + 1)^п+1 через коэффициенты при (Икс + 1)^п (эти а_яs), что нам нужно, если мы хотим выразить строку через строку над ней. Напомним, что все члены на диагонали, идущей из верхнего левого угла в нижний правый, соответствуют одной и той же степени Икс, и что a-члены являются коэффициентами многочлена (Икс + 1)^п, и мы определяем коэффициенты при (Икс + 1)^п+1. Теперь для любого я не 0 или п + 1, коэффициент Икс^я член в полиноме (Икс + 1)^п+1 равно а_я−1 + а_я. Это действительно простое правило построения треугольника Паскаля строка за строкой.

Этот аргумент несложно превратить в доказательство (к математическая индукция ) биномиальной теоремы. С(а + б)^п = б^п(а/б + 1)^п, коэффициенты идентичны в разложении общего случая.

Интересное следствие биномиальной теоремы получается, если положить обе переменные Икс и у равно единице. В этом случае мы знаем, что (1 + 1)^п = 2^п, и так

${\displaystyle {n \choose 0}+{n \choose 1}+\cdots +{n \choose n-1}+{n \choose n}=2^{n}.}$

Другими словами, сумма записей в п-я строка треугольника Паскаля - это п-й степени 2. Это эквивалентно утверждению, что количество подмножеств (мощность набор мощности ) из п-элементный набор есть ${\displaystyle 2^{n}}$, как можно увидеть, наблюдая, что количество подмножеств является суммой количества комбинаций каждой из возможных длин, которые варьируются от нуля до п.

Комбинации

Второе полезное применение треугольника Паскаля - вычисление комбинации. Например, количество комбинаций п вещи взяты k одновременно (называется n выбрать k ) можно найти по уравнению

${\displaystyle \mathbf {C} (n,k)=\mathbf {C} _{k}^{n}={_{n}C_{k}}={n \choose k}={\frac {n!}{k!(n-k)!}}.}$

Но это также формула для ячейки треугольника Паскаля. Вместо того, чтобы выполнять вычисления, можно просто найти соответствующую запись в треугольнике. Если у нас есть первая строка и первая запись в строке с номером 0, ответ будет расположен в записи k в ряд п. Например, предположим, что в баскетбольной команде 10 игроков, и она хочет знать, сколько способов выбрать 8. Ответ - запись 8 в строке 10, что составляет 45; то есть 10 выберите 8 - это 45.

Связь с биномиальным распределением и свертками

При делении на 2^п, то п-я строка треугольника Паскаля становится биномиальное распределение в симметричном случае, когда п = 1/2. Посредством Центральная предельная теорема, это распределение приближается к нормальное распределение в качестве п увеличивается. Это также можно увидеть, применив Формула Стирлинга факториалам, входящим в формулу для комбинаций.

Это связано с работой дискретных свертка двумя способами. Во-первых, полиномиальное умножение точно соответствует дискретной свертке, так что многократная свертка последовательности {..., 0, 0, 1, 1, 0, 0, ...} с самой собой соответствует взятию степеней 1 +Икс, а значит, и к порождению строк треугольника. Во-вторых, многократно свертывая функцию распределения для случайная переменная с собой соответствует вычислению функции распределения для суммы п независимые копии этой переменной; это как раз та ситуация, к которой применима центральная предельная теорема и, следовательно, приводит к нормальному распределению в пределе.

Паттерны и свойства

Треугольник Паскаля обладает множеством свойств и содержит множество шаблонов чисел.

Каждый кадр представляет собой строку в треугольнике Паскаля. Каждый столбец пикселей представляет собой двоичное число с младшим битом внизу. Светлые пиксели представляют собой единицы, а темные пиксели - нули.

Рядов

• Сумма элементов одной строки в два раза больше суммы предшествующей ей строки. Например, строка 0 (самая верхняя строка) имеет значение 1, строка 1 имеет значение 2, строка 2 имеет значение 4 и так далее. Это потому, что каждый элемент в строке создает два элемента в следующей строке: один слева и один справа. Сумма элементов строкип равно 2^п.
• Взяв произведение элементов в каждой строке, последовательность продуктов (последовательность A001142 в OEIS ) связана с основанием натурального логарифма, е.^[17][18] В частности, определите последовательность s_п следующее:

${\displaystyle s_{n}=\prod _{k=0}^{n}{\binom {n}{k}}=\prod _{k=0}^{n}{\frac {n!}{k!(n-k)!}}~,~n\geq 0.}$

Тогда соотношение последовательных рядов продуктов равно

${\displaystyle {\frac {s_{n+1}}{s_{n}}}={\frac {(n+1)!^{(n+2)}\prod _{k=0}^{n+1}{k!^{-2}}}{n!^{(n+1)}\prod _{k=0}^{n}{k!^{-2}}}}={\frac {(n+1)^{n}}{n!}}}$

и отношение этих соотношений равно

${\displaystyle {\frac {(s_{n+1})(s_{n-1})}{(s_{n})^{2}}}=\left({\frac {n+1}{n}}\right)^{n},~n\geq 1.}$

Правая часть приведенного выше уравнения принимает форму предельного определения е

${\displaystyle {\textit {e}}=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}.}$

• Пи можно найти в треугольнике Паскаля через Нилаканта бесконечная серия.^[19]

${\displaystyle \pi =3+\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {\binom {2n+1}{1}}{{\binom {2n+1}{2}}{\binom {2n+2}{2}}}}}$

• Значение строки, если каждая запись считается десятичным разрядом (и числа, превышающие 9, переносятся соответственно), это степень 11 ( 11^п, для строкип). Таким образом, во 2 строке ⟨1, 2, 1⟩ становится 11², пока ⟨1, 5, 10, 10, 5, 1⟩ в пятой строке становится (после переноса) 161051, что составляет 11⁵. Это свойство объясняется установкой Икс = 10 в биномиальном разложении (Икс + 1)^п, и перевод значений в десятичную систему. Но Икс можно выбрать, чтобы строки могли представлять значения в любой основание.
  • В база 3: 1 2 1₃ = 4² (16)
  • ⟨1, 3, 3, 1⟩ → 2 1 0 1₃ = 4³ (64)
  • В база 9: 1 2 1₉ = 10² (100)
  •               1 3 3 1₉ = 10³ (1000)
  • ⟨1, 5, 10, 10, 5, 1⟩ → 1 6 2 1 5 1₉ = 10⁵ (100000)

  В частности (см. Предыдущее свойство), для Икс = 1 стоимость остается постоянный (1^место= 1). Таким образом, записи можно просто добавлять при интерпретации значения строки.

• Некоторые числа в треугольнике Паскаля соотносятся с числами в Треугольник Лозанича.
• Сумма квадратов элементов строкип равно среднему элементу строки2п. Например, 1² + 4² + 6² + 4² + 1² = 70. В общем виде:

${\displaystyle \sum _{k=0}^{n}{n \choose k}^{2}={2n \choose n}.}$

• В любом рядуп, куда п чётно, средний член минус член на две точки слева равняется Каталонский номер в частности (п/2 + 1)й каталонский номер. Например: в строке 4, 6 − 1 = 5, которое является третьим каталонским числом, и 4/2 + 1 = 3.
• В рядп куда п это простое число, все члены в этой строке, кроме единиц, являются кратные изп. Это легко доказать, так как если ${\displaystyle p\in \mathbb {P} }$, тогда п не имеет факторов, кроме 1 и самого себя. Каждая запись в треугольнике является целым числом, поэтому по определению ${\displaystyle (p-k)!}$ и ${\displaystyle k!}$ факторы ${\displaystyle p!\,}$. Однако нет возможности п сам может появиться в знаменателе, поэтому п (или несколько его значений) необходимо оставить в числителе, в результате чего вся запись будет кратна п.
• Паритет: Считать странный термины подрядп, конвертировать п к двоичный. Позволять Икс быть количеством единиц в двоичном представлении. Тогда количество нечетных членов будет 2^Икс. Эти числа являются значениями в Последовательность Гулда.^[20]
• Каждая запись в строке 2^п-1, п ≥ 0, является нечетным.^[21]
• Полярность: Когда элементы строки треугольника Паскаля последовательно складываются и вычитаются, каждая строка со средним числом, то есть строки с нечетным числом целых чисел, дает в результате 0. Например, строка 4 - 1 4 6 4 1, поэтому формула будет иметь вид 6 - (4 + 4) + (1 + 1) = 0; а строка 6 - 1 6 15 20 15 6 1, поэтому формула будет иметь вид 20 - (15 + 15) + (6 + 6) - (1 + 1) = 0. Таким образом, каждая четная строка треугольника Паскаля равна 0, когда вы берете среднее число, затем вычитаете целые числа непосредственно рядом с центром, затем складываете следующие целые числа, затем вычитаете и т. д. и т. д., пока не дойдете до конца строки.

Диагонали

Вывод симплекс числа из выровненного влево треугольника Паскаля

Диагонали треугольника Паскаля содержат фигуральные числа симплексов:

• Диагонали, идущие по левому и правому краям, содержат только единицы.
• Диагонали рядом с диагоналями краев содержат натуральные числа чтобы.
• Двигаясь внутрь, следующая пара диагоналей содержит треугольные числа чтобы.
• Следующая пара диагоналей содержит тетраэдрические числа по порядку, а следующая пара дает числа пентатопа.

${\displaystyle {\begin{aligned}P_{0}(n)&=P_{d}(0)=1,\\P_{d}(n)&=P_{d}(n-1)+P_{d-1}(n)\\&=\sum _{i=0}^{n}P_{d-1}(i)=\sum _{i=0}^{d}P_{i}(n-1).\end{aligned}}}$

Симметрия треугольника означает, что п^th d-мерное число равно d^th п-размерный номер.

Альтернативная формула, не использующая рекурсию, выглядит следующим образом:

${\displaystyle P_{d}(n)={\frac {1}{d!}}\prod _{k=0}^{d-1}(n+k)={n^{(d)} \over d!}={\binom {n+d-1}{d}}}$

куда п^(d) это возрастающий факториал.

Геометрический смысл функции P_d это: P_d(1) = 1 для всех d. Построить d-размерный треугольник (трехмерный треугольник - это тетраэдр ) путем размещения дополнительных точек под начальной точкой, соответствующей P_d(1) = 1. Разместите эти точки аналогично расположению чисел в треугольнике Паскаля. Чтобы найти P_d(Икс), всего Икс точки, составляющие целевую форму. п_d(Икс) тогда равняется общему количеству точек в форме. 0-мерный треугольник - это точка, а одномерный треугольник - это просто линия, и поэтому P₀(Икс) = 1 и P₁(Икс) = Икс, которая представляет собой последовательность натуральных чисел. Количество точек в каждом слое соответствует P_d − 1(Икс).

Вычисление строки или диагонали отдельно

Существуют простые алгоритмы для вычисления всех элементов в строке или диагонали без вычисления других элементов или факториалов.

Вычислить строку ${\displaystyle n}$ с элементами ${\displaystyle {\tbinom {n}{0}}}$, ${\displaystyle {\tbinom {n}{1}}}$, ..., ${\displaystyle {\tbinom {n}{n}}}$, начинать с ${\displaystyle {\tbinom {n}{0}}=1}$. Для каждого последующего элемента значение определяется путем умножения предыдущего значения на дробь с медленно меняющимися числителем и знаменателем:

${\displaystyle {n \choose k}={n \choose k-1}\times {\frac {n+1-k}{k}}.}$

Например, для вычисления строки 5 дроби равны ${\displaystyle {\tfrac {5}{1}}}$,  ${\displaystyle {\tfrac {4}{2}}}$,  ${\displaystyle {\tfrac {3}{3}}}$,  ${\displaystyle {\tfrac {2}{4}}}$ и ${\displaystyle {\tfrac {1}{5}}}$, а значит, элементы ${\displaystyle {\tbinom {5}{0}}=1}$,   ${\displaystyle {\tbinom {5}{1}}=1\times {\tfrac {5}{1}}=5}$,   ${\displaystyle {\tbinom {5}{2}}=5\times {\tfrac {4}{2}}=10}$и т. д. (Остальные элементы легче всего получить с помощью симметрии.)

Чтобы вычислить диагональ, содержащую элементы ${\displaystyle {\tbinom {n}{0}}}$, ${\displaystyle {\tbinom {n+1}{1}}}$, ${\displaystyle {\tbinom {n+2}{2}}}$, ..., снова начинаем с ${\displaystyle {\tbinom {n}{0}}=1}$ и получить последующие элементы умножением на определенные дроби:

${\displaystyle {n+k \choose k}={n+k-1 \choose k-1}\times {\frac {n+k}{k}}.}$

Например, чтобы вычислить диагональ, начинающуюся в ${\displaystyle {\tbinom {5}{0}}}$, дроби равны ${\displaystyle {\tfrac {6}{1}}}$,  ${\displaystyle {\tfrac {7}{2}}}$,  ${\displaystyle {\tfrac {8}{3}}}$, ..., а элементы ${\displaystyle {\tbinom {5}{0}}=1}$,   ${\displaystyle {\tbinom {6}{1}}=1\times {\tfrac {6}{1}}=6}$,   ${\displaystyle {\tbinom {7}{2}}=6\times {\tfrac {7}{2}}=21}$и т. д. Эти элементы по симметрии равны ${\displaystyle {\tbinom {5}{5}}}$, ${\displaystyle {\tbinom {6}{5}}}$, ${\displaystyle {\tbinom {7}{5}}}$, так далее.

Последовательность Фибоначчи в треугольнике Паскаля

Общие закономерности и свойства

Приближение уровня 4 к треугольнику Серпинского, полученное путем закрашивания первых 32 строк треугольника Паскаля белым цветом, если биномиальный коэффициент четный, и черным, если он нечетный.

• Образец, полученный раскрашиванием только нечетных чисел в треугольнике Паскаля, очень похож на фрактал называется Треугольник Серпинского. Это сходство становится все более точным по мере того, как рассматривается больше строк; в пределе, когда количество строк приближается к бесконечности, результирующий шаблон является треугольник Серпинского, предполагающий фиксированный периметр.^[22] В более общем смысле числа могут быть окрашены по-разному в зависимости от того, кратны ли они 3, 4 и т.д .; это приводит к другим подобным образцам.

			10
		10	20

Треугольник Паскаля, наложенный на сетку, дает количество различных путей к каждому квадрату, предполагая, что учитываются только движения вправо и вниз.

• В треугольной части сетки (как на изображениях ниже) количество кратчайших путей сетки от данного узла до верхнего узла треугольника является соответствующей записью в треугольнике Паскаля. На Плинко игровое поле имеет форму треугольника, такое распределение должно давать вероятности выигрыша различных призов.

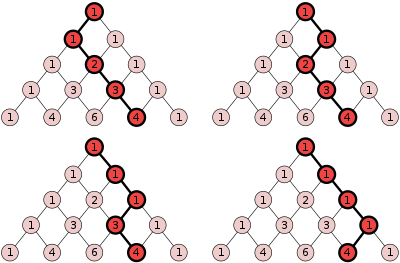
• Если строки треугольника Паскаля выровнены по левому краю, диагональные полосы (отмеченные цветом ниже) суммируются с Числа Фибоначчи.

1
1	1
1	2	1
1	3	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1
1	7	21	35	35	21	7	1

Построение как матричная экспонента

${\displaystyle {\begin{aligned}\exp {\begin{pmatrix}.&.&.&.&.\\1&.&.&.&.\\.&2&.&.&.\\.&.&3&.&.\\.&.&.&4&.\end{pmatrix}}&={\begin{pmatrix}1&.&.&.&.\\1&1&.&.&.\\1&2&1&.&.\\1&3&3&1&.\\1&4&6&4&1\end{pmatrix}}\\e^{counting}&=binomial\end{aligned}}}$

Биномиальная матрица как матричная экспонента. Все точки обозначают 0.

Смотрите также: Матрица Паскаля

Благодаря простой конструкции с помощью факториалов, очень простое представление треугольника Паскаля в терминах матричная экспонента может быть задано: треугольник Паскаля - это экспонента матрицы, которая имеет последовательность 1, 2, 3, 4, ... на его поддиагонали и ноль везде.

Связи с геометрией многогранников

Треугольник Паскаля можно использовать как Справочная таблица для количества элементов (например, кромок и углов) в пределах многогранник (например, треугольник, тетраэдр, квадрат и куб).

Количество элементов симплексов

Давайте начнем с рассмотрения 3-й строки треугольника Паскаля со значениями 1, 3, 3, 1. Двумерный треугольник имеет один двумерный элемент (сам), три одномерных элемента (линии или ребра) и три 0-мерные элементы (вершины, или углы). Значение последней цифры (1) объяснить сложнее (но см. Ниже). Продолжая наш пример, тетраэдр имеет один 3-мерный элемент (сам), четыре 2-мерных элемента (грани), шесть 1-мерных элементов (ребер) и четыре 0-мерных элемента (вершины). Снова складывая последнюю 1, эти значения соответствуют 4-й строке треугольника (1, 4, 6, 4, 1). Линия 1 соответствует точке, а линия 2 соответствует отрезку (диаде). Этот паттерн продолжается до гипер-тетраэдров произвольно больших размеров (известных как симплексы ).

Чтобы понять, почему существует этот паттерн, нужно сначала понять, что процесс построения п-суплекс от (п − 1)-симплекс состоит из простого добавления к последней новой вершине, расположенной так, чтобы эта новая вершина лежала вне пространства исходного симплекса, и соединения ее со всеми исходными вершинами. В качестве примера рассмотрим случай построения тетраэдра из треугольника, последний из элементов которого пронумерован строкой 3 треугольника Паскаля: 1 лицо, 3 края и 3 вершины (значение последней единицы будет объяснено в ближайшее время). Чтобы построить тетраэдр из треугольника, мы располагаем новую вершину над плоскостью треугольника и соединяем эту вершину со всеми тремя вершинами исходного треугольника.

Номер данного размерного элемента в тетраэдре теперь представляет собой сумму двух чисел: сначала номер этого элемента, найденного в исходном треугольнике, плюс количество новых элементов, каждый из которых построен на элементах с меньшим размером исходного треугольника. Таким образом, в тетраэдре количество клетки (многогранные элементы) 0 + 1 = 1; количество лиц 1 + 3 = 4; количество ребер 3 + 3 = 6; количество новых вершин 3 + 1 = 4. Этот процесс суммирования количества элементов данного измерения с элементами меньшего измерения для получения количества первых, найденных в следующем более высоком симплексе, эквивалентен процессу суммирования двух соседних чисел в строке треугольника Паскаля для получения номер ниже. Таким образом, значение последнего числа (1) в строке треугольника Паскаля становится понятным как представляющее новую вершину, которая должна быть добавлена ​​к симплексу, представленному этой строкой, чтобы получить следующий более высокий симплекс, представленный следующей строкой. Эта новая вершина присоединяется к каждому элементу в исходном симплексе, чтобы получить новый элемент одного более высокого измерения в новом симплексе, и это источник шаблона, который оказался идентичным узору в треугольнике Паскаля. «Дополнительный» 1 в ряду можно представить как симплекс -1, уникальный центр симплекса, который когда-либо дает начало новой вершине и новому измерению, давая новый симплекс с новым центром.

Количество элементов гиперкубов

Аналогичная картина наблюдается в отношении квадраты, в отличие от треугольников. Чтобы найти образец, нужно построить аналог треугольника Паскаля, элементы которого являются коэффициентами (Икс + 2)^{Номер строки}, вместо (Икс + 1)^{Номер строки}. Это можно сделать двумя способами. Более простой вариант - начать с строки 0 = 1 и строки 1 = 1, 2. Продолжайте строить аналоговые треугольники по следующему правилу:

${\displaystyle {n \choose k}=2\times {n-1 \choose k-1}+{n-1 \choose k}.}$

То есть выберите пару чисел в соответствии с правилами треугольника Паскаля, но перед сложением удвойте число слева. Это приводит к:

${\displaystyle {\begin{matrix}{\text{ 1}}\\{\text{ 1}}\quad {\text{ 2}}\\{\text{ 1}}\quad {\text{ 4}}\quad {\text{ 4}}\\{\text{ 1}}\quad {\text{ 6}}\quad {\text{ 12}}\quad {\text{ 8}}\\{\text{ 1}}\quad {\text{ 8}}\quad {\text{ 24}}\quad {\text{ 32}}\quad {\text{ 16}}\\{\text{ 1}}\quad {\text{ 10}}\quad {\text{ 40}}\quad {\text{ 80}}\quad {\text{ 80}}\quad {\text{ 32}}\\{\text{ 1}}\quad {\text{ 12}}\quad {\text{ 60}}\quad 160\quad 240\quad 192\quad {\text{ 64}}\\{\text{ 1}}\quad {\text{ 14}}\quad {\text{ 84}}\quad 280\quad 560\quad 672\quad 448\quad 128\end{matrix}}}$

Другой способ изготовления этого треугольника - начать с треугольника Паскаля и умножить каждую запись на 2.^k, где k - позиция в строке заданного числа. Например, 2-е значение в строке 4 треугольника Паскаля равно 6 (наклон единиц соответствует нулевой записи в каждой строке). Чтобы получить значение, которое находится в соответствующей позиции аналогового треугольника, умножьте 6 на 2^{Номер позиции} = 6 × 2² = 6 × 4 = 24. Теперь, когда аналоговый треугольник построен, количество элементов любой размерности, составляющих произвольно измеренный куб (называется гиперкуб ) можно прочитать из таблицы аналогично треугольнику Паскаля. Например, количество 2-мерных элементов в 2-мерном кубе (квадрате) равно единице, количество 1-мерных элементов (сторон или линий) равно 4, а количество 0-мерных элементов (точек, или вершин) равно 4. Это соответствует 2-й строке таблицы (1, 4, 4). Куб имеет 1 куб, 6 граней, 12 ребер и 8 вершин, что соответствует следующей строке аналогового треугольника (1, 6, 12, 8). Этот образец продолжается бесконечно.

Чтобы понять, почему существует этот шаблон, сначала осознайте, что построение п-куб из (п − 1)-куб делается простым копированием исходной фигуры и смещением ее на некоторое расстояние (для обычного п-куб, длина ребра) ортогональный в пространство исходной фигуры, затем соединяя каждую вершину новой фигуры с соответствующей вершиной оригинала. Этот начальный процесс дублирования является причиной того, почему, чтобы перечислить размерные элементы п-куб, нужно удвоить первое из пары чисел в строке этого аналога треугольника Паскаля, прежде чем суммировать, чтобы получить число ниже. Таким образом, первоначальное удвоение дает количество «исходных» элементов, которые можно найти в следующих более высоких п-куб и, как и раньше, новые элементы строятся на элементах меньшего размера (ребра на вершинах, грани на ребрах и т. д.). Опять же, последнее число в строке представляет количество новых вершин, которые нужно добавить, чтобы сгенерировать следующую, более высокую. п-куб.

В этом треугольнике сумма элементов строки м равно 3^м. Опять же, чтобы использовать элементы строки 4 в качестве примера: 1 + 8 + 24 + 32 + 16 = 81, что равно ${\displaystyle 3^{4}=81}$.

Подсчет вершин в кубе по расстоянию

Каждая строка треугольника Паскаля дает количество вершин на каждом расстоянии от фиксированной вершины в п-мерный куб. Например, в трех измерениях третий ряд (1 3 3 1) соответствует обычному трехмерному куб: фиксация вершины V, есть одна вершина на расстоянии 0 от V (то есть, V сам), три вершины на расстоянии 1, три вершины на расстоянии √2 и одна вершина на расстоянии √3 (вершина напротив V). Вторая строка соответствует квадрату, а строки с большим номером соответствуют гиперкубы в каждом измерении.

Преобразование Фурье греха (Икс)^п+1/Икс

Как указывалось ранее, коэффициенты при (Икс + 1)^п являются n-й строкой треугольника. Теперь коэффициенты при (Икс − 1)^п те же самые, за исключением того, что знак меняется от +1 до -1 и обратно. После соответствующей нормализации такой же шаблон чисел появляется в преобразование Фурье греха (Икс)^п+1/Икс. Точнее: если п ровно, возьмите реальная часть преобразования, и если п странно, возьмите мнимая часть. Тогда результатом будет ступенчатая функция, значения которой (подходящим образом нормированные) даются п-й ряд треугольника с чередованием знаков.^[23] Например, значения ступенчатой ​​функции, полученной в результате:

${\displaystyle \,{\mathfrak {Re}}\left({\text{Fourier}}\left[{\frac {\sin(x)^{5}}{x}}\right]\right)}$

составить 4-й ряд треугольника, чередуя знаки. Это обобщение следующего основного результата (часто используемого в электротехника ):

${\displaystyle \,{\mathfrak {Re}}\left({\text{Fourier}}\left[{\frac {\sin(x)^{1}}{x}}\right]\right)}$

это функция товарного вагона.^[24] Соответствующая строка треугольника - это строка 0, которая состоит только из числа 1.

Если n равно конгруэнтный до 2 или до 3 по модулю 4, то знаки начинаются с -1. Фактически, последовательность (нормированных) первых членов соответствует степеням я, которые совершают цикл вокруг пересечения осей с единичной окружностью в комплексной плоскости:

${\displaystyle \,+i,-1,-i,+1,+i,\ldots \,}$

Элементарный клеточный автомат

Узор, созданный элементарный клеточный автомат с использованием правила 60 - это точно треугольник Паскаля биномиальных коэффициентов, уменьшенный по модулю 2 (черные ячейки соответствуют нечетным биномиальным коэффициентам).^[25] Правило 102 также создает этот образец, когда завершающие нули опущены. Правило 90 создает тот же шаблон, но с пустой ячейкой, разделяющей каждую запись в строках.

Расширения

Треугольник Паскаля можно расширить до отрицательных номеров строк.

Сначала напишите треугольник в следующем виде:

м п	0	1	2	3	4	5	...
0	1	0	0	0	0	0	...
1	1	1	0	0	0	0	...
2	1	2	1	0	0	0	...
3	1	3	3	1	0	0	...
4	1	4	6	4	1	0	...

Затем вытяните столбец единиц вверх:

м п	0	1	2	3	4	5	...
−4	1						...
−3	1						...
−2	1						...
−1	1						...
0	1	0	0	0	0	0	...
1	1	1	0	0	0	0	...
2	1	2	1	0	0	0	...
3	1	3	3	1	0	0	...
4	1	4	6	4	1	0	...

Теперь правило:

${\displaystyle {n \choose m}={n-1 \choose m-1}+{n-1 \choose m}}$

можно изменить на:

${\displaystyle {n-1 \choose m}={n \choose m}-{n-1 \choose m-1}}$

что позволяет вычислить другие записи для отрицательных строк:

м п	0	1	2	3	4	5	...
−4	1	−4	10	−20	35	−56	...
−3	1	−3	6	−10	15	−21	...
−2	1	−2	3	−4	5	−6	...
−1	1	−1	1	−1	1	−1	...
0	1	0	0	0	0	0	...
1	1	1	0	0	0	0	...
2	1	2	1	0	0	0	...
3	1	3	3	1	0	0	...
4	1	4	6	4	1	0	...

Это расширение сохраняет свойство, что значения в м-й столбец рассматривается как функция п подходят по заказу м полином, а именно

${\displaystyle {n \choose m}={\frac {1}{m!}}\prod _{k=0}^{m-1}(n-k)={\frac {1}{m!}}\prod _{k=1}^{m}(n-k+1)}$.

Это расширение также сохраняет то свойство, что значения в п-я строка соответствует коэффициентам при (1 +Икс)^п:

${\displaystyle (1+x)^{n}=\sum _{k=0}^{\infty }{n \choose k}x^{k}\quad |x|<1}$

Например:

${\displaystyle (1+x)^{-2}=1-2x+3x^{2}-4x^{3}+\cdots \quad |x|<1}$

Если рассматривать как серию, ряды отрицательных п расходятся. Однако они все еще Абель суммируемый, суммирование которых дает стандартные значения 2^п. (На самом деле п = -1 строка приводит к Серия Гранди который «суммируется» до 1/2, а п = -2 строки приводит к еще один известный сериал в котором сумма Абеля равна 1/4.)

Другой вариант расширения треугольника Паскаля на отрицательные строки - расширение Другой строка 1 с:

м п	−4	−3	−2	−1	0	1	2	3	4	5	...
−4	1	0	0	0	0	0	0	0	0	0	...
−3		1	0	0	0	0	0	0	0	0	...
−2			1	0	0	0	0	0	0	0	...
−1				1	0	0	0	0	0	0	...
0	0	0	0	0	1	0	0	0	0	0	...
1	0	0	0	0	1	1	0	0	0	0	...
2	0	0	0	0	1	2	1	0	0	0	...
3	0	0	0	0	1	3	3	1	0	0	...
4	0	0	0	0	1	4	6	4	1	0	...

Применение того же правила, что и раньше, приводит к

м п	−4	−3	−2	−1	0	1	2	3	4	5	...
−4	1	0	0	0	0	0	0	0	0	0	...
−3	−3	1	0	0	0	0	0	0	0	0	...
−2	3	−2	1	0	0	0	0	0	0	0	...
−1	−1	1	−1	1	0	0	0	0	0	0	..
0	0	0	0	0	1	0	0	0	0	0	...
1	0	0	0	0	1	1	0	0	0	0	...
2	0	0	0	0	1	2	1	0	0	0	...
3	0	0	0	0	1	3	3	1	0	0	...
4	0	0	0	0	1	4	6	4	1	0	...

Это расширение также обладает такими же свойствами, как

${\displaystyle \exp {\begin{pmatrix}.&.&.&.&.\\1&.&.&.&.\\.&2&.&.&.\\.&.&3&.&.\\.&.&.&4&.\end{pmatrix}}={\begin{pmatrix}1&.&.&.&.\\1&1&.&.&.\\1&2&1&.&.\\1&3&3&1&.\\1&4&6&4&1\end{pmatrix}},}$

у нас есть

${\displaystyle \exp {\begin{pmatrix}.&.&.&.&.&.&.&.&.&.\\-4&.&.&.&.&.&.&.&.&.\\.&-3&.&.&.&.&.&.&.&.\\.&.&-2&.&.&.&.&.&.&.\\.&.&.&-1&.&.&.&.&.&.\\.&.&.&.&0&.&.&.&.&.\\.&.&.&.&.&1&.&.&.&.\\.&.&.&.&.&.&2&.&.&.\\.&.&.&.&.&.&.&3&.&.\\.&.&.&.&.&.&.&.&4&.\end{pmatrix}}={\begin{pmatrix}1&.&.&.&.&.&.&.&.&.\\-4&1&.&.&.&.&.&.&.&.\\6&-3&1&.&.&.&.&.&.&.\\-4&3&-2&1&.&.&.&.&.&.\\1&-1&1&-1&1&.&.&.&.&.\\.&.&.&.&.&1&.&.&.&.\\.&.&.&.&.&1&1&.&.&.\\.&.&.&.&.&1&2&1&.&.\\.&.&.&.&.&1&3&3&1&.\\.&.&.&.&.&1&4&6&4&1\end{pmatrix}}}$

Кроме того, так же, как суммирование по диагонали от нижнего левого до верхнего правого диагоналей матрицы Паскаля дает Числа Фибоначчи, этот второй тип расширения по-прежнему суммируется с числами Фибоначчи для отрицательного индекса.

Любое из этих расширений может быть достигнуто, если мы определим

${\displaystyle {n \choose k}={\frac {n!}{(n-k)!k!}}\equiv {\frac {\Gamma (n+1)}{\Gamma (n-k+1)\Gamma (k+1)}}}$

и принять определенные пределы гамма-функция, ${\displaystyle \Gamma (z)}$.

Смотрите также

• Машина для фасоли, "Квинконкс" Фрэнсиса Гальтона
• Треугольник колокола
• Треугольник Бернулли
• Биномиальное разложение
• Треугольник Эйлера
• Треугольник Флойда
• Биномиальный коэффициент Гаусса
• Гармонический треугольник Лейбница
• Кратности вхождений в треугольнике Паскаля (Гипотеза певца)
• Матрица Паскаля
• Пирамида паскаля
• Симплекс Паскаля
• Протонный ЯМР, одно приложение треугольника Паскаля
• (2,1) -Треугольник Паскаля
• Теорема о звезде Давида
• Трехчленное разложение
• Трехчленный треугольник

Рекомендации

1. Морис Винтерниц, История индийской литературы, Vol. III
2. Кулидж, Дж. Л. (1949), «История биномиальной теоремы», Американский математический ежемесячник, 56 (3): 147–157, Дои:10.2307/2305028, JSTOR  2305028, МИСТЕР  0028222.
3. Питер Фокс (1998). Библиотека Кембриджского университета: великие коллекции. Издательство Кембриджского университета. п. 13. ISBN  978-0-521-62647-7.
4. Биномиальный коэффициент ${\displaystyle \scriptstyle {n \choose k}}$ обычно устанавливается равным нулю, если k либо меньше нуля, либо больше п.
5. Треугольник Паскаля | Резюме мира математики
6. А. В. Ф. Эдвардс. Арифметический треугольник Паскаля: история математической идеи. JHU Press, 2002. Страницы 30–31.
7. Эдвардс, А. В. Ф. (2013), «Арифметический треугольник», Уилсон, Робин; Уоткинс, Джон Дж. (Ред.), Комбинаторика: древнее и современное, Oxford University Press, стр. 166–180..
8. Александр Завайра; Гэвин Хичкок (2008). Букварь для олимпиад по математике. Издательство Оксфордского университета. п. 237. ISBN  978-0-19-156170-2.
9. Селин, Хелайн (12 марта 2008 г.). Энциклопедия истории науки, техники и медицины в незападных культурах. Springer Science & Business Media. п. 132. Bibcode:2008ест.книга ..... S. ISBN  9781402045592.
10. Развитие арабской математики между арифметикой и алгеброй - Р. Рашед «Стр. 63»
11. Сидоли, Натан; Браммелен, Глен Ван (30 октября 2013 г.). Из Александрии через Багдад: Обзоры и исследования древнегреческих и средневековых исламских математических наук в честь Дж. Л. Берггрена. Springer Science & Business Media. п. 54. ISBN  9783642367366.
12. Кеннеди, Э. (1966). Омар Хайям. Учитель математики 1958. Национальный совет учителей математики. С. 140–142. JSTOR  i27957284.
13. Вайсштейн, Эрик В. (2003). CRC краткая энциклопедия математики, п. 2169. ISBN  978-1-58488-347-0.
14. Хьюз, Варнава (1 августа 1989 г.). «Арифметический треугольник Иордана де Немора». Historia Mathematica. 16 (3): 213–223. Дои:10.1016/0315-0860(89)90018-9.
15. Смит, Карл Дж. (2010), Природа математики, Cengage Learning, стр. 10, ISBN  9780538737586.
16. Фаулер, Дэвид (Январь 1996 г.). «Биномиальная функция коэффициента». Американский математический ежемесячник. 103 (1): 1–17. Дои:10.2307/2975209. JSTOR  2975209. См., В частности, стр. 11.
17. Братья, Х. Дж. (2012), «Нахождение е в треугольнике Паскаля», Математический журнал, 85: 51, Дои:10.4169 / math.mag.85.1.51, S2CID  218541210.
18. Братья, Х. Дж. (2012), "Треугольник Паскаля: Скрытая история".е", Математический вестник, 96: 145–148, Дои:10.1017 / S0025557200004204.
19. Фостер, Т. (2014), «Следы Нилаканты в треугольнике Паскаля», Учитель математики, 108: 247, Дои:10.5951 / mathteacher.108.4.0246
20. Файн, Н. Дж. (1947), "Биномиальные коэффициенты по простому модулю", Американский математический ежемесячный журнал, 54 (10): 589–592, Дои:10.2307/2304500, JSTOR  2304500, МИСТЕР  0023257. См., В частности, теорему 2, которая дает обобщение этого факта для всех простых модулей.
21. Хинц, Андреас М. (1992), «Треугольник Паскаля и Ханойская башня», Американский математический ежемесячник, 99 (6): 538–544, Дои:10.2307/2324061, JSTOR  2324061, МИСТЕР  1166003. Хинц приписывает это наблюдение книге 1891 г. Эдуард Лукас, Теория Номбр (стр. 420).
22. Вольфрам, С. (1984). «Теория вычислений клеточных автоматов». Comm. Математика. Phys. 96 (1): 15–57. Bibcode:1984CMaPh..96 ... 15Вт. Дои:10.1007 / BF01217347. S2CID  121021967.
23. Для аналогичного примера см., Например, Хор, П. Дж. (1983), "Подавление растворителем в ядерном магнитном резонансе с преобразованием Фурье", Журнал магнитного резонанса, 55 (2): 283–300, Bibcode:1983JMagR..55..283H, Дои:10.1016/0022-2364(83)90240-8.
24. Карл, Джон Х. (2012), Введение в цифровую обработку сигналов, Elsevier, стр. 110, ISBN  9780323139595.
25. Вольфрам, С. (2002). Новый вид науки. Шампейн Иллинойс: Вольфрам Медиа. стр.870, 931–2.

внешняя ссылка

• «Треугольник Паскаля», Энциклопедия математики, EMS Press, 2001 [1994]
• Вайсштейн, Эрик В. «Треугольник Паскаля». MathWorld.
• Схема семи квадратов умножения по старому методу (из Ssu Yuan Yü Chien of Chu Shi-Chieh, 1303 г., с изображением первых девяти рядов треугольника Паскаля)
• Трактат Паскаля об арифметическом треугольнике (изображения страниц трактата Паскаля, 1654 г .; резюме )