Метод Гаусса - Gausss method - Wikipedia

В орбитальная механика (подполе небесная механика ), Метод Гаусса используется для предварительного определение орбиты по крайней мере, из трех наблюдений (большее количество наблюдений увеличивает точность определения орбиты) интересующего объекта на орбите в три разных периода времени. Требуемая информация - время наблюдений, векторы положения точек наблюдения (в Экваториальная система координат ), вектор направляющего косинуса движущегося по орбите тела из точек наблюдения (из топоцентрической экваториальной системы координат) и общие физические данные.

Карл Фридрих Гаусс разработал важные математические методы (обобщенные в методах Гаусса), которые специально использовались для определения орбиты Церера. Показанный ниже метод представляет собой определение орбиты движущегося по орбите тела вокруг фокального тела, откуда были взяты наблюдения, тогда как метод определения орбиты Цереры требует немного больше усилий, поскольку наблюдения были взяты из земной шар пока Церера вращается вокруг солнце.

Вектор позиции наблюдателя

Вектор положения наблюдателя (в Экваториальная система координат ) точек наблюдения можно определить из широта и местное звездное время (из Топоцентрическая система координат ) на поверхности фокального тела орбитального тела (например, Земли) посредством:

${\displaystyle \mathbf {R_{n}} =\left[{R_{e} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\cos \phi _{n}(\cos \theta _{n}\ \mathbf {\hat {I}} +\sin \theta _{n}\ \mathbf {\hat {J}} )+\left[{R_{e}(1-f)^{2} \over {\sqrt {1-(2f-f^{2})\sin ^{2}\phi _{n}}}}+H_{n}\right]\sin \phi _{n}\ \mathbf {\hat {K}} }$

Геодезическая широта

Геоцентрическая широта

или же

${\displaystyle \mathbf {R_{n}} =R_{e}\cos \phi '_{n}\cos \theta _{n}\ \mathbf {\hat {I}} +R_{e}\cos \phi '_{n}\sin \theta _{n}\ \mathbf {\hat {J}} +R_{e}\sin \phi '_{n}\ \mathbf {\hat {K}} }$

куда,

• ${\displaystyle \mathbf {R_{n}} }$ - соответствующий вектор положения наблюдателя (в экваториальной системе координат)
• ${\displaystyle R_{e}}$ - экваториальный радиус тела (например, 6378 км для Земли)
• ${\displaystyle f}$ сжатость (или сплющивание ) тела (например, 0,003353 для Земли)
• ${\displaystyle \phi _{n}}$ это геодезическая широта (угол между нормальной плоскостью и экваториальной плоскостью)
• ${\displaystyle \phi '_{n}}$ это геоцентрическая широта (угол между радиусом и экваториальной плоскостью)
• ${\displaystyle H_{n}}$ это высота
• ${\displaystyle \theta _{n}}$ это местное звездное время

Вектор косинуса направления вращения тела

Прямое восхождение (синий) и склонение (зеленый), если смотреть снаружи небесная сфера

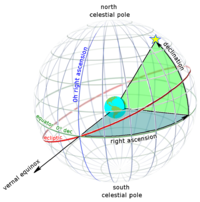
Вектор косинуса направления орбитального тела может быть определен из прямое восхождение и склонение (из топоцентрической экваториальной системы координат) орбитального тела из точек наблюдения через:

${\displaystyle \mathbf {{\hat {\rho }}_{n}} =\cos \delta _{n}\cos \alpha _{n}\ \mathbf {\hat {I}} +\cos \delta _{n}\sin \alpha _{n}\ \mathbf {\hat {J}} +\sin \delta _{n}\ \mathbf {\hat {K}} }$

куда,

• ${\displaystyle \mathbf {{\hat {\rho }}_{n}} }$ - соответствующий единичный вектор в направлении вектора положения ${\displaystyle \rho }$ (от точки наблюдения до орбитального тела в топоцентрической экваториальной системе координат)
• ${\displaystyle \delta _{n}}$ соответствующее склонение
• ${\displaystyle \alpha _{n}}$ соответствующее прямое восхождение

Метод Гаусса алгоритм предварительного определения орбиты

Первоначальный вывод начинается с добавления вектора для определения вектора положения движущегося по орбите тела. Тогда исходя из сохранения угловой момент и Кеплеровская орбита принципов (в которых говорится, что орбита лежит в двухмерной плоскости в трехмерном пространстве) устанавливается линейная комбинация упомянутых векторов положения. Кроме того, связь между положением тела и вектором скорости на Коэффициенты Лагранжа используется, что приводит к использованию указанных коэффициентов. Затем с помощью векторной обработки и алгебры были выведены следующие уравнения. Для получения подробной информации обратитесь к Кертису.^[1]

ПРИМЕЧАНИЕ. Метод Гаусса - это предварительное определение орбиты с упором на предварительное. Аппроксимация коэффициентов Лагранжа и ограничения требуемых условий наблюдения (т. Е. Незначительная кривизна дуги между наблюдениями, см. Gronchi^[2] подробнее) вызывает неточности. Однако метод Гаусса можно улучшить, повысив точность подкомпонентов, таких как решение Уравнение Кеплера. Еще один способ повысить точность - увеличить количество наблюдений.

Шаг 1

Вычислите временные интервалы, вычтите время между наблюдениями:

${\displaystyle \tau _{1}=t_{1}-t_{2}}$

${\displaystyle \tau _{3}=t_{3}-t_{2}}$

${\displaystyle \tau =t_{3}-t_{1}}$

куда

• ${\displaystyle \tau _{n}}$ это временной интервал
• ${\displaystyle t_{n}}$ соответствующее время наблюдения

Шаг 2

Перекрестное произведение относительно правой системы координат

Вычислить перекрестные произведения, взять перекрестные произведения направления единицы наблюдения (порядок имеет значение):

${\displaystyle \mathbf {p_{1}} =\mathbf {{\hat {\rho }}_{2}} \times \mathbf {{\hat {\rho }}_{3}} }$

${\displaystyle \mathbf {p_{2}} =\mathbf {{\hat {\rho }}_{1}} \times \mathbf {{\hat {\rho }}_{3}} }$

${\displaystyle \mathbf {p_{3}} =\mathbf {{\hat {\rho }}_{1}} \times \mathbf {{\hat {\rho }}_{2}} }$

куда

• ${\displaystyle \mathbf {a} \times \mathbf {b} }$ это перекрестное произведение векторов ${\displaystyle \mathbf {a} {\text{ and }}\mathbf {b} }$
• ${\displaystyle \mathbf {p_{n}} }$ - соответствующий вектор векторного произведения
• ${\displaystyle \mathbf {{\hat {\rho }}_{n}} }$ - соответствующий единичный вектор

Шаг 3

Три вектора, определяющие параллелепипед. Величина тройного произведения, ${\displaystyle |\mathbf {a} \cdot (\mathbf {b} \times \mathbf {c} )|}$, описывает объем.

Вычислите общую скалярную величину (тройное скалярное произведение), возьмите скалярное произведение первого единичного вектора наблюдений на векторное произведение второго и третьего единичных векторов наблюдений:

${\displaystyle D_{0}=\mathbf {{\hat {\rho }}_{1}} \cdot \mathbf {p_{1}} =\mathbf {{\hat {\rho }}_{1}} \cdot (\mathbf {{\hat {\rho }}_{2}} \times \mathbf {{\hat {\rho }}_{3}} )}$

куда

• ${\displaystyle \mathbf {a} \cdot \mathbf {b} }$ это скалярное произведение векторов ${\displaystyle \mathbf {a} {\text{ and }}\mathbf {b} }$
• ${\displaystyle D_{0}}$ общий скаляр тройное произведение
• ${\displaystyle \mathbf {p_{n}} }$ - соответствующий вектор векторного произведения
• ${\displaystyle \mathbf {{\hat {\rho }}_{n}} }$ - соответствующий единичный вектор

Шаг 4

Вычислите девять скалярных величин (аналогично шагу 3):

${\displaystyle D_{11}=\mathbf {R_{1}} \cdot \mathbf {p_{1}} \qquad D_{12}=\mathbf {R_{1}} \cdot \mathbf {p_{2}} \qquad D_{13}=\mathbf {R_{1}} \cdot \mathbf {p_{3}} }$

${\displaystyle D_{21}=\mathbf {R_{2}} \cdot \mathbf {p_{1}} \qquad D_{22}=\mathbf {R_{2}} \cdot \mathbf {p_{2}} \qquad D_{23}=\mathbf {R_{2}} \cdot \mathbf {p_{3}} }$

${\displaystyle D_{31}=\mathbf {R_{3}} \cdot \mathbf {p_{1}} \qquad D_{32}=\mathbf {R_{3}} \cdot \mathbf {p_{2}} \qquad D_{33}=\mathbf {R_{3}} \cdot \mathbf {p_{3}} }$

куда

• ${\displaystyle D_{mn}}$ - соответствующие скалярные величины
• ${\displaystyle \mathbf {R_{m}} }$ - соответствующий вектор положения наблюдателя
• ${\displaystyle \mathbf {p_{n}} }$ - соответствующий вектор векторного произведения

Шаг 5

Вычислить скалярные коэффициенты положения:

${\displaystyle A={\frac {1}{D_{0}}}\left(-D_{12}{\frac {\tau _{3}}{\tau }}+D_{22}+D_{32}{\frac {\tau _{1}}{\tau }}\right)}$

${\displaystyle B={\frac {1}{6D_{0}}}\left[D_{12}\left(\tau _{3}^{2}-\tau ^{2}\right){\frac {\tau _{3}}{\tau }}+D_{32}\left(\tau ^{2}-\tau _{1}^{2}\right){\frac {\tau _{1}}{\tau }}\right]}$

${\displaystyle E=\mathbf {R_{2}} \cdot \mathbf {{\hat {\rho }}_{2}} }$

куда

• ${\displaystyle A{\text{, }}B{\text{, and }}E}$ являются скалярными позиционными коэффициентами
• ${\displaystyle D_{0}}$ - обычная скалярная величина
• ${\displaystyle D_{mn}}$ - соответствующие скалярные величины
• ${\displaystyle \tau _{n}}$ это временной интервал
• ${\displaystyle R_{n}}$ - соответствующий вектор положения наблюдателя
• ${\displaystyle \mathbf {{\hat {\rho }}_{n}} }$ - соответствующий единичный вектор

Шаг 6

Вычислите квадрат скалярного расстояния второго наблюдения, взяв скалярное произведение вектора положения второго наблюдения:

${\displaystyle {R_{2}}^{2}=\mathbf {R_{2}} \cdot \mathbf {R_{2}} }$

куда

• ${\displaystyle {R_{2}}^{2}}$ это квадрат расстояния второго наблюдения
• ${\displaystyle \mathbf {R_{2}} }$ - вектор положения второго наблюдения

Шаг 7

Вычислите коэффициенты полинома скалярного расстояния для второго наблюдения орбитального тела:

${\displaystyle a=-\left(A^{2}+2AE+{R_{2}}^{2}\right)}$

${\displaystyle b=-2\mu B(A+E)}$

${\displaystyle c=-\mu ^{2}B^{2}}$

куда

• ${\displaystyle a{\text{, }}b{\text{, and }}c}$ - коэффициенты полинома скалярного расстояния для второго наблюдения орбитального тела
• ${\displaystyle A{\text{, }}B{\text{, and }}E}$ являются скалярными позиционными коэффициентами
• ${\displaystyle \mu }$ это гравитационный параметр фокального тела орбитального тела

Шаг 8

Найдите корень скалярного полинома расстояния для второго наблюдения вращающегося тела:

${\displaystyle {r_{2}}^{8}+a{r_{2}}^{6}+b{r_{2}}^{3}+c=0}$

куда

• ${\displaystyle r_{2}}$ - скалярное расстояние для второго наблюдения орбитального тела (его и его вектора, р₂, находятся в экваториальной системе координат)
• ${\displaystyle a{\text{, }}b{\text{, and }}c}$ коэффициенты, как указано ранее

Для поиска корня можно использовать различные методы, предлагаемый метод - Метод Ньютона-Рафсона. Корень должен быть физически возможным (то есть не отрицательным и не сложным), и если подходят несколько корней, каждый должен быть оценен и сравнен с любыми доступными данными, чтобы подтвердить их достоверность.

Шаг 9

Рассчитайте наклонный диапазон, расстояние от точки наблюдателя до орбитального тела в соответствующее время:

${\displaystyle \rho _{1}={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{31}{\dfrac {\tau _{1}}{\tau _{3}}}+D_{21}{\dfrac {\tau }{\tau _{3}}}\right){r_{2}}^{3}+\mu D_{31}\left(\tau ^{2}-{\tau _{1}}^{2}\right){\dfrac {\tau _{1}}{\tau _{3}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{3}}^{2}\right)}}-D_{11}\right]}$

${\displaystyle \rho _{2}=A+{\frac {\mu B}{{r_{2}}^{3}}}}$

${\displaystyle \rho _{3}={\frac {1}{D_{0}}}\left[{\frac {6\left(D_{13}{\dfrac {\tau _{3}}{\tau _{1}}}-D_{23}{\dfrac {\tau }{\tau _{1}}}\right){r_{2}}^{3}+\mu D_{13}\left(\tau ^{2}-{\tau _{3}}^{2}\right){\dfrac {\tau _{3}}{\tau _{1}}}}{6{r_{2}}^{3}+\mu \left(\tau ^{2}-{\tau _{1}}^{2}\right)}}-D_{33}\right]}$

куда

• ${\displaystyle \rho _{n}}$ соответствующий наклонный диапазон (он и его вектор, ${\displaystyle \mathbf {\rho _{n}} }$, находятся в топоцентрической экваториальной системе координат)
• ${\displaystyle D_{0}}$ - обычная скалярная величина
• ${\displaystyle D_{mn}}$ - соответствующие скалярные величины
• ${\displaystyle \tau _{(n)}}$ это временной интервал
• ${\displaystyle r_{2}}$ - скалярное расстояние для второго наблюдения орбитального тела
• ${\displaystyle \mu }$ это гравитационный параметр фокального тела орбитального тела

Шаг 10

Вычислите векторы положения тела на орбите, добавив вектор положения наблюдателя к вектору наклонного направления (который представляет собой наклонное расстояние, умноженное на вектор наклонного направления):

${\displaystyle \mathbf {r_{1}} =\mathbf {R_{1}} +\rho _{1}\mathbf {{\hat {\rho }}_{1}} }$

${\displaystyle \mathbf {r_{2}} =\mathbf {R_{2}} +\rho _{2}\mathbf {{\hat {\rho }}_{2}} }$

${\displaystyle \mathbf {r_{3}} =\mathbf {R_{3}} +\rho _{3}\mathbf {{\hat {\rho }}_{3}} }$

куда

• ${\displaystyle \mathbf {r_{n}} }$ - соответствующий вектор положения тела на орбите (в Экваториальная система координат )
• ${\displaystyle \mathbf {R_{n}} }$ - соответствующий вектор положения наблюдателя
• ${\displaystyle \rho _{n}}$ соответствующий наклонный диапазон
• ${\displaystyle \mathbf {{\hat {\rho }}_{n}} }$ - соответствующий единичный вектор

Шаг 11

Рассчитайте коэффициенты Лагранжа:

${\displaystyle f_{1}\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{2}}$

${\displaystyle f_{3}\approx 1-{\frac {1}{2}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{2}}$

${\displaystyle g_{1}\approx \tau _{1}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{1}}^{3}}$

${\displaystyle g_{3}\approx \tau _{3}-{\frac {1}{6}}{\frac {\mu }{{r_{2}}^{3}}}{\tau _{3}}^{3}}$

куда,

• ${\displaystyle f_{1}}$, ${\displaystyle f_{3}}$, ${\displaystyle g_{1}}$ и ${\displaystyle g_{3}}$ являются Коэффициенты Лагранжа (это только первые два члена выражения ряда в предположении малого временного интервала)
• ${\displaystyle \mu }$ это гравитационный параметр фокального тела орбитального тела
• ${\displaystyle r_{2}}$ - скалярное расстояние для второго наблюдения орбитального тела
• ${\displaystyle \tau _{(n)}}$ это временной интервал

Шаг 12

Вычислите вектор скорости для второго наблюдения орбитального тела:

${\displaystyle \mathbf {v_{2}} ={\frac {1}{f_{1}g_{3}-f_{3}g_{1}}}\left(-f_{3}\mathbf {r_{1}} +f_{1}\mathbf {r_{3}} \right)}$

куда

• ${\displaystyle \mathbf {v_{2}} }$ - вектор скорости для второго наблюдения орбитального тела (в Экваториальная система координат )
• ${\displaystyle f_{1}}$, ${\displaystyle f_{3}}$, ${\displaystyle g_{1}}$ и ${\displaystyle g_{3}}$ являются Коэффициенты Лагранжа
• ${\displaystyle \mathbf {r_{n}} }$ - соответствующий вектор орбитального положения тела

Шаг 13

В орбитальные векторы состояния были найдены вектор положения (r2) и скорости (v2) для второго наблюдения орбитального тела. С помощью этих двух векторов можно найти элементы орбиты и определить орбиту.

Рекомендации

1. Кертис, Говард Д. Орбитальная механика для студентов инженерных специальностей. Оксфорд: Elsevier Butterworth-Heinemann, 2005. Печать.
2. Гронки, Джованни Ф .. "Классическое и современное определение орбиты астероидов". Труды Международного астрономического союза, 2004.IAUC196 (2004): 1-11. Распечатать.

• Дер, Гим Дж. «Новые только углы алгоритмы для определения начальной орбиты». Конференция Advanced Maui Optical and Space Surveillance Technologies Conference. (2012). Распечатать.