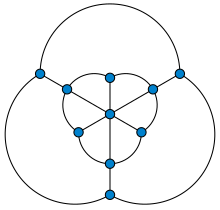
Граф Голомба - Golomb graph

Граф Голомба
Названный в честь	Соломон В. Голомб
Вершины	10
Края	18
Хроматическое число	4
Характеристики	многогранник единичное расстояние
Таблица графиков и параметров

В теория графов, то Граф Голомба это многогранный граф с 10 вершины и 18 края. Он назван в честь Соломон В. Голомб, кто его построил (с не-планарный встраивание) как график единичного расстояния требуется четыре цвета в любом раскраска графика. Таким образом, как и более простой Шпиндель Мозера, это дает нижнюю оценку для Проблема Хадвигера – Нельсона: раскрашивание точек Евклидова плоскость так что каждый блок отрезок имеет разноцветные конечные точки, требуется как минимум четыре цвета.^[1]

Строительство

4-раскраска графа Голомба, нарисованного как граф единичных расстояний

Метод построения графа Голомба как графа единичных расстояний путем рисования внешнего правильного многоугольника, соединенного с внутренним скрученным многоугольником или звездообразным многоугольником, также использовался для представлений единичных расстояний. Граф Петерсена и из обобщенные графы Петерсена.^[2] Как и в случае шпинделя Мозера, координаты вложения графа Голомба на единичное расстояние могут быть представлены в виде квадратичное поле ${\displaystyle \mathbb {Q} [{\sqrt {33}}]}$.^[3]

Дробное окрашивание

В дробное хроматическое число графа Голомба составляет 10/3. Тот факт, что это число, по крайней мере, такое большое, следует из того факта, что граф имеет 10 вершин, не более трех из которых могут находиться в любом независимом множестве. Тот факт, что это число не превышает этого значения, следует из того факта, что можно найти 10 независимых трех вершинных наборов, каждая из которых находится ровно в трех из этих наборов. Это дробное хроматическое число меньше числа 7/2 для веретено Мозера и меньшее, чем дробное хроматическое число диаграммы единичных расстояний плоскости, которое ограничено между 3,6190 и 4,3599.^[4]

Рекомендации

1. Сойфер Александр (2008), Математическая книжка-раскраска: математика раскраски и красочная жизнь ее создателей, Нью-Йорк: Springer, стр. 19, ISBN  978-0-387-74640-1
2. Читник, Арджана; Хорват, Борис; Писанский, Томаж (2012), «Все обобщенные графы Петерсена являются графами единичных расстояний», Журнал Корейского математического общества, 49 (3): 475–491, Дои:10.4134 / JKMS.2012.49.3.475, МИСТЕР  2953031
3. Пегг, Эд, младший (21 декабря 2017 г.), "Шпиндели Мозера, графики Голомба и корень 33", Вольфрам Демонстрационный проект
4. Крэнстон, Дэниел В .; Rabern, Landon (2017), "Дробное хроматическое число плоскости", Комбинаторика, 37 (5): 837–861, arXiv:1501.01647, Дои:10.1007 / s00493-016-3380-3, МИСТЕР  3737371

внешняя ссылка

• Вайсштейн, Эрик В. «График Голомба». MathWorld.