Хеш-таблица - Hash table

Не путать с Список хэшей или же Хеш-дерево.

"Rehash" перенаправляется сюда. Для Южный парк эпизод, см. Рехаш (Южный парк). Для команды IRC см. Список команд Internet Relay Chat § REHASH.

Хеш-таблица
Тип	Неупорядоченный ассоциативный массив
Изобрел	1953
Сложность времени в нотация большой O
Алгоритм Средний Худший случай Космос O (п)[1] O (п) Поиск О (1) O (п) Вставлять О (1) O (п) Удалить О (1) O (п)

Маленькая телефонная книга в виде хеш-таблицы

В вычисление, а хеш-таблица (хеш-карта) это структура данных который реализует ассоциативный массив абстрактный тип данных, структура, которая может отображать ключи к значения. В хеш-таблице используется хеш-функция вычислить индекс, также называемый хэш-код, в массив ведра или же слоты, из которого можно найти желаемое значение. Во время поиска ключ хешируется, и полученный хеш указывает, где хранится соответствующее значение.

В идеале хеш-функция будет назначать каждый ключ уникальному сегменту, но в большинстве конструкций хеш-таблиц используется несовершенная хеш-функция, которая может вызвать хеширование. столкновения где хеш-функция генерирует один и тот же индекс для более чем одного ключа. Такие столкновения обычно каким-то образом компенсируются.

В хеш-таблице с правильными размерами средняя стоимость (количество инструкции ) для каждого поиска не зависит от количества элементов, хранящихся в таблице. Многие конструкции хеш-таблиц также позволяют произвольно вставлять и удалять пары ключ-значение в (амортизированный^[2]) постоянная средняя стоимость операции.^[3][4]

Во многих ситуациях хеш-таблицы оказываются в среднем более эффективными, чем деревья поиска или любой другой стол структура поиска. По этой причине они широко используются во многих компьютерных системах. программного обеспечения, особенно для ассоциативные массивы, индексация базы данных, тайники, и наборы.

Хеширование

Основная статья: Хеш-функция

Идея хеширования состоит в том, чтобы распределить записи (пары ключ / значение) по массиву ведра. По заданному ключу алгоритм вычисляет индекс что подсказывает, где можно найти запись:

индекс = f (ключ, размер_массива)

Часто это делается в два этапа:

hash = hashfunc (ключ) index = hash% array_size

В этом методе хэш не зависит от размера массива, и тогда уменьшенный к индексу (число между 0 и array_size - 1) с использованием оператор по модулю (%).

В случае, если размер массива равен сила двух, остаток сводится к маскировка, что увеличивает скорость, но может увеличить проблемы из-за плохой хэш-функции.^[5]

Выбор хеш-функции

Основное требование - функция должна обеспечивать равномерное распределение хеш-значений. Неравномерное распределение увеличивает количество столкновений и стоимость их разрешения. Однородность иногда трудно обеспечить при проектировании, но ее можно оценить эмпирически с помощью статистических тестов, например, Критерий хи-квадрат Пирсона для дискретных равномерных распределений.^[6][7]

Распределение должно быть равномерным только для размеров таблиц, которые встречаются в приложении. В частности, если используется динамическое изменение размера с точным удвоением и уменьшением вдвое размера таблицы, то хеш-функция должна быть однородной только тогда, когда размер равен сила двух. Здесь индекс может быть вычислен как некоторый диапазон бит хеш-функции. С другой стороны, некоторые алгоритмы хеширования предпочитают, чтобы размер простое число.^[8] Операция по модулю может обеспечить некоторое дополнительное перемешивание; это особенно полезно при плохой хэш-функции.

За открытая адресация схем, хеш-функции также следует избегать кластеризация, отображение двух или более ключей в последовательные слоты. Такая кластеризация может привести к резкому увеличению стоимости поиска, даже если коэффициент загрузки низкий, а коллизии нечасты. Популярный мультипликативный хеш^[3] утверждается, что имеет особенно плохое поведение при кластеризации.^[8]

Криптографические хеш-функции как полагают, обеспечивают хорошие хеш-функции для таблиц любого размера, либо по модулю сокращение или на битовая маскировка^{[нужна цитата ]}. Они также могут быть уместны, если есть риск того, что злоумышленники попытаются саботаж сетевой сервис путем отправки запросов, предназначенных для генерации большого количества конфликтов в хэш-таблицах сервера. Однако риска саботажа можно избежать и более дешевыми методами (такими как применение секретного соль к данным, или используя универсальная хеш-функция ). Недостатком криптографических хеш-функций является то, что они часто медленнее вычисляются, что означает, что в случаях, когда единообразие для любой size не является обязательным, предпочтительнее использовать некриптографическую хеш-функцию.^{[нужна цитата ]}

Идеальная хеш-функция

Если все ключи известны заранее, идеальная хеш-функция можно использовать для создания идеальной хеш-таблицы, не имеющей коллизий. Если минимальное идеальное хеширование используется любое место в хеш-таблице.

Идеальное хеширование позволяет постоянное время поиск во всех случаях. Это контрастирует с большинством методов цепочки и открытой адресации, где время поиска в среднем невелико, но может быть очень большим, O (п), например, когда все ключи хэшируются до нескольких значений.

Ключевые статистические данные

Критическая статистика для хеш-таблицы - это коэффициент нагрузки, определяется как

${displaystyle { ext{load factor}}={frac {n}{k}}}$,

куда

• п - количество записей в хэш-таблице.
• k количество ведер.

По мере увеличения коэффициента загрузки хеш-таблица становится медленнее и может даже не работать (в зависимости от используемого метода). Ожидаемый постоянное время Свойство хеш-таблицы предполагает, что коэффициент загрузки не превышает некоторого предела. Для фиксированный количество сегментов, время поиска растет с количеством записей, и поэтому желаемое постоянное время не достигается. В некоторых реализациях решение состоит в том, чтобы автоматически увеличивать (обычно вдвое) размер таблицы при достижении ограничения коэффициента загрузки, что вынуждает повторно хешировать все записи. В качестве реального примера, коэффициент загрузки по умолчанию для HashMap в Java 10 составляет 0,75, что «предлагает хороший компромисс между затратами времени и пространства».^[9]

Во-вторых, помимо коэффициента загрузки, можно исследовать вариацию количества записей в ведре. Например, две таблицы содержат по 1000 записей и 1000 сегментов; у одного есть ровно одна запись в каждой корзине, у другой - все записи в одной и той же корзине. Ясно, что во втором хеширование не работает.

Низкий коэффициент загрузки не особенно выгоден. Когда коэффициент загрузки приближается к 0, доля неиспользуемых областей в хеш-таблице увеличивается, но не обязательно какое-либо снижение стоимости поиска. Это приводит к потере памяти.

Разрешение коллизий

Хеш столкновения практически неизбежны при хешировании случайного подмножества большого набора возможных ключей. Например, если 2450 ключей хешируются в миллион корзин, даже с идеально равномерным случайным распределением, согласно проблема дня рождения вероятность того, что по крайней мере два ключа хешируются в один и тот же слот, составляет примерно 95%.

Поэтому почти все реализации хэш-таблиц имеют некоторую стратегию разрешения конфликтов для обработки таких событий. Ниже описаны некоторые общие стратегии. Все эти методы требуют, чтобы ключи (или указатели на них) хранились в таблице вместе со связанными значениями.

Отдельная цепочка

Коллизия хэша разрешена отдельной цепочкой.

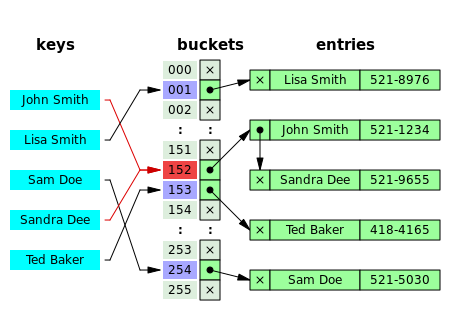
В методе, известном как отдельная цепочка, каждая корзина независима и имеет своего рода список записей с тем же индексом. Время для операций с хеш-таблицей - это время на поиск сегмента (которое постоянно) плюс время для операции со списком.

В большинстве реализаций в корзинах будет несколько записей, если хеш-функция работает правильно. Следовательно, в этих случаях предпочтительны структуры, эффективные во времени и пространстве. Структуры, которые эффективны для довольно большого количества записей в ведре, не нужны или нежелательны. Если такие случаи случаются часто, необходимо исправить функцию хеширования.^[10]

Есть несколько реализаций^[11] которые обеспечивают отличную производительность как для времени, так и для пространства, при среднем количестве элементов в ведре от 5 до 100.

Отдельная цепочка со связанными списками

Связанные хеш-таблицы с связанные списки популярны, потому что они требуют только базовых структур данных с простыми алгоритмами и могут использовать простые хэш-функции, которые не подходят для других методов.^{[нужна цитата ]}

Стоимость операции с таблицей - это сканирование записей выбранной корзины для поиска нужного ключа. Если раздача ключей достаточно однородный, то средний Стоимость поиска зависит только от среднего количества ключей в сегменте, то есть примерно пропорциональна коэффициенту загрузки.

По этой причине связанные хеш-таблицы остаются эффективными, даже если количество записей таблицы п намного больше, чем количество слотов. Например, связанная хеш-таблица с 1000 слотами и 10 000 сохраненных ключей (коэффициент загрузки 10) в пять-десять раз медленнее, чем таблица с 10 000 слотами (коэффициент загрузки 1); но все же в 1000 раз быстрее, чем простой последовательный список.

Для раздельной цепочки наихудший сценарий - когда все записи вставляются в один и тот же сегмент, и в этом случае хеш-таблица неэффективна, а стоимость поиска - это стоимость поиска в структуре данных сегмента. Если последний является линейным списком, процедуре поиска, возможно, придется сканировать все его записи, поэтому стоимость наихудшего случая пропорциональна количеству п записей в таблице.

Цепочки сегментов часто просматриваются последовательно, используя порядок, в котором записи были добавлены в сегмент. Если коэффициент нагрузки велик и некоторые ключи с большей вероятностью выпадут, чем другие, то переставьте цепь с помощью эвристика перехода на передний план может быть эффективным. Более сложные структуры данных, такие как сбалансированные деревья поиска, заслуживают рассмотрения только в том случае, если коэффициент загрузки велик (около 10 или более), или если распределение хэшей, вероятно, будет очень неравномерным, или если нужно даже гарантировать хорошую производительность. в худшем случае. Однако в этих случаях использование более крупной таблицы и / или лучшей хеш-функции может быть даже более эффективным.^{[нужна цитата ]}

Связанные хеш-таблицы также наследуют недостатки связанных списков. При хранении небольших ключей и значений накладные расходы на пространство следующий указатель в каждой записи записи может иметь значение. Дополнительным недостатком является то, что при обходе связанного списка производительность кеша, делая кэш процессора неэффективным.

Отдельная цепочка с ячейками заголовка списка

Конфликт хеширования путем отдельного связывания с головными записями в массиве ведра.

Некоторые реализации цепочки хранят первую запись каждой цепочки в самом массиве слотов.^[4]Количество обходов указателя в большинстве случаев уменьшается на единицу. Цель состоит в том, чтобы повысить эффективность кеширования доступа к хеш-таблице.

Недостатком является то, что пустая корзина занимает то же место, что и корзина с одной записью. Для экономии места в таких хэш-таблицах часто бывает столько же слотов, сколько хранимых записей, а это означает, что многие слоты имеют две или более записей.^{[нужна цитата ]}

Отдельная цепочка с другими структурами

Вместо списка можно использовать любую другую структуру данных, поддерживающую необходимые операции. Например, используя самобалансирующееся двоичное дерево поиска, теоретическое наихудшее время общих операций с хеш-таблицей (вставка, удаление, поиск) может быть уменьшено до O (журнал п) а не O (п). Однако это вносит дополнительную сложность в реализацию и может привести к еще худшей производительности для небольших хеш-таблиц, где время, затрачиваемое на вставку и балансировку дерева, больше, чем время, необходимое для выполнения линейный поиск на всех элементах списка.^[3][12] Реальным примером хэш-таблицы, в которой используется самобалансирующееся двоичное дерево поиска для сегментов, является HashMap класс в Ява версия 8.^[13]

Вариант называется хеш-таблица массива использует динамический массив для хранения всех записей, которые хешируются в одном слоте.^[14][15][16] Каждая вновь вставленная запись добавляется в конец динамического массива, назначенного слоту. Размер динамического массива изменяется в точно подогнанный Таким образом, он увеличивается только на необходимое количество байтов. Альтернативные методы, такие как увеличение массива по размеру блока или страницы было обнаружено, что они улучшают производительность вставки, но за счет экономии места. Этот вариант позволяет более эффективно использовать Кеширование ЦП и резервный буфер перевода (TLB), поскольку записи слотов хранятся в последовательных позициях памяти. Это также обходится без следующий указатели, необходимые для связанных списков, что экономит место. Несмотря на частое изменение размера массива, накладные расходы на пространство, понесенные операционной системой, такие как фрагментация памяти, оказались небольшими.^{[нужна цитата ]}

Развитием этого подхода является так называемый динамическое идеальное хеширование,^[17] где ведро, содержащее k записи организованы в виде идеальной хеш-таблицы с k² слоты. Хотя он использует больше памяти (п² слоты для п записи, в худшем случае и п × k слоты в среднем случае), этот вариант гарантирует постоянное время поиска в худшем случае и низкое амортизированное время для вставки. дерево слияния для каждого ковша, с высокой вероятностью достигая постоянного времени для всех операций.^[18]

Открытая адресация

Основная статья: Открытая адресация

Коллизия хэша разрешена открытой адресацией с линейным зондированием (интервал = 1). Обратите внимание, что «Тед Бейкер» имеет уникальный хеш, но, тем не менее, столкнулся с «Сандрой Ди», которая ранее столкнулась с «Джоном Смитом».

В другой стратегии, называемой открытой адресацией, все записи записей хранятся в самом массиве корзины. Когда необходимо вставить новую запись, сегменты исследуются, начиная со слота для хеширования и заканчивая некоторым. последовательность зонда, пока не будет найден незанятый слот. При поиске записи сегменты сканируются в той же последовательности, пока не будет найдена целевая запись или не будет найден неиспользуемый слот массива, что указывает на отсутствие такого ключа в таблице.^[19] Название «открытая адресация» относится к тому факту, что местоположение («адрес») элемента не определяется его хеш-значением. (Этот метод также называется закрытое хеширование; его не следует путать с «открытым хешированием» или «закрытой адресацией», которые обычно означают отдельную цепочку.)

Хорошо известные последовательности зондов включают:

• Линейное зондирование, в котором интервал между зондами фиксирован (обычно 1). Из-за хорошего Кэш процессора Использование и высокая производительность этот алгоритм наиболее широко используется на современных компьютерных архитектурах в реализациях хэш-таблиц.^[20]
• Квадратичное зондирование, в котором интервал между зондами увеличивается путем добавления последовательных выходов квадратичного полинома к начальному значению, заданному исходным хеш-вычислением
• Двойное хеширование, в котором интервал между зондами вычисляется второй хеш-функцией

Недостатком всех этих схем открытой адресации является то, что количество сохраненных записей не может превышать количество слотов в массиве корзины. Фактически, даже с хорошими хэш-функциями их производительность резко ухудшается, когда коэффициент загрузки превышает 0,7 или около того. Для многих приложений эти ограничения требуют использования динамического изменения размера с соответствующими затратами.^{[нужна цитата ]}

Схемы открытой адресации также предъявляют более строгие требования к хэш-функции: помимо более равномерного распределения ключей по сегментам, функция также должна минимизировать кластеризацию хеш-значений, которые идут последовательно в порядке проверки. Единственная проблема, связанная с раздельной цепочкой, заключается в том, что слишком много объектов сопоставляются с одно и тоже хеш-значение; находятся ли они рядом или рядом - совершенно неважно.^{[нужна цитата ]}

Открытая адресация экономит память только в том случае, если записи малы (меньше четырехкратного размера указателя) и коэффициент загрузки не слишком мал. Если коэффициент загрузки близок к нулю (т. Е. Сегментов гораздо больше, чем хранимых записей), открытая адресация будет расточительной, даже если каждая запись всего два. слова.

На этом графике сравнивается среднее количество промахов в кэше ЦП, необходимых для поиска элементов в больших хэш-таблицах (намного превышающих размер кеша) с цепочкой и линейным зондированием. Линейное зондирование работает лучше благодаря лучшему местонахождение ссылки, хотя при заполнении таблицы ее производительность резко ухудшается.

Открытая адресация позволяет избежать временных затрат на выделение каждой новой записи записи и может быть реализована даже при отсутствии распределителя памяти. Это также позволяет избежать дополнительного косвенного обращения, необходимого для доступа к первой записи каждой корзины (то есть, как правило, единственной). Он также лучше местонахождение ссылки, особенно с линейным зондированием. При небольших размерах записи эти факторы могут дать лучшую производительность, чем цепочка, особенно при поиске. Хеш-таблицы с открытой адресацией также проще сериализовать, потому что они не используют указатели.^{[нужна цитата ]}

С другой стороны, обычная открытая адресация - плохой выбор для больших элементов, потому что эти элементы заполняют весь Кэш процессора строк (что сводит на нет преимущество кеширования), и большое количество места тратится на большие пустые слоты таблицы. Если в открытой таблице адресации хранятся только ссылки на элементы (внешнее хранилище), она использует пространство, сопоставимое с цепочкой, даже для больших записей, но теряет преимущество в скорости.^{[нужна цитата ]}

Вообще говоря, открытую адресацию лучше использовать для хеш-таблиц с небольшими записями, которые могут храниться в таблице (внутреннее хранилище) и помещаться в строку кэша. Они особенно подходят для элементов одного слово или менее. Если ожидается, что таблица будет иметь высокий коэффициент загрузки, записи большие или данные имеют переменный размер, сцепленные хэш-таблицы часто работают так же или лучше.^{[нужна цитата ]}

Объединенное хеширование

Гибрид цепочки и открытой адресации, объединенное хеширование связывает вместе цепочки узлов внутри самой таблицы.^[19] Как и открытая адресация, она обеспечивает использование пространства и (несколько уменьшенные) преимущества кеширования по сравнению с цепочкой. Как и цепочка, он не проявляет эффектов кластеризации; Фактически, таблица может быть эффективно заполнена до высокой плотности. В отличие от цепочки, в нем не может быть больше элементов, чем слотов стола.

Кукушка хеширования

Еще одно альтернативное решение с открытой адресацией: кукушка, что обеспечивает постоянное время поиска и удаления в худшем случае и постоянное амортизированное время для вставок (с малой вероятностью, что произойдет худший случай). Он использует две или более хэш-функций, что означает, что любая пара ключ / значение может находиться в двух или более местах. Для поиска используется первая хеш-функция; если ключ / значение не найден, то используется вторая хеш-функция и так далее. Если во время вставки происходит коллизия, то ключ повторно хешируется с помощью второй хеш-функции, чтобы сопоставить его с другой корзиной. Если все хэш-функции используются и конфликт все еще существует, то ключ, с которым он столкнулся, удаляется, чтобы освободить место для нового ключа, а старый ключ повторно хешируется с одной из других хэш-функций, которая сопоставляет его с другой. ведро. Если это местоположение также приводит к конфликту, то процесс повторяется до тех пор, пока не исчезнет конфликт или процесс не пройдет все сегменты, после чего размер таблицы будет изменен. Комбинируя несколько хэш-функций с несколькими ячейками на ведро, можно достичь очень высокого использования пространства.^{[нужна цитата ]}

Хеширование в классическом стиле

Еще одно альтернативное решение с открытой адресацией: классическое хеширование,^[21] в котором сочетаются подходы кукушка и линейное зондирование, но в целом, кажется, избегает их ограничений. В частности, он хорошо работает, даже когда коэффициент загрузки превышает 0,9. Алгоритм хорошо подходит для реализации изменяемого размера параллельная хеш-таблица.

Алгоритм классического хеширования работает путем определения соседства сегментов рядом с исходным хешированным сегментом, где всегда находится данная запись. Таким образом, поиск ограничен числом записей в этой окрестности, которое в худшем случае является логарифмическим, в среднем - постоянным, а при правильном выравнивании окрестности обычно требуется один промах в кэше. При вставке записи сначала пытаются добавить ее в ведро по соседству. Однако, если все сегменты в этой окрестности заняты, алгоритм последовательно просматривает сегменты до тех пор, пока не будет найден открытый слот (незанятый сегмент) (как при линейном зондировании). В этот момент, поскольку пустое ведро находится за пределами соседства, элементы неоднократно перемещаются в последовательности переходов. (Это похоже на хеширование с кукушкой, но с той разницей, что в этом случае пустой слот перемещается по соседству, а не элементы, перемещаемые в надежде в конечном итоге найти пустой слот.) Каждый переход приближает открытый слот. в исходную окрестность, не аннулируя свойство соседства любого из ведер на этом пути. В конце концов, открытый слот был перемещен в соседство, и вставляемая запись может быть добавлена ​​к нему.^{[нужна цитата ]}

Робин Гуд хеширование

Вариантом разрешения конфликтов двойного хеширования является хеширование Робин Гуда.^[22][23] Идея состоит в том, что новый ключ может вытеснить уже вставленный ключ, если его счетчик проб больше, чем у ключа в текущей позиции. В итоге это сокращает время поиска в таблице в худшем случае. Это похоже на упорядоченные хеш-таблицы^[24] за исключением того, что критерий нажатия клавиши не зависит от прямой связи между клавишами. Поскольку и наихудший случай, и вариация в количестве зондов резко сокращаются, интересным вариантом является зондирование таблицы, начиная с ожидаемого успешного значения зондирования, а затем расширяется из этой позиции в обоих направлениях.^[25]Внешнее хеширование Робин Гуда является расширением этого алгоритма, в котором таблица хранится во внешнем файле, а каждая позиция таблицы соответствует странице или корзине фиксированного размера с B записи.^[26]

Хеширование с двумя вариантами

Хеширование с двумя вариантами использует две разные хэш-функции, час₁(Икс) и час₂(Икс) для хеш-таблицы. Обе хеш-функции используются для вычисления двух положений таблицы. Когда объект вставляется в таблицу, он помещается в то место таблицы, которое содержит меньше объектов (по умолчанию используется час₁(Икс) расположение таблицы при равенстве размеров ведра). Хеширование с двумя вариантами выбора использует принцип мощности двух вариантов.^[27]

Динамическое изменение размера

Когда вставка сделана так, что количество записей в хеш-таблице превышает произведение коэффициента загрузки и текущей емкости, тогда хеш-таблица должна быть перефразированный.^[9] Повторное хеширование включает увеличение размера базовой структуры данных^[9] и сопоставление существующих элементов с новыми местоположениями ведра. В некоторых реализациях, если начальная емкость больше, чем максимальное количество записей, деленное на коэффициент загрузки, никакие операции повторного хеширования никогда не будут выполняться.^[9]

Чтобы ограничить долю памяти, потраченной впустую из-за пустых корзин, некоторые реализации также уменьшают размер таблицы - с последующим повторным хешированием - при удалении элементов. С точки зрения компромисса между пространством и временем эта операция похожа на освобождение динамических массивов.

Изменение размера путем копирования всех записей

Распространенный подход - автоматически запускать полное изменение размера, когда коэффициент нагрузки превышает некоторый порог. р_{Максимум}. Тогда новая большая таблица выделенный, каждая запись удаляется из старой таблицы и вставляется в новую таблицу. Когда все записи удалены из старой таблицы, старая таблица возвращается в пул свободной памяти. Аналогичным образом, когда коэффициент нагрузки падает ниже второго порога р_мин, все записи перемещаются в новую меньшую таблицу.

Для хэш-таблиц, которые часто сжимаются и растут, уменьшение размера можно полностью пропустить. В этом случае размер таблицы пропорционален максимальному количеству записей, которые когда-либо были в хеш-таблице за один раз, а не текущему количеству. Недостатком является то, что использование памяти будет выше, и, следовательно, поведение кеша может быть хуже. Для лучшего контроля может быть предусмотрена операция «усадки до посадки», которая выполняется только по запросу.

Если размер таблицы увеличивается или уменьшается на фиксированный процент при каждом расширении, общая стоимость этих изменений размера, амортизированный по всем операциям вставки и удаления, остается константой, независимо от количества записей п и числа м выполненных операций.

Например, рассмотрим таблицу, которая была создана с минимально возможным размером и удваивается каждый раз, когда коэффициент загрузки превышает некоторый порог. Если м элементы вставляются в эту таблицу, общее количество дополнительных повторных вставок, которые происходят при всех динамических изменениях размера таблицы, не превышает м - 1. Другими словами, динамическое изменение размера примерно вдвое увеличивает стоимость каждой операции вставки или удаления.

Альтернативы перефразированию "все и сразу"

Некоторые реализации хеш-таблиц, особенно в системы реального времени, не может заплатить цену за увеличение хэш-таблицы сразу, потому что это может прервать критичные по времени операции. Если невозможно избежать динамического изменения размера, решение заключается в постепенном изменении размера.

Хеш-таблицы на основе диска почти всегда используют некоторую альтернативу повторному хешированию «все сразу», поскольку стоимость восстановления всей таблицы на диске будет слишком высокой.

Постепенное изменение размера

Альтернативой одновременному увеличению таблицы является постепенное перефразирование:

• Во время изменения размера выделите новую хеш-таблицу, но оставьте старую без изменений.
• При каждой операции поиска или удаления проверяйте обе таблицы.
• Выполняйте операции вставки только в новую таблицу.
• При каждой вставке также перемещайте р элементы из старой таблицы в новую таблицу.
• Когда все элементы будут удалены из старой таблицы, освободите ее.

Чтобы обеспечить полное копирование старой таблицы до того, как потребуется увеличить новую таблицу, необходимо увеличить размер таблицы как минимум в (р + 1)/р во время изменения размера.

Монотонные клавиши

Если известно, что ключи будут храниться в монотонно возрастающий (или убывающий) порядок, то вариация последовательное хеширование может быть достигнут.

Учитывая некоторый начальный ключ k₁, последующий ключ k_я перегородки ключевой домен [k₁, ∞) в набор {[k₁, k_я), [k_я, ∞)}. В общем, повторение этого процесса дает более тонкое разделение {[k₁, k_я0), [k_я0, k_я1), ..., [k_{яп - 1}, k_яп), [k_яп, ∞)} для некоторой последовательности монотонно возрастающих ключей (k_я0, ..., k_яп), куда п это количество уточнения. Применяется тот же процесс, mutatis mutandis, монотонно убывающим ключам. Назначив каждому подынтервал Для этого раздела используется другая хеш-функция или хеш-таблица (или и то, и другое), и за счет уточнения раздела всякий раз, когда размер хеш-таблицы изменяется, этот подход гарантирует, что хэш любого ключа, однажды выданный, никогда не изменится, даже если хеш-таблица будет увеличена.

Поскольку общее количество записей обычно увеличивается вдвое, будет только O (журнал (N)) подинтервалы для проверки, и время двоичного поиска для перенаправления будет O (log (log (N))).

Линейное хеширование

Линейное хеширование^[28] представляет собой алгоритм хеш-таблицы, который разрешает инкрементное расширение хеш-таблицы. Он реализован с использованием одной хэш-таблицы, но с двумя возможными функциями поиска.

Хеширование для распределенных хеш-таблиц

Другой способ снизить стоимость изменения размера таблицы - выбрать хеш-функцию таким образом, чтобы хеш-значения большинства значений не изменялись при изменении размера таблицы. Такие хеш-функции распространены в дисковых и распределенные хеш-таблицы, где повторное хеширование является непомерно дорогостоящим. Проблема разработки хеша, при котором большинство значений не изменяется при изменении размера таблицы, известна как распределенная хеш-таблица Проблема. Четыре наиболее популярных подхода: рандеву хеширование, последовательное хеширование, то сеть с адресацией по содержанию алгоритм, и Кадемлия расстояние.

Спектакль

Анализ скорости

В простейшей модели хэш-функция полностью не указана, и размер таблицы не изменяется. С идеальной хеш-функцией таблица размеров ${displaystyle k}$ с открытой адресацией не имеет коллизий и выдерживает до ${displaystyle k}$ элементы с одним сравнением для успешного поиска, а таблица размеров ${displaystyle k}$ с цепочкой и ${displaystyle n}$ ключи имеет минимум ${displaystyle max(0,n-k)}$ столкновения и ${displaystyle Theta (1+{frac {n}{k}})}$ сравнения для поиска. При наихудшей хэш-функции каждая вставка вызывает коллизию, и хеш-таблицы вырождают в линейный поиск, причем ${displaystyle Theta (n)}$ амортизированных сравнений на каждую вставку и до ${displaystyle n}$ сравнения для успешного поиска.

Добавить в эту модель перехеширование несложно. Как в динамический массив, геометрическое изменение размера в раз ${displaystyle b}$ подразумевает, что только ${displaystyle {frac {n}{b^{i}}}}$ ключи вставлены ${displaystyle i}$ или более раз, так что общее количество вставок ограничено сверху ${displaystyle {frac {bn}{b-1}}}$, который ${displaystyle Theta (n)}$. Используя повторное хеширование для поддержания ${displaystyle n<k}$таблицы, использующие как цепочку, так и открытую адресацию, могут иметь неограниченное количество элементов и выполнять успешный поиск в одном сравнении для лучшего выбора хэш-функции.

В более реалистичных моделях хеш-функция представляет собой случайная переменная по распределению вероятностей хэш-функций, а производительность вычисляется в среднем по выбору хэш-функции. Когда это распределение униформа, предположение называется "простым равномерным хешированием", и можно показать, что хеширование с цепочкой требует ${displaystyle Theta (1+{frac {n}{k}})}$ сравнения в среднем для неудачного поиска, а хеширование с открытой адресацией требует ${displaystyle Theta left({frac {1}{1-n/k}}ight)}$.^[29] Обе эти границы постоянны, если мы сохраняем '${displaystyle {frac {n}{k}}<c}$ используя изменение размера таблицы, где ${displaystyle c}$ фиксированная константа меньше 1.

Два фактора существенно влияют на задержку операций с хеш-таблицей:^[30]

• Кеш отсутствует. С увеличением коэффициента загрузки производительность поиска и вставки хеш-таблиц может сильно снизиться из-за увеличения среднего количества недостающего кеша.
• Стоимость изменения размера. Изменение размера становится чрезвычайно трудоемкой задачей, когда хеш-таблицы становятся огромными.

В программах, чувствительных к задержкам, требуется, чтобы затраты времени на операции как в среднем, так и в наихудшем случае были небольшими, стабильными и даже предсказуемыми. Хэш-таблица K ^[31] разработан для общего сценария приложений с малой задержкой, с целью достижения стабильных по стоимости операций на растущей таблице огромных размеров.

Использование памяти

Иногда требуется минимизировать потребность в памяти для таблицы. Один из способов уменьшить использование памяти в методах связывания - исключить некоторые из указателей связывания или заменить их некоторой формой сокращенных указателей.

Другой метод был представлен Дональдом Кнутом.^{[нужна цитата ]} и называется частное. Для этого обсуждения предположим, что ключ или обратимо хешированная версия этого ключа является целым числом. м из {0, 1, 2, ..., M-1} и количество сегментов N. м делится на N произвести частное q и остаток р. Остаток р используется для выбора ковша; в ведре только частное q нужно хранить. Это спасает бревно₂(N) бит на элемент, что может быть очень важным в некоторых приложениях.

Quotienting легко работает с цепочкой хеш-таблиц или с простыми хеш-таблицами с кукушкой. Чтобы применить эту технику к обычным хеш-таблицам с открытой адресацией, Джон Дж. Клири представил метод^[32] где два бита (a девственник немного и изменять bit) включены в каждую корзину, чтобы разрешить исходный индекс корзины (р) для реконструкции.

В только что описанной схеме бревно₂(M / N) + 2 бита используются для хранения каждого ключа. Интересно отметить, что теоретический минимум хранилища будет бревно₂(M / N) + 1,4427 бит, где 1,4427 = бревно₂(е).

Функции

Преимущества

• Основное преимущество хэш-таблиц перед другими структурами данных таблиц - скорость. Это преимущество более очевидно, когда количество записей велико. Хеш-таблицы особенно эффективны, когда максимальное количество записей можно спрогнозировать заранее, чтобы массив сегментов можно было выделить один раз с оптимальным размером и никогда не изменять его размер.
• Если набор пар ключ-значение фиксирован и известен заранее (поэтому вставки и удаления не допускаются), можно уменьшить среднюю стоимость поиска путем тщательного выбора хэш-функции, размера таблицы корзины и внутренних структур данных. В частности, можно разработать хеш-функцию, которая не допускает конфликтов или даже идеальна. В этом случае ключи не нужно хранить в таблице.

Недостатки

• Хотя операции с хеш-таблицей в среднем занимают постоянное время, стоимость хорошей хеш-функции может быть значительно выше, чем внутренний цикл алгоритма поиска для последовательного списка или дерева поиска. Таким образом, хеш-таблицы неэффективны, когда количество записей очень мало. (Однако в некоторых случаях высокая стоимость вычисления хэш-функции может быть уменьшена путем сохранения хеш-значения вместе с ключом.)
• Для некоторых приложений обработки строк, таких как проверка орфографии, хеш-таблицы могут быть менее эффективными, чем пытается, конечные автоматы, или же Джуди массивы. Кроме того, если существует не слишком много возможных ключей для хранения - то есть, если каждый ключ может быть представлен достаточно небольшим количеством бит - тогда вместо хеш-таблицы можно использовать ключ непосредственно в качестве индекса в массиве. ценностей. Обратите внимание, что в этом случае нет коллизий.
• Записи, хранящиеся в хэш-таблице, можно эффективно перечислить (с постоянной стоимостью записи), но только в некотором псевдослучайном порядке. Следовательно, не существует эффективного способа найти запись, ключ которой ближайший к заданному ключу. Список всех п записи в определенном порядке обычно требуют отдельного этапа сортировки, стоимость которого пропорциональна log (п) за запись. Для сравнения, упорядоченные деревья поиска имеют стоимость поиска и вставки, пропорциональную log (п), но позволяют найти ближайший ключ примерно с такой же стоимостью, и упорядоченный перечисление всех записей с постоянной стоимостью записи. Однако LinkingHashMap может быть создан для создания хеш-таблицы с неслучайной последовательностью.^[33]
• Если ключи не сохранены (потому что хеш-функция не имеет конфликтов), может не быть простого способа перечислить ключи, которые присутствуют в таблице в любой данный момент.
• Хотя средний Стоимость одной операции постоянна и довольно мала, стоимость одной операции может быть довольно высокой. В частности, если хеш-таблица использует динамическое изменение размера, операция вставки или удаления может иногда занимать время, пропорциональное количеству записей. Это может быть серьезным недостатком для приложений реального времени или интерактивных приложений.
• Хеш-таблицы в целом показывают плохие местонахождение ссылки - то есть данные, к которым необходимо получить доступ, распределяются в памяти как бы случайным образом. Поскольку хеш-таблицы вызывают скачкообразные шаблоны доступа, это может вызвать кэш микропроцессора пропуски, которые вызывают длительные задержки. Компактные структуры данных, такие как массивы, поиск которых выполняется с помощью линейный поиск может быть быстрее, если стол относительно небольшой, а клавиши компактные. Оптимальная производительность варьируется от системы к системе.
• Хеш-таблицы становятся совершенно неэффективными при большом количестве конфликтов. Хотя чрезвычайно неравномерное распределение хешей крайне маловероятно, злонамеренный противник со знанием хэш-функции может предоставить информацию в хэш, который создает наихудшее поведение, вызывая чрезмерные коллизии, что приводит к очень низкой производительности, например, отказ в обслуживании.^[34][35][36] В критически важных приложениях можно использовать структуру данных с лучшими гарантиями наихудшего случая; тем не мение, универсальное хеширование —А рандомизированный алгоритм это не позволяет злоумышленнику предсказать, какие входные данные вызывают наихудшее поведение - может быть предпочтительнее.^[37] Хеш-функция, используемая хеш-таблицей в Linux таблица маршрутизации Кэш был изменен в Linux версии 2.4.2 в качестве меры противодействия таким атакам.^[38]

Использует

Ассоциативные массивы

Основная статья: Ассоциативный массив

Хеш-таблицы обычно используются для реализации многих типов таблиц в памяти. Они используются для реализации ассоциативные массивы (массивы с произвольными индексами струны или другие сложные объекты), особенно в интерпретированный языки программирования подобно Рубин, Python, и PHP.

При сохранении нового объекта в Multimap и возникает хэш-коллизия, мультиотображение безоговорочно сохраняет оба элемента.

При сохранении нового элемента в типичном ассоциативном массиве возникает конфликт хешей, но сами ключи отличаются, ассоциативный массив также сохраняет оба элемента. Однако, если ключ нового элемента точно совпадает с ключом старого элемента, ассоциативный массив обычно стирает старый элемент и перезаписывает его новым элементом, поэтому каждый элемент в таблице имеет уникальный ключ.

Индексирование базы данных

Хеш-таблицы также могут использоваться как диск структуры данных и индексы базы данных (например, в dbm ) несмотря на то что B-деревья более популярны в этих приложениях. В системах баз данных с несколькими узлами хеш-таблицы обычно используются для распределения строк между узлами, что снижает сетевой трафик для хеш присоединяется.

Кеши

Основная статья: Кэш (вычисления)

Хеш-таблицы могут использоваться для реализации тайники, вспомогательные таблицы данных, которые используются для ускорения доступа к данным, которые в основном хранятся на более медленных носителях. В этом приложении конфликты хэшей можно обрабатывать, отбрасывая одну из двух конфликтующих записей - обычно стирая старый элемент, который в настоящее время хранится в таблице, и перезаписывая его новым элементом, чтобы каждый элемент в таблице имел уникальное значение хеш-функции.

Наборы

Помимо восстановления записи с заданным ключом, многие реализации хэш-таблиц также могут определить, существует ли такая запись или нет.

Таким образом, эти структуры можно использовать для реализации установить структуру данных,^[39] который просто записывает, принадлежит ли данный ключ указанному набору ключей. В этом случае структуру можно упростить, исключив все части, которые имеют отношение к входным значениям. Хеширование можно использовать для реализации как статических, так и динамических наборов.

Представление объекта

Несколько динамических языков, например Perl, Python, JavaScript, Lua, и Рубин используйте хеш-таблицы для реализации объекты. В этом представлении ключи - это имена членов и методов объекта, а значения - указатели на соответствующий член или метод.

Уникальное представление данных

Основная статья: Интернирование строк

Некоторые программы могут использовать хеш-таблицы, чтобы избежать создания нескольких символьных строк с одинаковым содержимым. Для этого все строки, используемые программой, хранятся в одном струнный пул реализован в виде хеш-таблицы, которая проверяется всякий раз, когда должна быть создана новая строка. Этот метод был представлен в Лисп переводчики под именем хеширование, и может использоваться со многими другими типами данных (деревья выражения в системе символьной алгебры, записи в базе данных, файлы в файловой системе, двоичные диаграммы решений и т. д.).

Таблица транспонирования

Основная статья: Таблица транспонирования

А таблица транспонирования в сложную хеш-таблицу, в которой хранится информация о каждом найденном разделе.^[40]

Реализации

В языках программирования

Многие языки программирования предоставляют функции хеш-таблиц либо в виде встроенных ассоциативных массивов, либо в стандартной комплектации. библиотека модули. В C ++ 11, например, unordered_map class предоставляет хеш-таблицы для ключей и значений произвольного типа.

В Ява язык программирования (включая вариант, который используется на Android ) включает HashSet, HashMap, LinkedHashSet, и LinkedHashMap общий коллекции.^[41]

В PHP 5 и 7, движок Zend 2 и движок Zend 3 (соответственно) используют одну из хэш-функций из Дэниел Дж. Бернштейн для генерации хэш-значений, используемых при управлении отображениями указателей данных, хранящихся в хэш-таблице. В исходном коде PHP он помечен как DJBX33A (Дэниел Дж. Бернштейн, Times 33 с добавлением).

Python реализация встроенной хеш-таблицы в виде диктовать тип, а также Perl Тип хэша (%) используется внутри для реализации пространств имен, и поэтому необходимо уделять больше внимания безопасности, то есть атакам с коллизиями. Python наборы также используют внутренние хэши для быстрого поиска (хотя они хранят только ключи, а не значения).^[42] CPython 3.6+ использует вариант хэш-таблицы с упорядоченной вставкой, реализованный путем разделения хранилища значений на массив и наличия в ванильной хеш-таблице только набора индексов.^[43]

в .NET Framework, поддержка хэш-таблиц предоставляется через неуниверсальный Хеш-таблица и общий Словарь классы, в которых хранятся пары ключ-значение, и общий HashSet класс, в котором хранятся только значения.

В Рубин хеш-таблица использует модель открытой адресации, начиная с Ruby 2.4.^[44][45]

В Ржавчина стандартная библиотека, общий HashMap и HashSet структуры используют линейное зондирование с кражей ведра Робин Гуда.

ANSI Болтовня определяет классы Набор / IdentitySet и Словарь / IdentityDictionary. Все реализации Smalltalk предоставляют дополнительные (еще не стандартизированные) версии WeakSet, WeakKeyDictionary и WeakValueDictionary.

Tcl переменные массива представляют собой хеш-таблицы, а словари Tcl - неизменяемые значения на основе хешей. Функциональность также доступна как функции библиотеки C Tcl_InitHashTable и др. (для общих хеш-таблиц) и Tcl_NewDictObj et al. (для значений словаря). Производительность была оценена независимо как чрезвычайно конкурентоспособная.^[46]

В Язык Wolfram поддерживает хеш-таблицы с версии 10. Они реализованы под названием Ассоциация.

Common Lisp предоставляет хеш-таблица класс для эффективных отображений. Несмотря на свое название, языковой стандарт не требует фактического соблюдения каких-либо методов хеширования для реализаций.^[47]

История

Идея хеширования возникла независимо в разных местах. В январе 1953 г. Ханс Петер Лун написал внутренний меморандум IBM, в котором использовалось хеширование с цепочкой.^[48] Джин Амдал, Элейн М. МакГроу, Натаниэль Рочестер, и Артур Сэмюэл примерно в то же время реализовал программу, использующую хеширование. Открытая адресация с линейным зондированием (относительно простое пошаговое выполнение) приписывается Амдалу, но Ершов (в России) была такая же идея.^[48]

Смотрите также

• Алгоритм поиска строки Рабина – Карпа
• Стабильное хеширование
• Последовательное хеширование
• Расширяемое хеширование
• Ленивое удаление
• Хеширование Пирсона
• ФотоДНК
• Структура данных поиска
• Параллельная хеш-таблица
• Запись (информатика)

Связанные структуры данных

Есть несколько структур данных, которые используют хэш-функции, но не могут считаться частными случаями хеш-таблиц:

• Фильтр Блума структура данных с эффективным использованием памяти, предназначенная для приблизительного поиска в постоянное время; использует хеш-функцию (-ы) и может рассматриваться как приблизительная хеш-таблица.
• Распределенная хеш-таблица (DHT), гибкая динамическая таблица, распределенная по нескольким узлам сети.
• Отображенное дерево хеш-массива, а три структура, похожая на сопоставленное дерево массива, но где каждый ключ хешируется первым.

Рекомендации

1. Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2009). Введение в алгоритмы (3-е изд.). Массачусетский Институт Технологий. С. 253–280. ISBN  978-0-262-03384-8.
2. Чарльз Э. Лейзерсон, Амортизированные алгоритмы, удвоение таблицы, потенциальный метод В архиве 7 августа 2009 г. Wayback Machine Лекция 13, курс MIT 6.046J / 18.410J Введение в алгоритмы - осень 2005 г.
3. Кнут, Дональд (1998). Искусство программирования. 3: Сортировка и поиск (2-е изд.). Эддисон-Уэсли. С. 513–558. ISBN  978-0-201-89685-5.
4. Кормен, Томас Х.; Лейзерсон, Чарльз Э.; Ривест, Рональд Л.; Штейн, Клиффорд (2001). «Глава 11: Хеш-таблицы». Введение в алгоритмы (2-е изд.). MIT Press и McGraw-Hill. стр.221 –252. ISBN  978-0-262-53196-2.
5. "Реализация хэш-кода JDK HashMap". В архиве с оригинала 21 мая 2017 года.
6. Пирсон, Карл (1900). «По критерию, согласно которому данная система отклонений от вероятного в случае коррелированной системы переменных такова, что можно разумно предположить, что она возникла в результате случайной выборки». Философский журнал. Серия 5. 50 (302). С. 157–175. Дои:10.1080/14786440009463897.
7. Плэкетт, Робин (1983). «Карл Пирсон и тест хи-квадрат». International Statistical Review (Международный статистический институт (ISI)). 51 (1). С. 59–72. Дои:10.2307/1402731. JSTOR  1402731.
8. Ван, Томас (март 1997 г.). "Prime Double Hash Table". Архивировано из оригинал 3 сентября 1999 г.. Получено 10 мая, 2015.
9. Документация Javadoc для HashMap в Java 10 https://docs.oracle.com/javase/10/docs/api/java/util/HashMap.html
10. «Хеш-таблица CS». allcomputerscience.com.
11. Жако Гельденхейс; Антти Валмари. «Структура данных, почти оптимальная для памяти». Цифровая библиотека ACM.
12. Пробст, Марк (30 апреля 2010 г.). "Линейный поиск против двоичного". В архиве с оригинала от 20 ноября 2016 г.. Получено 20 ноября, 2016.
13. «Как работает HashMap в JAVA». coding-geek.com. В архиве с оригинала от 19 ноября 2016 г.
14. Аскитис, Николай; Зобель, Джастин (октябрь 2005 г.). Разрешение конфликтов с учетом кеширования в хэш-таблицах строк. Труды 12-й Международной конференции «Обработка строк и поиск информации» (SPIRE 2005). 3772/2005. С. 91–102. Дои:10.1007/11575832_11. ISBN  978-3-540-29740-6.
15. Аскитис, Николай; Синха, Ранджан (2010). «Проектирование масштабируемых, эффективных кеш-памяти и попыток для строк». Журнал VLDB. 17 (5): 633–660. Дои:10.1007 / s00778-010-0183-9. ISSN  1066-8888. S2CID  432572.
16. Аскитис, Николай (2009). Быстрые и компактные хеш-таблицы для целочисленных ключей (PDF). Материалы 32-й Австралазийской конференции по компьютерным наукам (ACSC 2009). 91. С. 113–122. ISBN  978-1-920682-72-9. Архивировано из оригинал (PDF) 16 февраля 2011 г.. Получено 13 июня, 2010.
17. Эрик Демейн, Джефф Линд. 6.897: Расширенные структуры данных. Лаборатория компьютерных наук и искусственного интеллекта Массачусетского технологического института. Весна 2003 г. «Архивная копия» (PDF). В архиве (PDF) с оригинала 15 июня 2010 г.. Получено 30 июня, 2008.
18. Уиллард, Дэн Э. (2000). «Изучение вычислительной геометрии, деревьев Ван Эмде Боаса и хеширования с точки зрения дерева слияния». SIAM Журнал по вычислениям. 29 (3): 1030–1049. Дои:10.1137 / S0097539797322425. МИСТЕР  1740562..
19. Тененбаум, Аарон М .; Лангсам, Едидья; Огенштейн, Моше Дж. (1990). Структуры данных с использованием C. Прентис Холл. С. 456–461, с. 472. ISBN  978-0-13-199746-2.
20. Паг, Расмус; Родлер, Флемминг Фриче (2001). «Кукушка хеширования». Алгоритмы - ESA 2001. Конспект лекций по информатике. 2161. С. 121–133. CiteSeerX  10.1.1.25.4189. Дои:10.1007/3-540-44676-1_10. ISBN  978-3-540-42493-2.
21. Херлихи, Морис; Шавит, Нир; Цафрир, Моран (2008). «Хеширование в классиках». DISC '08: Материалы 22-го международного симпозиума по распределенным вычислениям. Берлин, Гейдельберг: Springer-Verlag. С. 350–364. CiteSeerX  10.1.1.296.8742.
22. Селис, Педро (1986). Робин Гуд хеширование (PDF) (Технический отчет). Департамент компьютерных наук, Университет Ватерлоо. CS-86-14. В архиве (PDF) из оригинала 17 июля 2014 г.
23. Гуссарт, Эммануэль (2013). «Робин Гуд хеширование». В архиве из оригинала 21 марта 2014 г.
24. Эмбл, Оле; Кнут, Дон (1974). «Упорядоченные хеш-таблицы». Компьютерный журнал. 17 (2): 135. Дои:10.1093 / comjnl / 17.2.135.
25. Виола, Альфредо (октябрь 2005 г.). «Точное распределение индивидуальных смещений при линейном хешировании с зондированием». Транзакции по алгоритмам (TALG). 1 (2): 214–242. Дои:10.1145/1103963.1103965. S2CID  11183559.
26. Селис, Педро (Март 1988 г.). Внешнее хеширование Робин Гуда (Технический отчет). Департамент компьютерных наук, Университет Индианы. TR246.
27. Митценмахер, Майкл; Richa, Andréa W .; Ситараман, Рамеш (2001). «Сила двух случайных выборов: обзор методов и результатов» (PDF). Гарвардский университет. В архиве (PDF) с оригинала 25 марта 2015 г.. Получено 10 апреля, 2015.
28. Литвин, Витольд (1980). «Линейное хеширование: новый инструмент для адресации файлов и таблиц». Proc. 6-я конференция по очень большим базам данных. С. 212–223.
29. Дуг Данэм. Лекционные заметки CS 4521 В архиве 22 июля 2009 г. Wayback Machine. Университет Миннесоты Дулут. Теоремы 11.2, 11.6. Последнее изменение 21 апреля 2009 г.
30. Энди Ке. Внутри задержки операций с хеш-таблицей Последнее изменение 30 декабря 2019 г.
31. Энди Ке. Хэш-таблица K, дизайн для приложений с малой задержкой Последнее изменение 20 декабря 2019 г.
32. Клерри (1984). «Компактные хэш-таблицы с использованием двунаправленного линейного измерения». Транзакции IEEE на компьютерах (9): 828–834. Дои:10.1109 / TC.1984.1676499. S2CID  195908955.
33. «LinkedHashMap (Java Platform SE 7)». docs.oracle.com. Получено 1 мая, 2020.
34. Александр Клинк и Юлиан Вельде Эффективные атаки отказа в обслуживании на платформы веб-приложений В архиве 16 сентября 2016 г. Wayback Machine, 28 декабря 2011 г., 28-й Конгресс коммуникаций Хаоса. Берлин, Германия.
35. Майк Леннон«Уязвимость хеш-таблицы делает возможными широкомасштабные DDoS-атаки» В архиве 19 сентября 2016 г. Wayback Machine.2011.
36. «Укрепление хеш-функции Perl». 6 ноября 2013 г. В архиве из оригинала 16 сентября 2016 г.
37. Кросби и Уоллах.Отказ в обслуживании с помощью атак с алгоритмической сложностью В архиве 4 марта 2016 г. Wayback Machine.quote: «современные универсальные методы хеширования могут дать производительность, сравнимую с обычными хэш-функциями, при этом будучи доказуемо защищенными от этих атак». «Универсальные хеш-функции ... являются ... решением, подходящим для враждебных сред ... в производственных системах. "
38. Бар-Йосеф, Ноа; Шерсть, Авишай (2007). Удаленные атаки алгоритмической сложности на рандомизированные хэш-таблицы Proc. Международная конференция по безопасности и криптографии (SECRYPT) (PDF). п. 124. В архиве (PDF) из оригинала от 16 сентября 2014 г.
39. «Установить (Java Platform SE 7)». docs.oracle.com. Получено 1 мая, 2020.
40. "Таблица транспозиции - вики по шахматному программированию". Chessprogramming.org. Получено 1 мая, 2020.
41. "Урок: Реализации (Учебники Java ™> Коллекции)". docs.oracle.com. В архиве с оригинала 18 января 2017 г.. Получено 27 апреля, 2018.
42. "Python: List vs Dict для поисковой таблицы". stackoverflow.com. В архиве с оригинала 2 декабря 2017 г.. Получено 27 апреля, 2018.
43. Димитрис Фасаракис Хиллиард. "Словари заказаны в Python 3.6+?". Переполнение стека.
44. Дмитрий Васин (19 июня 2018). «Знаете ли вы, как работает хеш-таблица? (Примеры на Ruby)». anadea.info. Получено 3 июля, 2019.
45. Джонан Шеффлер (25 декабря 2016 г.). «Выпущен Ruby 2.4: более быстрые хэши, унифицированные целые числа и лучшее округление». heroku.com. Получено 3 июля, 2019.
46. Крыло, Эрик. «Выбор хеш-таблицы 2: Восстание машин-переводчиков». LuaHashMap: простая в использовании библиотека хеш-таблиц для C. Программное обеспечение PlayControl. Архивировано из оригинал 14 октября 2013 г.. Получено 24 октября, 2019. Tcl победил? В любом случае эти тесты показали, что эти реализации интерпретатора имеют очень хорошие реализации хеширования и конкурируют с нашим эталонным тестом STL unordered_map. В частности, в случае Tcl и Lua они были чрезвычайно конкурентоспособными и часто находились в пределах 5% -10% от unordered_map, когда они не превосходили его. (24.10.2019 на исходном сайте все еще есть текст, но цифры выглядят сломанными, тогда как в архиве они нетронуты.)
47. "CLHS: ХЭШ-ТАБЛИЦА системного класса". lispworks.com/documentation/HyperSpec/Front/index.htm. В архиве с оригинала 22 октября 2019 г.. Получено 18 мая, 2020.
48. Mehta, Dinesh P .; Сахни, Сартадж (28 октября 2004 г.). Справочник по структурам данных и приложениям. п. 9-15. ISBN  978-1-58488-435-4.

дальнейшее чтение

• Тамассия, Роберто; Гудрич, Майкл Т. (2006). «Глава девятая: Карты и словари». Структуры данных и алгоритмы в Java: [обновлено для Java 5.0] (4-е изд.). Хобокен, Нью-Джерси: Уайли. стр.369 –418. ISBN  978-0-471-73884-8.
• McKenzie, B.J .; Harries, R .; Белл, Т. (февраль 1990 г.). «Выбор алгоритма хеширования». Практика и опыт работы с программным обеспечением. 20 (2): 209–224. Дои:10.1002 / spe.4380200207. HDL:10092/9691.

внешняя ссылка

• Хеш-функция для поиска в хеш-таблице пользователя Боб Дженкинс.
• Хеш-функции от Пола Хси
• Дизайн компактных и эффективных хеш-таблиц для Java
• NIST вход на хеш-таблицы
• Лекция о хэш-таблицах из Стэнфордского CS106A
• Структуры открытых данных - Глава 5 - Хеш-таблицы, Пэт Морин
• Введение в алгоритмы MIT: хеширование 1 Видео лекции MIT OCW
• Введение в алгоритмы MIT: хеширование 2 Видео лекции MIT OCW