Проблема дня рождения - Birthday problem

О годовых изменениях показателей смертности см. эффект дня рождения. Для математической головоломки, которую задавали на математической олимпиаде, см. День Рождения Шерил.

Вычисленная вероятность того, что по крайней мере два человека разделяют день рождения, по сравнению с количеством людей.

В теория вероятности, то проблема дня рождения или парадокс дня рождения касается вероятность что в наборе п случайно выбранных людей, у некоторых из них будет такой же день рождения. Посредством принцип голубятни, вероятность достигает 100%, когда количество людей достигает 367 (поскольку существует всего 366 возможных дней рождения, включая 29 февраля ). Однако вероятность 99,9% достигается всего с 70 людьми, а вероятность 50% - с 23 людьми. Эти выводы основаны на предположении, что каждый день в году (кроме 29 февраля) одинаково вероятен для дня рождения.

Фактические записи о рождении показывают, что в разные дни рождается разное количество людей. В этом случае можно показать, что количество людей, необходимое для достижения 50% -ного порога, составляет 23 человека. или меньше.^[1] Например, если половина людей родилась в один день, а другая половина - в другой, то любой два у людей будет 50% шанс разделить день рождения.

Может показаться удивительным, что группа всего из 23 человек требуется для достижения 50% вероятности того, что по крайней мере два человека в группе имеют один и тот же день рождения: этот результат, возможно, будет более правдоподобным, если учесть, что сравнение дней рождения действительно будет между каждой возможной парой индивидуумов = 23 × 22/2 = 253 сравнений, что намного больше половины количества дней в году (не более 183), в отличие от одного человека и сравнения его или ее дня рождения с все остальные. Проблема дня рождения не в "парадокс "в буквальном логическом смысле противоречиво, но на первый взгляд просто не интуитивно понятно.

Реальные приложения для решения проблемы дня рождения включают криптографическую атаку, называемую атака на день рождения, который использует эту вероятностную модель, чтобы уменьшить сложность нахождения столкновение для хэш-функция, а также вычисление приблизительного риска столкновения хэшей, существующего в хэшах заданного размера совокупности.

История проблемы неясна. Результат был приписан Гарольд Давенпорт;^[2] однако версия того, что сегодня считается проблемой дня рождения, была предложена ранее Рихард фон Мизес.^[3]

Расчет вероятности

Проблема состоит в том, чтобы вычислить приблизительную вероятность того, что в группе п люди по крайней мере двое имеют одинаковый день рождения. Для простоты варианты распределения, такие как високосные годы, двойняшки, сезонные колебания или вариации дня недели не принимаются во внимание, и предполагается, что все 365 возможных дней рождения одинаково вероятны. (Распределение дней рождения в реальной жизни не является равномерным, поскольку не все даты одинаково вероятны, но эти отклонения мало влияют на анализ.^{[nb 1]} Собственно, равномерное распределение дат рождения - худший случай.^[5])

Цель состоит в том, чтобы вычислить п(А), вероятность того, что по крайней мере два человека в комнате имеют одинаковый день рождения. Однако проще вычислить п(А′), вероятность того, что у двух человек в комнате нет одного дня рождения. Тогда, потому что А и А′ единственные две возможности, а также взаимоисключающий, п(А) = 1 − п(А′).

Из уважения к широко опубликованным решениям^{[который? ]} придя к выводу, что 23 - это минимальное количество людей, необходимое для п(А) что больше 50%, следующий расчет п(А) буду использовать 23 человека в качестве примера. Если пронумеровать 23 человека от 1 до 23, то мероприятие то, что у всех 23 человек разные дни рождения, это то же самое, что случай, когда у человека 2 не тот же день рождения, что у человека 1, и у этого человека 3 не тот же день рождения, что у человека 1 или человека 2, и так далее, и, наконец, этот человек 23 не имеет того же дня рождения, что и любой из лиц с 1 по 22. Пусть эти события соответственно будут называться «Событие 2», «Событие 3» и так далее. Можно также добавить «Событие 1», соответствующее событию дня рождения человека 1, которое происходит с вероятностью 1. Это сочетание событий может быть вычислено с использованием условная возможность: вероятность События 2 составляет 364/365, поскольку у человека 2 может быть любой день рождения, кроме дня рождения человека 1. Точно так же вероятность События 3 с учетом того, что Событие 2 произошло, составляет 363/365, так как человек 3 может иметь любой из дни рождения, которые еще не зарегистрированы лицами 1 и 2. Это продолжается до тех пор, пока, наконец, вероятность события 23, учитывая, что все предшествующие события произошли, составляет 343/365. Наконец, принцип условной вероятности подразумевает, что п(А′) равна произведению этих индивидуальных вероятностей:

${\displaystyle P(A')={\frac {365}{365}}\times {\frac {364}{365}}\times {\frac {363}{365}}\times {\frac {362}{365}}\times \cdots \times {\frac {343}{365}}}$

(1)

Члены уравнения (1) можно собрать, чтобы получить:

${\displaystyle P(A')=\left({\frac {1}{365}}\right)^{23}\times (365\times 364\times 363\times \cdots \times 343)}$

(2)

Вычисляя уравнение (2) дает п(А′) ≈ 0.492703

Следовательно, п(А) ≈ 1 − 0.492703 = 0.507297 (50.7297%).

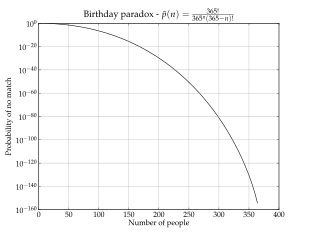
Этот процесс можно обобщить на группу п люди, где п(п) вероятность как минимум двух из п люди, разделяющие день рождения. Проще сначала рассчитать вероятность п(п) это все п дни рождения другой. Согласно принцип голубятни, п(п) равно нулю, когда п > 365. Когда п ≤ 365:

${\displaystyle {\begin{aligned}{\bar {p}}(n)&=1\times \left(1-{\frac {1}{365}}\right)\times \left(1-{\frac {2}{365}}\right)\times \cdots \times \left(1-{\frac {n-1}{365}}\right)\\[6pt]&={\frac {365\times 364\times \cdots \times (365-n+1)}{365^{n}}}\\[6pt]&={\frac {365!}{365^{n}(365-n)!}}={\frac {n!\cdot {\binom {365}{n}}}{365^{n}}}={\frac {_{365}P_{n}}{365^{n}}}\end{aligned}}}$

где ! это факториал оператор (³⁶⁵
_п) это биномиальный коэффициент и _kп_р обозначает перестановка.

Уравнение выражает тот факт, что у первого человека нет никого, у кого есть день рождения, у второго человека не может быть того же дня рождения, что и у первого (364/365), у третьего не может быть того же дня рождения, что и у первых двух (363/365), и в целом пдень рождения не может совпадать с любым из п − 1 предшествующие дни рождения.

В мероприятие по крайней мере двух из п лиц, имеющих один день рождения дополнительный все п дни рождения разные. Следовательно, его вероятность п(п) является

${\displaystyle p(n)=1-{\bar {p}}(n).}$

В следующей таблице показана вероятность для некоторых других значений п (для этой таблицы наличие високосных лет игнорируется, и предполагается, что каждый день рождения является одинаково вероятным):

Вероятность того, что в группе из двух человек не бывает одного дня рождения. п люди. Обратите внимание, что вертикальная шкала логарифмическая (каждый шаг вниз - 10²⁰ раз реже).

п	п(п)
1	00.0%
5	02.7%
10	11.7%
20	41.1%
23	50.7%
30	70.6%
40	89.1%
50	97.0%
60	99.4%
70	99.9%
75	99.97%
100	99.99997%
200	99.9999999999999999999999999998%
300	(100 − 6×10^−80)%
350	(100 − 3×10^−129)%
365	(100 − 1.45×10^−155)%
≥ 366	100%

Високосные годы. Если мы заменим 366 на 365 в формуле для ${\displaystyle {\bar {p}}(n)}$аналогичный расчет показывает, что для високосных лет количество человек, необходимое для вероятности совпадения более 50%, также равно 23; вероятность совпадения в этом случае составляет 50,6%.

Приближения

Графики, показывающие приблизительную вероятность того, что по крайней мере два человека разделят день рождения (красный) и его дополнительное событие (синий)

График, показывающий точность приближения 1 − е^{−​п2⁄₇₃₀} (красный)

В Серия Тейлор расширение экспоненциальная функция (постоянная е ≈ 2.718281828)

${\displaystyle e^{x}=1+x+{\frac {x^{2}}{2!}}+\cdots }$

обеспечивает приближение первого порядка для е^Икс для ${\displaystyle |x|\ll 1}$:

${\displaystyle e^{x}\approx 1+x.}$

Чтобы применить это приближение к первому выражению, полученному для п(п), набор Икс = −а/365. Таким образом,

${\displaystyle e^{-a/365}\approx 1-{\frac {a}{365}}.}$

Затем замените а с неотрицательными целыми числами для каждого члена в формуле п(п) до тех пор а = п − 1, например, когда а = 1,

${\displaystyle e^{-1/365}\approx 1-{\frac {1}{365}}.}$

Первое выражение, полученное для п(п) можно аппроксимировать как

${\displaystyle {\begin{aligned}{\bar {p}}(n)&\approx 1\cdot e^{-1/365}\cdot e^{-2/365}\cdots e^{-(n-1)/365}\\[6pt]&=e^{-\left.{\big (}1+2+\,\cdots \,+(n-1){\big )}\right/365}\\[6pt]&=e^{-(n(n-1)/2)/365}=e^{-n(n-1)/730}.\end{aligned}}}$

Следовательно,

${\displaystyle p(n)=1-{\bar {p}}(n)\approx 1-e^{-n(n-1)/730}.}$

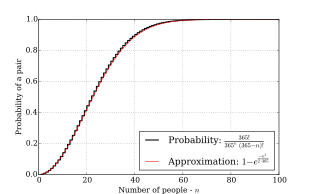
Еще более грубое приближение дается формулой

${\displaystyle p(n)\approx 1-e^{-n^{2}/730},}$

что, как показывает график, по-прежнему достаточно точное.

Согласно приближению, тот же подход можно применить к любому количеству «людей» и «дней». Если вместо 365 дней есть d, если есть п лиц, а если п ≪ d, то, используя тот же подход, что и выше, мы достигаем результата, что если п(п, d) это вероятность того, что по крайней мере два из п люди разделяют один и тот же день рождения из набора d доступные дни, затем:

${\displaystyle {\begin{aligned}p(n,d)&\approx 1-e^{-n(n-1)/(2d)}\\[6pt]&\approx 1-e^{-n^{2}/(2d)}.\end{aligned}}}$

Простое возведение в степень

Вероятность того, что у любых двух людей не один день рождения, равна 364/365. В комнате, содержащей п люди, есть (^п
₂) = п(п − 1)/2 пары людей, т.е. (^п
₂) События. Вероятность того, что у двух людей не будет один и тот же день рождения, можно приблизительно оценить, предположив, что эти события независимы, и, следовательно, умножив их вероятность вместе. Короче 364/365 можно умножить на себя (^п
₂) раз, что дает нам

${\displaystyle {\bar {p}}(n)\approx \left({\frac {364}{365}}\right)^{\binom {n}{2}}.}$

Так как это вероятность того, что ни у кого нет одного дня рождения, то вероятность того, что кто-то разделит день рождения, равна

${\displaystyle p(n)\approx 1-\left({\frac {364}{365}}\right)^{\binom {n}{2}}.}$

Пуассоновское приближение

Применяя Пуассон аппроксимация бинома на группу из 23 человек,

${\displaystyle \operatorname {Poi} \left({\frac {\binom {23}{2}}{365}}\right)=\operatorname {Poi} \left({\frac {253}{365}}\right)\approx \operatorname {Poi} (0.6932)}$

так

${\displaystyle \Pr(X>0)=1-\Pr(X=0)\approx 1-e^{-0.6932}\approx 1-0.499998=0.500002.}$

Результат более 50%, как и в предыдущих описаниях. Это приближение такое же, как и приведенное выше, основанное на разложении Тейлора, в котором используется ${\displaystyle e^{x}\approx 1+x}$.

Квадратное приближение

Хороший практическое правило который можно использовать для мысленный расчет это отношение

${\displaystyle p(n)\approx {\frac {n^{2}}{2m}}}$

который также можно записать как

${\displaystyle n\approx {\sqrt {2m\times p(n)}}}$

который хорошо работает для вероятностей, меньших или равных 1/2. В этих уравнениях м это количество дней в году.

Например, чтобы оценить количество людей, необходимое для 1/2 шанс общего дня рождения, мы получаем

${\displaystyle n\approx {\sqrt {2\times 365\times {\tfrac {1}{2}}}}={\sqrt {365}}\approx 19}$

Что не так уж далеко от правильного ответа 23.

Примерное количество человек

Это также можно приблизительно оценить, используя следующую формулу для количество людей необходимо иметь хотя бы 1/2 шанс совпадения:

${\displaystyle n\approx {\tfrac {1}{2}}+{\sqrt {{\tfrac {1}{4}}+2\times \ln(2)\times 365}}=22.999943.}$

Это результат хорошего приближения того, что событие с 1/k вероятность будет иметь 1/2 вероятность появления хотя бы один раз при повторении k пер. 2 раз.^[6]

Таблица вероятностей

Основная статья: Атака на день рождения

длина шестнадцатеричная строка	нет. из биты (б)	хеш-пространство размер (2б)	Количество хешированных элементов таких, что вероятность хотя бы одного хеш-коллизии ≥п
			п = 10^−18	п = 10^−15	п = 10^−12	п = 10^−9	п = 10^−6	п = 0.001	п = 0.01	п = 0.25	п = 0.50	п = 0.75
8	32	4.3×10^9	2	2	2	2.9	93	2.9×10^3	9.3×10^3	5.0×10^4	7.7×10^4	1.1×10^5
(10)	(40)	(1.1×10^12)	2	2	2	47	1.5×10^3	4.7×10^4	1.5×10^5	8.0×10^5	1.2×10^6	1.7×10^6
(12)	(48)	(2.8×10^14)	2	2	24	7.5×10^2	2.4×10^4	7.5×10^5	2.4×10^6	1.3×10^7	2.0×10^7	2.8×10^7
16	64	1.8×10^19	6.1	1.9×10^2	6.1×10^3	1.9×10^5	6.1×10^6	1.9×10^8	6.1×10^8	3.3×10^9	5.1×10^9	7.2×10^9
(24)	(96)	(7.9×10^28)	4.0×10^5	1.3×10^7	4.0×10^8	1.3×10^10	4.0×10^11	1.3×10^13	4.0×10^13	2.1×10^14	3.3×10^14	4.7×10^14
32	128	3.4×10^38	2.6×10^10	8.2×10^11	2.6×10^13	8.2×10^14	2.6×10^16	8.3×10^17	2.6×10^18	1.4×10^19	2.2×10^19	3.1×10^19
(48)	(192)	(6.3×10^57)	1.1×10^20	3.5×10^21	1.1×10^23	3.5×10^24	1.1×10^26	3.5×10^27	1.1×10^28	6.0×10^28	9.3×10^28	1.3×10^29
64	256	1.2×10^77	4.8×10^29	1.5×10^31	4.8×10^32	1.5×10^34	4.8×10^35	1.5×10^37	4.8×10^37	2.6×10^38	4.0×10^38	5.7×10^38
(96)	(384)	(3.9×10^115)	8.9×10^48	2.8×10^50	8.9×10^51	2.8×10^53	8.9×10^54	2.8×10^56	8.9×10^56	4.8×10^57	7.4×10^57	1.0×10^58
128	512	1.3×10^154	1.6×10^68	5.2×10^69	1.6×10^71	5.2×10^72	1.6×10^74	5.2×10^75	1.6×10^76	8.8×10^76	1.4×10^77	1.9×10^77

Более светлые поля в этой таблице показывают количество хешей, необходимых для достижения заданной вероятности коллизии (столбец) с учетом хеш-пространства определенного размера в битах (строка). Используя аналогию с днем ​​рождения: «размер хеш-пространства» похож на «доступные дни», «вероятность столкновения» похожа на «вероятность общего дня рождения», а «необходимое количество хешированных элементов» похоже на «требуемое количество людей в группа". Можно также использовать эту диаграмму для определения минимального требуемого размера хэша (с учетом верхних границ хешей и вероятности ошибки) или вероятности коллизии (для фиксированного количества хешей и вероятности ошибки).

Для сравнения, 10⁻¹⁸ к 10⁻¹⁵ - это уровень неисправимых битовых ошибок типичного жесткого диска.^[7] Теоретически 128-битные хеш-функции, такие как MD5, должен оставаться в этом диапазоне примерно до 8.2×10¹¹ документы, даже если его возможных выходов намного больше.

Верхняя граница вероятности и нижняя граница количества людей

Приведенный ниже аргумент адаптирован из аргумента Пол Халмос.^{[nb 2]}

Как указано выше, вероятность того, что никакие два дня рождения не совпадают, равна

${\displaystyle 1-p(n)={\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right).}$

Как и в предыдущих параграфах, интерес представляют самые маленькие п такой, что п(п) > 1/2; или, что то же самое, наименьшее п такой, что п(п) < 1/2.

Используя неравенство 1 − Икс < е^−Икс в приведенном выше выражении мы заменяем 1 − k/365 с участием е^{​−k⁄₃₆₅}. Это дает

${\displaystyle {\bar {p}}(n)=\prod _{k=1}^{n-1}\left(1-{\frac {k}{365}}\right)<\prod _{k=1}^{n-1}\left(e^{-k/365}\right)=e^{-n(n-1)/730}.}$

Поэтому приведенное выше выражение является не только приближением, но и верхняя граница из п(п). Неравенство

${\displaystyle e^{-n(n-1)/730}<{\frac {1}{2}}}$

подразумевает п(п) < 1/2. Решение для п дает

${\displaystyle n^{2}-n>730\ln 2.}$

Сейчас же, 730 лин 2 составляет приблизительно 505,997, что чуть ниже 506, значение п² − п достигнуто, когда п = 23. Следовательно, достаточно 23 человек. Кстати, решая п² − п = 730 лн 2 для п дает приближенную формулу Фрэнка Х. Мэтиса, процитированную выше.

Этот вывод показывает только, что в большинстве 23 человека нужны, чтобы обеспечить совпадение в день рождения с равными шансами; это оставляет возможность, что п 22 или меньше тоже может работать.

Обобщения

Обобщенная проблема дня рождения

Учитывая год с d дней, общая проблема дня рождения запрашивает минимальное количество п(d) так что в наборе п случайно выбранных людей, вероятность совпадения дня рождения не менее 50%. Другими словами, п(d) это минимальное целое число п такой, что

${\displaystyle 1-\left(1-{\frac {1}{d}}\right)\left(1-{\frac {2}{d}}\right)\cdots \left(1-{\frac {n-1}{d}}\right)\geq {\frac {1}{2}}.}$

Таким образом, классическая задача дня рождения соответствует определению п(365). Первые 99 значений п(d) приведены здесь (последовательность A033810 в OEIS ):

d	1–2	3–5	6–9	10–16	17–23	24–32	33–42	43–54	55–68	69–82	83–99
п(d)	2	3	4	5	6	7	8	9	10	11	12

Аналогичный расчет показывает, что п(d) = 23, когда d находится в диапазоне 341–372.

Ряд оценок и формул для п(d) были опубликованы.^[8]Для любого d ≥ 1, число п(d) удовлетворяет^[9]

${\displaystyle {\frac {3-2\ln 2}{6}}<n(d)-{\sqrt {2d\ln 2}}\leq 9-{\sqrt {86\ln 2}}.}$

Эти оценки оптимальны в том смысле, что последовательность п(d) − √2d пер. 2становится произвольно близко к

${\displaystyle {\frac {3-2\ln 2}{6}}\approx 0.27,}$

пока у него есть

${\displaystyle 9-{\sqrt {86\ln 2}}\approx 1.28}$

как максимум, взятый за d = 43.

Оценки достаточно жесткие, чтобы дать точное значение п(d) в 99% случаев, например п(365) = 23. В общем случае из этих оценок следует, что п(d) всегда равно либо

${\displaystyle \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil \quad {\text{or}}\quad \left\lceil {\sqrt {2d\ln 2}}\,\right\rceil +1}$

где ⌈ · ⌉ обозначает функция потолка.Формула

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}\,\right\rceil }$

выполняется для 73% всех целых чисел d.^[10] Формула

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}\right\rceil }$

держится для почти все d, т.е. для набора целых чисел d с участием асимптотическая плотность 1.^[10]

Формула

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}\right\rceil }$

относится ко всем d ≤ 10¹⁸, но предполагается, что контрпримеров к этой формуле бесконечно много.^[11]

Формула

${\displaystyle n(d)=\left\lceil {\sqrt {2d\ln 2}}+{\frac {3-2\ln 2}{6}}+{\frac {9-4(\ln 2)^{2}}{72{\sqrt {2d\ln 2}}}}-{\frac {2(\ln 2)^{2}}{135d}}\right\rceil }$

относится ко всем d ≤ 10¹⁸, и предполагается, что эта формула верна для всех d.^[11]

Более 2-х человек

Можно расширить задачу, задав вопрос, сколько человек в группе необходимо для того, чтобы с вероятностью более 50% было не менее 3/4/5 и т. Д. группы имеют один день рождения.

Первые несколько значений следующие:> 50% вероятность того, что 3 человека разделяют день рождения - 88 человек; > 50% вероятность того, что 4 человека разделят день рождения - 187 человек. Полный список можно найти как последовательность A014088 в Интернет-энциклопедии целочисленных последовательностей.^[12]

Cast как проблема столкновения

Задачу дня рождения можно обобщить следующим образом:

Данный п случайные целые числа, взятые из дискретное равномерное распределение с диапазоном [1,d], какова вероятность п(п; d) что как минимум два числа совпадают? (d = 365 дает обычную задачу дня рождения.)^[13]

Общие результаты могут быть получены с использованием тех же аргументов, которые приведены выше.

${\displaystyle {\begin{aligned}p(n;d)&={\begin{cases}1-\displaystyle \prod _{k=1}^{n-1}\left(1-{\frac {k}{d}}\right)&n\leq d\\1&n>d\end{cases}}\\[8px]&\approx 1-e^{-{\frac {n(n-1)}{2d}}}\\&\approx 1-\left({\frac {d-1}{d}}\right)^{\frac {n(n-1)}{2}}\end{aligned}}}$

Наоборот, если п(п; d) обозначает количество случайных целых чисел, взятых из [1,d] получить вероятность п что как минимум два числа совпадают, тогда

${\displaystyle n(p;d)\approx {\sqrt {2d\cdot \ln \left({\frac {1}{1-p}}\right)}}.}$

Проблема дня рождения в этом более общем смысле относится к хэш-функции: ожидаемое количество N-немного хэши, которые могут быть сгенерированы до столкновения, не 2^N, а скорее только 2^​N⁄₂. Это используется нападки на день рождения на криптографические хеш-функции и является причиной того, что небольшое количество столкновений в хеш-таблица для всех практических целей неизбежны.

Теория проблемы дня рождения была использована Зои Шнабель.^[14] под названием захват-повторный захват статистика для оценки численности рыбной популяции в озерах.

Обобщение на несколько типов

График вероятности хотя бы одного общего дня рождения хотя бы у одного мужчины и одной женщины

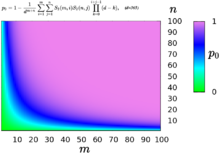
В основной задаче все испытания считаются однотипными. Задача дня рождения была обобщена для рассмотрения произвольного числа типов.^[15] В простейшем расширении есть два типа людей, скажем м мужчины и п женщины, и проблема становится характеристикой вероятности общего дня рождения хотя бы у одного мужчины и одной женщины. (Общие дни рождения двух мужчин или двух женщин не учитываются.) Вероятность отсутствия общих дней рождения здесь равна

${\displaystyle p_{0}={\frac {1}{d^{m+n}}}\sum _{i=1}^{m}\sum _{j=1}^{n}S_{2}(m,i)S_{2}(n,j)\prod _{k=0}^{i+j-1}d-k}$

где d = 365 и S₂ находятся Числа Стирлинга второго рода. Следовательно, искомая вероятность равна 1 − п₀.

Этот вариант задачи о дне рождения интересен тем, что не существует однозначного решения для общего количества людей. м + п. Например, обычное значение вероятности 50% реализуется как для группы из 32 человек, состоящей из 16 мужчин и 16 женщин, так и для группы из 49 человек, состоящей из 43 женщин и 6 мужчин.

Другие проблемы с днем ​​рождения

Первый матч

Связанный с этим вопрос: когда люди входят в комнату по одному, у кого из них, скорее всего, будет тот же день рождения, что и у кого-то, кто уже находится в комнате? То есть для чего п является п(п) − п(п − 1) максимум? Ответ - 20 - если есть приз за первый матч, лучшая позиция в очереди - 20-е.^{[нужна цитата ]}

В тот же день рождения, что и ты

Сравнение п(п) = вероятность совпадения дня рождения с q(п) = вероятность совпадения ваш день рождения

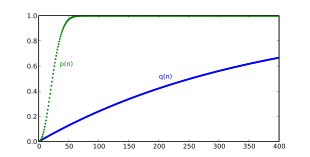
В задаче о дне рождения ни один из двух человек заранее не выбран. Напротив, вероятность q(п) что кто-то в комнате п у других людей тот же день рождения, что и у конкретный человек (например, вы) дается

${\displaystyle q(n)=1-\left({\frac {365-1}{365}}\right)^{n}}$

и для общего d от

${\displaystyle q(n;d)=1-\left({\frac {d-1}{d}}\right)^{n}.}$

В стандартном случае d = 365, заменяя п = 23 дает около 6,1%, что составляет менее 1 шанса из 16. С вероятностью более 50%, что один человек в комнате, заполненной п у людей такой же день рождения как ты, п должно быть не менее 253. Это число значительно выше, чем 365/2 = 182.5: причина в том, что, вероятно, есть совпадения в день рождения среди других людей в комнате.

Ближайшие матчи

Другое обобщение - спросить о вероятности нахождения хотя бы одной пары в группе п люди с днями рождения внутри k календарных дней друг друга, если есть d одинаково вероятны дни рождения.^[16]

${\displaystyle {\begin{aligned}p(n,k,d)&=1-{\frac {(d-nk-1)!}{d^{n-1}{\bigl (}d-n(k+1){\bigr )}!}}\end{aligned}}}$

Количество людей, необходимое для того, чтобы вероятность того, что у какой-то пары будет день рождения, разделена k дней или меньше будет выше 50%, как указано в следующей таблице:

k	п для d = 365
0	23
1	14
2	11
3	9
4	8
5	8
6	7
7	7

Таким образом, в группе из семи случайных людей более вероятно, что у двоих из них будет день рождения в пределах недели друг от друга.^[16]

Подсчет столкновений

Вероятность того, что kое целое число, случайно выбранное из [1,d] будет повторять хотя бы один предыдущий выбор равно q(k − 1; d) над. Ожидаемое общее количество раз, когда выбор будет повторять предыдущий выбор как п такие целые числа выбираются равными^[17]

${\displaystyle \sum _{k=1}^{n}q(k-1;d)=n-d+d\left({\frac {d-1}{d}}\right)^{n}.}$

Среднее количество человек

В альтернативной формулировке задачи о дне рождения задают вопрос: средний количество людей, необходимое для того, чтобы найти пару с одним днем ​​рождения. Если рассматривать функцию вероятности Pr [п у людей хотя бы один общий день рождения], это средний определяет значить распределения, в отличие от обычной формулировки, которая требует медиана. Проблема актуальна для нескольких алгоритмы хеширования проанализирован Дональд Кнут в его книге Искусство программирования. Это может быть показано^[18][19] что если взять единообразную выборку с заменой из большой популяции M, количество испытаний, необходимое для первого повторного отбора проб немного человек имеет ожидаемое значение п = 1 + Q(M), где

${\displaystyle Q(M)=\sum _{k=1}^{M}{\frac {M!}{(M-k)!M^{k}}}.}$

Функция

${\displaystyle Q(M)=1+{\frac {M-1}{M}}+{\frac {(M-1)(M-2)}{M^{2}}}+\cdots +{\frac {(M-1)(M-2)\cdots 1}{M^{M-1}}}}$

был изучен Шриниваса Рамануджан и имеет асимптотическое разложение:

${\displaystyle Q(M)\sim {\sqrt {\frac {\pi M}{2}}}-{\frac {1}{3}}+{\frac {1}{12}}{\sqrt {\frac {\pi }{2M}}}-{\frac {4}{135M}}+\cdots .}$

С участием M = 365 дней в году, среднее количество людей, необходимое для того, чтобы найти пару с одинаковым днем ​​рождения, составляет п = 1 + Q(M) ≈ 24.61659, несколько больше 23, число, необходимое для 50% вероятности. В лучшем случае хватит двух человек; в худшем случае максимально возможное количество M + 1 = 366 люди нужны; но в среднем требуется всего 25 человек

Анализ с использованием индикаторных случайных величин может дать более простой, но приблизительный анализ этой проблемы.^[20] Для каждой пары (i, j) на k человек в комнате определим индикаторную случайную величину X_ij, для ${\displaystyle 1\leq i\leq j\leq k}$, от

${\displaystyle {\begin{alignedat}{2}X_{ij}&=I\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}\\&={\begin{cases}1,&{\text{if person }}i{\text{ and person }}j{\text{ have the same birthday;}}\\0,&{\text{otherwise.}}\end{cases}}\end{alignedat}}}$

${\displaystyle {\begin{alignedat}{2}E[X_{ij}]&=\Pr\{{\text{person }}i{\text{ and person }}j{\text{ have the same birthday}}\}\\&=1/n\end{alignedat}}}$

Пусть X - случайная величина, считающая пары людей с одним днем ​​рождения.

${\displaystyle X=\sum _{i=1}^{k}\sum _{j=i+1}^{k}X_{ij}}$

${\displaystyle {\begin{alignedat}{3}E[X]&=\sum _{i=1}^{k}\sum _{j=i+1}^{k}E[X_{ij}]\\&={\binom {k}{2}}{\frac {1}{n}}\\&={\frac {k(k-1)}{2n}}\\\end{alignedat}}}$

Для п = 365, если k = 28, ожидаемое число с таким же днем ​​рождения равно ${\displaystyle (28\cdot 27)/(2\cdot 365)\approx 1.0356.}$ Таким образом, мы можем ожидать хотя бы одну подходящую пару, по крайней мере, из 28 человек.

Неформальную демонстрацию проблемы можно сделать из список премьер-министров Австралии, из которых на 2017 год - 29^{[Обновить]}, в котором Пол Китинг, 24-й премьер-министр, и Эдмунд Бартон У первого премьер-министра один день рождения, 18 января.

в 2014 Чемпионат мира по футболу, в каждом из 32 отрядов было по 23 игрока. Анализ официальных списков команд показал, что у 16 ​​команд были пары игроков, у которых были дни рождения, и из этих 5 команд было две пары: Аргентина, Франция, Иран, Южная Корея и Швейцария имели по две пары, а Австралия, Босния и Герцеговина, Бразилия. , Камерун, Колумбия, Гондурас, Нидерланды, Нигерия, Россия, Испания и США - каждая по одной паре.^[21]

Ворачек, Тран и Formann показали, что большинство людей заметно переоценивают количество людей, необходимое для достижения заданной вероятности того, что у людей будет один и тот же день рождения, и заметно недооценивают вероятность того, что люди будут иметь один и тот же день рождения, при заданном размере выборки.^[22] Дальнейшие результаты показали, что студенты-психологи и женщины справились с задачей лучше, чем посетители / персонал казино или мужчины, но были менее уверены в своих оценках.

Обратная задача

Обратная задача - найти для фиксированной вероятности п,величайший п для которого вероятность п(п) меньше заданного п, или самый маленький п для которого вероятность п(п) больше заданного п.^{[нужна цитата ]}

Принимая приведенную выше формулу для d = 365, надо

${\displaystyle n(p;365)\approx {\sqrt {730\ln \left({\frac {1}{1-p}}\right)}}.}$

В следующей таблице приведены некоторые примеры расчетов.

п	п	п↓	п(п↓)	п↑	п(п↑)
0.01	0.14178√365 = 2.70864	2	0.00274	3	0.00820
0.05	0.32029√365 = 6.11916	6	0.04046	7	0.05624
0.1	0.45904√365 = 8.77002	8	0.07434	9	0.09462
0.2	0.66805√365 = 12.76302	12	0.16702	13	0.19441
0.3	0.84460√365 = 16.13607	16	0.28360	17	0.31501
0.5	1.17741√365 = 22.49439	22	0.47570	23	0.50730
0.7	1.55176√365 = 29.64625	29	0.68097	30	0.70632
0.8	1.79412√365 = 34.27666	34	0.79532	35	0.81438
0.9	2.14597√365 = 40.99862	40	0.89123	41	0.90315
0.95	2.44775√365 = 46.76414	46	0.94825	47	0.95477
0.99	3.03485√365 = 57.98081	57	0.99012	58	0.99166

Некоторые значения, выходящие за границы, были цветной чтобы показать, что приближение не всегда точное.

Проблема с разделом

Связанная проблема - это проблема раздела, вариант проблема с рюкзаком из исследования операций. Некоторые веса ставятся на шкала баланса; каждый вес представляет собой целое число граммов, случайно выбранных от одного грамма до одного миллиона граммов (один тонна ). Вопрос в том, можно ли обычно (то есть с вероятностью, близкой к 1) переносить веса между левой и правой рукой, чтобы сбалансировать весы. (В случае, если сумма всех весов - нечетное количество граммов, допускается отклонение в один грамм.) Если есть только два или три веса, ответ, безусловно, отрицательный; хотя есть некоторые комбинации, которые работают, большинство случайно выбранных комбинаций трех весов не работают. Если весов очень много, ответ однозначно положительный. Вопрос в том, сколько всего достаточно? То есть, какое количество весов такое, что их можно будет уравновесить с равной вероятностью, поскольку это невозможно?

Часто интуиция подсказывает, что ответ выше. 100000. Интуиция большинства людей подсказывает, что их исчисляются тысячами или десятками тысяч, в то время как другие считают, что их должны быть как минимум сотни. Правильный ответ - 23.^{[нужна цитата ]}

Причина в том, что правильное сравнение заключается в количестве разделений весов на левую и правую. Есть 2^{N − 1} разные перегородки для N веса, а левую сумму за вычетом правой суммы можно рассматривать как новую случайную величину для каждого раздела. Распределение суммы весов приблизительно Гауссовский, с пиком на 1000000N и ширина 1000000√N, так что когда 2^{N − 1} примерно равно 1000000√N переход происходит. 2^{23 − 1} составляет около 4 миллионов, а ширина раздачи всего 5 миллионов.^[23]

В художественной литературе

Артур Кларк роман Падение лунной пыли, опубликованный в 1961 году, содержит раздел, в котором главные герои, оказавшиеся в ловушке под землей на неопределенное время, празднуют день рождения и обсуждают актуальность проблемы дня рождения. Как заявил пассажир-физик: «Если у вас группа из более чем двадцати четырех человек, шансы даже выше, чем даже у двоих из них в один день рождения». В конце концов, из 22 присутствующих выясняется, что у двух персонажей один день рождения, 23 мая.

Заметки

1. На самом деле дни рождения распределяются в течение года неравномерно; в одни сезоны рождается больше детей в день, чем в другие, но для решения этой проблемы распределение считается равномерным. В частности, многие дети рождаются летом, особенно в августе и сентябре (для северного полушария). [1], а в США было отмечено, что многие дети рождаются в праздничные дни Рождество и Новый год.^[1] Кроме того, потому что в больницах редко кесарево сечение и индуцированные роды в выходные дни между вторником и пятницей рождается больше людей, чем в выходные дни;^[1] когда у многих людей общий год рождения (например, в классе в школе), это создает тенденцию к определенным датам. В Швеции 9,3% населения рождается в марте и 7,3% в ноябре, когда равномерное распределение дает 8,3%. Шведский статистический совет. Смотрите также:
   • Мерфи, Рон. «Анализ распределения дней рождения в календарном году». Получено 2011-12-27.
   • Mathers, C D; Р. С. Харрис (1983). «Сезонное распределение рождений в Австралии». Международный журнал эпидемиологии. 12 (3): 326–331. Дои:10.1093 / ije / 12.3.326. PMID  6629621. Получено 2011-12-27.
   Эти факторы, как правило, увеличивают вероятность идентичных дат рождения, поскольку более плотное подмножество имеет больше возможных пар (в крайнем случае, когда все родились в три дня, очевидно, будет много одинаковых дней рождения). Проблема неравномерного количества рождений, происходящих в каждый день года, впервые была понята Мюррей Кламкин в 1967 г.^[4] Формальное доказательство того, что вероятность двух совпадающих дней рождения наименьшая для равномерного распределения дней рождения, было дано Блумом (Блум 1973 ).
2. В своей автобиографии Халмос раскритиковал форму, в которой часто изображается парадокс дня рождения, с точки зрения числовых вычислений. Он считал, что это следует использовать как пример использования более абстрактных математических понятий. Он написал:

   Рассуждения основаны на важных инструментах, к которым все студенты-математики должны иметь свободный доступ. Проблема дня рождения была великолепной иллюстрацией преимуществ чистого мышления перед механическими манипуляциями; неравенства могут быть получены за минуту или две, тогда как умножение займет гораздо больше времени и будет гораздо более подвержено ошибкам, независимо от того, является ли инструмент карандашом или старомодным настольным компьютером. Что калькуляторы не поддаются пониманию, математическим возможностям или прочной основе для более продвинутых обобщенных теорий.

использованная литература

1. Марио Кортина Борха; Джон Хей (сентябрь 2007 г.). «Проблема дня рождения». Значение. Королевское статистическое общество. 4 (3): 124–127. Дои:10.1111 / j.1740-9713.2007.00246.x.
2. У. В. Роуз Болл и H.S.M. Coxeter, "Mathematical Recreations and Essays, 13th edition", Dover Publications, New York, 1987, p 45.
3. Frank, P .; Goldstein, S .; Kac, M .; Prager, W .; Szegö, G .; Биркгоф, Г., ред. (1964). Избранные статьи Рихарда фон Мизеса. 2. Провиденс, Род-Айленд: амер. Математика. Soc. С. 313–334.
4. Кламкин и Ньюман 1967.
5. Стил, Дж. Майкл (2004). Мастер-класс Коши-Шварца. Кембридж: Издательство Кембриджского университета. стр.206, 277. ISBN  9780521546775.
6. Матис, Фрэнк Х. (июнь 1991 г.). «Общая проблема дня рождения». SIAM Обзор. 33 (2): 265–270. Дои:10.1137/1033051. ISSN  0036-1445. JSTOR  2031144. OCLC  37699182.
7. Джим Грей, Кэтрин ван Инген. Эмпирические измерения частоты отказов дисков и ошибок
8. Д. Бринк, (вероятно) точное решение проблемы дней рождения, Ramanujan Journal, 2012, [2].
9. Brink2012, Теорема 2
10. Brink2012, Теорема 3
11. Brink2012, Таблица 3, Гипотеза 1
12. «Минимальное количество людей, дающее 50% вероятность иметь хотя бы n совпадающих дней рождения в течение одного года». Он-лайн энциклопедия целочисленных последовательностей. OEIS. Получено 17 февраля 2020.
13. Сузуки, К .; Tonien, D .; и другие. (2006). «Парадокс дня рождения для множественных столкновений». В Rhee M.S., Lee B. (ed.). Конспект лекций по информатике, том 4296. Берлин: Springer. Дои:10.1007/11927587_5. Информационная безопасность и криптология - ICISC 2006.
14. З. Э. Шнабель (1938) Оценка общей численности рыб в озере., Американский математический ежемесячный журнал 45, 348–352.
15. М. К. Вендл (2003) Вероятность столкновения между множествами случайных величин, Статистика и вероятностные письма 64(3), 249–254.
16. М. Абрамсон и У. О. Дж. Мозер (1970) Еще сюрпризы на день рождения, Американский математический ежемесячный журнал 77, 856–858
17. Могу, Мэтт. "Столкновение хеш-коллизий с парадоксом дня рождения". Блог Мэтта Мая. Получено 17 июля 2015.
18. Кнут, Д. Э. (1973). Искусство программирования. Vol. 3, Сортировка и поиск. Ридинг, Массачусетс: Эддисон-Уэсли. ISBN  978-0-201-03803-3.
19. Flajolet, P .; Grabner, P.J .; Kirschenhofer, P .; Продингер, Х. (1995). «О Q-функции Рамануджана». Журнал вычислительной и прикладной математики. 58: 103–116. Дои:10.1016 / 0377-0427 (93) E0258-N.
20. Кормен; и другие. Введение в алгоритмы.
21. Флетчер, Джеймс (16 июня 2014 г.). «Парадокс дня рождения на чемпионате мира». bbc.com. BBC. Получено 27 августа 2015.
22. Voracek, M .; Tran, U. S .; Форманн, А. К. (2008). "День рождения и проблемы с партнером по рождению: неправильные представления о вероятности среди студентов-психологов, посетителей и персонала казино". Перцептивные и моторные навыки. 106 (1): 91–103. Дои:10,2466 / пмс.106.1.91-103. PMID  18459359. S2CID  22046399.
23. Borgs, C .; Chayes, J .; Питтель, Б. (2001). «Фазовый переход и масштабирование конечного размера в задаче целочисленного разбиения». Случайные структуры и алгоритмы. 19 (3–4): 247–288. Дои:10.1002 / RS.10004. S2CID  6819493.

Список используемой литературы

• Abramson, M .; Мозер, В. О. Дж. (1970). «Еще сюрпризы на день рождения». Американский математический ежемесячный журнал. 77 (8): 856–858. Дои:10.2307/2317022. JSTOR  2317022.
• Блум, Д. (1973). «Проблема дня рождения». Американский математический ежемесячный журнал. 80 (10): 1141–1142. Дои:10.2307/2318556. JSTOR  2318556.
• Кемени, Джон Дж .; Снелл, Дж. Лори; Томпсон, Джеральд (1957). Введение в конечную математику (Первое изд.).
• Кламкин, М .; Ньюман, Д. (1967). «Продление сюрприза на день рождения». Журнал комбинаторной теории. 3 (3): 279–282. Дои:10.1016 / с0021-9800 (67) 80075-9.
• Маккинни, Э. Х. (1966). «Обобщенная проблема дня рождения». Американский математический ежемесячный журнал. 73 (4): 385–387. Дои:10.2307/2315408. JSTOR  2315408.
• Шнепс, Лейла; Колмез, Корали (2013). «Математическая ошибка номер 5. Случай Дайаны Сильвестр: анализ холодного попадания». Математика на пробу. Как числа используются и злоупотребляют в зале суда. Основные книги. ISBN  978-0-465-03292-1.
• Сай М. Блиндер (2013). Руководство по основам математики: обзор для студентов-физиков, химиков и инженеров. Эльзевир. С. 5–6. ISBN  978-0-12-407163-6.

внешние ссылки

• Парадокс дня рождения с учетом дней рождения в високосном году
• Вайсштейн, Эрик В. "Проблема дня рождения". MathWorld.
• Юмористическая статья, объясняющая парадокс
• Эксперимент по случаю дня рождения SOCR EduMaterials
• Понимание проблемы дня рождения (объяснение лучше)
• Евророждение 2012. Проблема дня рождения. Практический футбольный пример парадокса дня рождения.
• Грайм, Джеймс. «23: Вероятность дня рождения». Numberphile. Брэди Харан. Архивировано из оригинал на 2017-02-25. Получено 2013-04-02.
• Вычисление вероятностей проблемы рождения в WolframAlpha