Семейство гексагональных кристаллов - Hexagonal crystal family - Wikipedia
| Кристаллическая система | Тригональный | Шестиугольный | |
|---|---|---|---|
| Решетчатая система |  Ромбоэдрический |  Шестиугольный | |
| Пример |  Доломит |  Киноварь |  Берил |
В кристаллография, то гексагональное кристаллическое семейство один из шести хрустальные семьи, который включает две кристаллические системы (гексагональную и тригональный) и две системы решеток (гексагональная и ромбоэдрический).
Семейство гексагональных кристаллов состоит из 12 точечных групп, так что по крайней мере одна из их пространственных групп имеет гексагональную решетку в качестве основной решетки и представляет собой объединение гексагональной кристаллической системы и тригональной кристаллической системы.[1] С ним связаны 52 космические группы, и это именно те, чьи Решетка Браве гексагональный или ромбоэдрический.
Решетчатые системы
Семейство гексагональных кристаллов состоит из двух решетчатые системы: шестиугольная и ромбоэдрическая /тригональный.[2] Каждая решетчатая система состоит из одной решетки Браве.

| Решетка Браве | Шестиугольный | Ромбоэдрический |
|---|---|---|
| Символ Пирсона | л.с. | час |
| Шестиугольный ячейка |  | 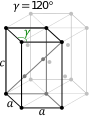 |
| Ромбоэдрический ячейка |  | 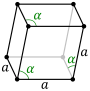 |
В гексагональном семействе кристалл условно описывается правой ромбический призма элементарная ячейка с двумя равными осями (а к а), включенный угол 120 ° (γ) и высотой (c, который может отличаться от а) перпендикулярно двум осям основания.
Гексагональная элементарная ячейка для ромбоэдрической решетки Браве - это R-центрированная ячейка, состоящая из двух дополнительных узлов решетки, которые занимают одну диагональ тела элементарной ячейки. Это можно сделать двумя способами, которые можно рассматривать как две нотации, представляющие одну и ту же структуру. В обычном так называемом реверсе дополнительные точки решетки находятся в координатах (2⁄3, 1⁄3, 1⁄3) и (1⁄3, 2⁄3, 2⁄3), тогда как в альтернативной обратной установке они находятся в координатах (1⁄3,2⁄3,1⁄3) и (2⁄3,1⁄3,2⁄3).[3] В любом случае всего на элементарную ячейку приходится 3 точки решетки, и решетка не является примитивной.
Решетки Браве в семействе гексагональных кристаллов также можно описать ромбоэдрическими осями.[4][5] Элементарная ячейка представляет собой ромбоэдр (отсюда и название ромбоэдрической решетки). Это элементарная ячейка с параметрами а = б = c; α = β = γ ≠ 90°.[6] На практике чаще используется гексагональное описание, потому что легче иметь дело с системой координат с двумя углами 90 °. Однако ромбоэдрические оси часто указываются (для ромбоэдрической решетки) в учебниках, потому что эта ячейка показывает 3м симметрия кристаллической решетки.
Ромбоэдрическая элементарная ячейка для гексагональной решетки Браве является D-центрированной[7] ячейка, состоящая из двух дополнительных узлов решетки, занимающих одну диагональ тела элементарной ячейки с координатами (1⁄3, 1⁄3, 1⁄3) и (2⁄3, 2⁄3, 2⁄3). Однако такое описание используется редко.
Кристаллические системы
| Кристаллическая система | Требуемые симметрии точечной группы | Группы точек | Космические группы | Решетчатая система |
|---|---|---|---|---|
| Тригональный | 1 тройная ось вращения | 5 | 7 | Ромбоэдрический |
| 18 | Шестиугольный | |||
| Шестиугольный | 1 шестикратная ось вращения | 7 | 27 |
Семейство гексагональных кристаллов состоит из двух кристаллические системы: треугольная и шестиугольная. Кристаллическая система - это набор точечные группы в котором сами точечные группы и соответствующие им космические группы закреплены за решетчатая система (см. таблицу в Система кристаллов # Классы кристаллов ).
Тригональная кристаллическая система состоит из 5 точечных групп, которые имеют одну тройную ось вращения, которая включает пространственные группы с 143 по 167. Эти 5 точечных групп имеют 7 соответствующих пространственных групп (обозначенных R), присвоенных системе ромбоэдрической решетки, и 18 соответствующие пространственные группы (обозначаемые P), относящиеся к системе гексагональной решетки.
Гексагональная кристаллическая система состоит из 7 точечных групп, которые имеют одну шестикратную ось вращения. Эти 7 точечных групп имеют 27 пространственных групп (от 168 до 194), все из которых относятся к системе гексагональной решетки. Графитовый является примером кристалл который кристаллизуется в гексагональной кристаллической системе.
Кристалл классы
Тригональная кристаллическая система
Тригональная кристаллическая система - единственная кристаллическая система, точечные группы которой имеют более одного решетчатая система связаны со своими пространственными группами: появляются гексагональная и ромбоэдрическая решетки.
5 точечных групп в этой кристаллической системе перечислены ниже с их международным номером и обозначениями, их пространственными группами в названии и примерами кристаллов.[8][9][10]
| Космическая группа № | Группа точек | Тип | Примеры | Космические группы | |||||
|---|---|---|---|---|---|---|---|---|---|
| Имя[11] | Intl | Schoen. | Сфера. | Кокс. | Шестиугольный | Ромбоэдрический | |||
| 143–146 | Тригонально-пирамидальный | 3 | C3 | 33 | [3]+ | энантиоморфный полярный | карлинит, ярозит | P3, P31, P32 | R3 |
| 147–148 | Ромбоэдрический | 3 | C3i (S6) | 3× | [2+,6+] | центросимметричный | доломит, ильменит | п3 | р3 |
| 149–155 | Трехгранный трапециевидный | 32 | D3 | 223 | [2,3]+ | энантиоморфный | абхурит, альфа-кварц (152, 154), киноварь | P312, P321, P3112, P3121, P3212, P3221 | R32 |
| 156–161 | Дитригонал пирамидальный | 3м | C3в | *33 | [3] | полярный | шерл, церит, турмалин, алунит, танталат лития | P3m1, P31m, P3c1, P31c | R3m, R3c |
| 162–167 | Дитригональный скаленоэдр | 3м | D3D | 2*3 | [2+,6] | центросимметричный | сурьма, гематит, корунд, кальцит, висмут | п31м, П31c, P3m1, P3c1 | р3Мистер3c |
Гексагональная кристаллическая система
В точечные группы (кристаллические классы) в этой кристаллической системе перечислены ниже, за ними следуют их представления в Герман-Моген или международное обозначение и Обозначение Шенфлиса, и минеральная примеры, если они есть.[1][12]
| Космическая группа № | Группа точек | Тип | Примеры | Космические группы | ||||
|---|---|---|---|---|---|---|---|---|
| Имя[11] | Intl | Schoen. | Сфера. | Кокс. | ||||
| 168–173 | Шестиугольная пирамидальная | 6 | C6 | 66 | [6]+ | энантиоморфный полярный | нефелин, канкринит | P6, P61, P65, P62, P64, P63 |
| 174 | Тригональный дипирамидальный | 6 | C3ч | 3* | [2,3+] | лаурелит и борная кислота | п6 | |
| 175–176 | Гексагональный дипирамидальный | 6 / м | C6ч | 6* | [2,6+] | центросимметричный | апатит, ванадинит | P6 / м, P63/ м |
| 177–182 | Шестиугольный трапеции | 622 | D6 | 226 | [2,6]+ | энантиоморфный | кальсилит и высокий кварц | P622, P6122, стр. 6522, стр. 6222, стр. 6422, стр. 6322 |
| 183–186 | Дигексагональная пирамидальная | 6мм | C6v | *66 | [6] | полярный | зеленокит, вюрцит[13] | P6 мм, P6cc, P63см, P63MC |
| 187–190 | Дитригональный дипирамидальный | 6m2 | D3ч | *223 | [2,3] | бенитоит | п6м2, П6c2, P62м, П62c | |
| 191–194 | Дигексагональный дипирамидальный | 6 / ммм | D6ч | *226 | [2,6] | центросимметричный | берилл | P6 / ммм, P6 / mcc, P63/ мкм, P63/ mmc |
Гексагональный плотно упакованный

Гексагональная плотная упаковка (ГПУ) - это один из двух простых типов атомной упаковки с наивысшей плотностью, другой - гранецентрированная кубическая (ГЦК). Однако, в отличие от ГЦК, это не решетка Браве, так как существует два неэквивалентных набора точек решетки. Вместо этого он может быть построен из гексагональной решетки Браве с использованием двухатомного мотива (дополнительный атом примерно на (2⁄3,1⁄3,1⁄2)), связанный с каждой точкой решетки.[14]
Угол ромбоэдрической решетки
Углы решетки и длины векторов решетки одинаковы как для кубической, так и для ромбоэдрической систем решетки. Углы решетки для простой кубической, гранецентрированной кубической и объемноцентрированной кубической решеток равны π/ 2 радиана, π/ 3 радиана и arccos (-1/3) радианы соответственно.[15] Ромбоэдрическая решетка будет результатом других углов решетки.
Смотрите также
Рекомендации
- ^ а б Дана, Джеймс Дуайт; Hurlbut, Корнелиус Сирл (1959). Руководство Даны по минералогии (17-е изд.). Нью-Йорк: Чепмен-холл. С. 78–89.
- ^ https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Book%3A_Physical_Methods_in_Chemistry_and_Nano_Science_(Barron)/07%3A_Molecular_and_Solid_State_Structure/7.01%3A_Crystal_Structure
- ^ Эдвард Принс (2004). Математические методы в кристаллографии и материаловедении. Springer Science & Business Media. п. 41.
- ^ «Страница не найдена - QuantumWise». Quantumwise.com. Cite использует общий заголовок (помощь)
- ^ "Диаграммы и таблицы космических групп среднего разрешения". img.chem.ucl.ac.uk.
- ^ Эшкрофт, Нил У .; Мермин, Н. Дэвид (1976). Физика твердого тела (1-е изд.). п.119. ISBN 0-03-083993-9.
- ^ Хан (2002), п. 73
- ^ Pough, Frederick H .; Петерсон, Роджер Тори (1998). Полевой справочник по камням и минералам. Houghton Mifflin Harcourt. п. 62. ISBN 0-395-91096-X.
- ^ Hurlbut, Cornelius S .; Кляйн, Корнелис (1985). Руководство по минералогии (20-е изд.). стр.78–89. ISBN 0-471-80580-7.
- ^ «Кристаллография и минералы в кристаллической форме». Webmineral.
- ^ а б Хан (2002), п. 794
- ^ «Кристаллография». Webmineral.com. Получено 2014-08-03.
- ^ «Минералы в гексагональной кристаллической системе, класс дигексагональной пирамиды (6 мм)». Mindat.org. Получено 2014-08-03.
- ^ Джасвон, Морис Аарон (1965-01-01). Введение в математическую кристаллографию. Американский паб Elsevier. Co.
- ^ Хан (2002), п. 747
дальнейшее чтение
- Хан, Тео, изд. (2002). Международные таблицы для кристаллографии, том A: Симметрия пространственных групп. Международные таблицы для кристаллографии. А (5-е изд.). Берлин, Нью-Йорк: Springer-Verlag. Дои:10.1107/97809553602060000100. ISBN 978-0-7923-6590-7.
внешняя ссылка
 СМИ, связанные с Шестиугольные решетки в Wikimedia Commons
СМИ, связанные с Шестиугольные решетки в Wikimedia Commons- Минералогическая база данных
