Плотная упаковка равных сфер - Close-packing of equal spheres - Wikipedia

Иллюстрация плотной упаковки одинаковых сфер как в ГПУ (слева), так и в ГЦК (справа) решетках

В геометрия, плотная упаковка равных сферы представляет собой плотное расположение конгруэнтных сфер в бесконечном регулярном расположении (или решетка ). Карл Фридрих Гаусс доказал, что самая высокая средняя плотность - то есть наибольшая часть пространства, занятая сферами, - может быть достигнута решетка упаковка

${\displaystyle {\frac {\pi }{3{\sqrt {2}}}}\simeq 0.74048.}$

Такой же плотность упаковки также может быть достигнуто путем альтернативного наложения одних и тех же плотноупакованных плоскостей сфер, включая структуры, апериодические в направлении наложения. В Гипотеза Кеплера заявляет, что это самая высокая плотность, которая может быть достигнута при любом расположении сфер, регулярном или неправильном. Это предположение было доказано Т. К. Хейлз.^[1][2] Наибольшая плотность известна только в случае 1, 2, 3, 8 и 24 измерений.^[3]

Много кристалл структуры основаны на плотной упаковке атомов одного типа или на плотной упаковке больших ионов с меньшими ионами, заполняющими промежутки между ними. Кубическая и гексагональная конфигурации очень близки друг к другу по энергии, и может быть трудно предсказать, какая форма будет предпочтительнее, исходя из первых принципов.

Решетки FCC и HCP

Расположение ГЦК в 4-х осевом направлении

fcc		hcp
В fcc расположение может быть ориентировано в двух разных плоскостях, квадратной или треугольной. Их можно увидеть в кубооктаэдр с 12 вершинами, представляющими положения 12 соседних сфер вокруг одной центральной сферы. В hcp расположение можно увидеть в треугольной ориентации, но чередуются два положения сфер в треугольная ортобикупола расположение.

Есть две простые регулярные решетки, которые достигают этой наивысшей средней плотности. Они называются гранецентрированная кубическая (fcc) (также называемый кубический плотно упакованный) и шестиугольник плотно упакованный (hcp), исходя из их симметрия. Оба основаны на листах сфер, расположенных в вершинах треугольной плитки; они различаются тем, как листы уложены друг на друга. ГЦК-решетка также известна математикам как решетка, порожденная A₃ корневая система.^[4]

Проблема с пушечным ядром

Основная статья: Проблема с пушечным ядром

Ядра сложены на треугольник (передний) и прямоугольные (назад) база, оба fcc решетки.

Проблема плотной упаковки сфер впервые математически проанализирована Томас Харриот около 1587 года, после того, как сэр Уолтер Рэли в их экспедиции в Америку.^[5] Пушечные ядра обычно складывались в прямоугольную или треугольную деревянную раму, образуя трех- или четырехстороннюю пирамиду. Обе конструкции создают гранецентрированную кубическую решетку - с разной ориентацией по отношению к земле. Гексагональная плотная упаковка приведет к шестигранной пирамиде с шестиугольным основанием.

Снежки сложены в стопку для подготовки к битва снежками. Передняя пирамида шестиугольная плотно упакованная, а задняя гранецентрированная кубическая.

В проблема с пушечным ядром спрашивает, какие плоские квадратные конструкции пушечных ядер можно сложить в квадратную пирамиду. Эдуард Лукас сформулировал проблему как Диофантово уравнение ${\displaystyle \sum _{n=1}^{N}n^{2}=M^{2}}$ или же ${\displaystyle {\frac {1}{6}}N(N+1)(2N+1)=M^{2}}$ и предположил, что единственными решениями являются ${\displaystyle N=1,M=1,}$ и ${\displaystyle N=24,M=70}$. Здесь ${\displaystyle N}$ - количество слоев в пирамидальной компоновке и ${\displaystyle M}$ - количество ядер по краю плоской квадратной конструкции.

Расположение и интервал

И в схемах ГЦК, и в ГПУ каждая сфера имеет двенадцать соседей. Для каждой сферы есть один зазор, окруженный шестью сферами (восьмигранный ) и два меньших промежутка, окруженные четырьмя сферами (тетраэдрические). Расстояния до центров этих промежутков от центров окружающих сфер равны √​³⁄₂ для тетраэдра и √2 для октаэдра, когда радиус сферы равен 1.

По сравнению с опорным слоем с позиционированием, еще два позиционирование В и С, возможны. Любая последовательность A, B и C без непосредственного повторения одной и той же возможна и дает одинаково плотную упаковку для сфер заданного радиуса.

Самыми регулярными являются

• fcc = ABC ABC ABC ... (каждый третий слой одинаковый)
• hcp = AB AB AB AB ... (все остальные слои такие же).

Существует бесчисленное множество неупорядоченных расположений плоскостей (например, ABCACBABABAC ...), которые иногда собирательно называют «упаковками Барлоу» в честь кристаллографа. Уильям Барлоу^[6]

В плотной упаковке расстояние между центрами сфер в ху Плоскость представляет собой простую мозаику в виде сот с шагом (расстоянием между центрами сфер) в один диаметр сферы. Расстояние между центрами сфер, проецируемое на z (вертикальная) ось:

${\displaystyle {\text{pitch}}_{Z}={\sqrt {6}}\cdot {d \over 3}\approx 0.816\,496\,58d,}$

куда d диаметр шара; это следует из тетраэдрического расположения плотноупакованных сфер.

В координационный номер ГПУ и ГЦК составляет 12, а их коэффициенты упаковки атомов (НПФ) равны указанному выше числу 0,74.

Сравнение hcp и fcc
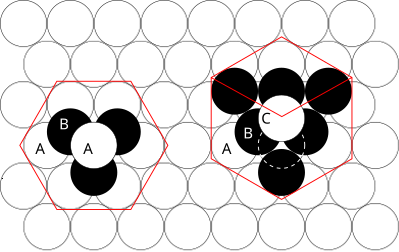Рисунок 1 - Решетка ГПУ (слева) и решетка ГЦК (справа). Схема каждого соответствующего Решетка Браве отображается красным. Буквы указывают, какие слои совпадают. В ГПУ-матрице есть два слоя «А», где все сферы находятся в одинаковом положении. Все три слоя в стеке ГЦК разные. Обратите внимание, что наложение ГЦК можно преобразовать в наложение ГПУ путем перемещения самой верхней сферы, как показано пунктирным контуром.

фигура 2 - Здесь показана стопка из одиннадцати сфер hcp решетка, показанная на Рисунок 1. Стек ГПУ отличается от трех верхних уровней стека ГЦК, показанных на Рисунок 3 только на самом низком уровне; его можно преобразовать в fcc соответствующим поворотом или перемещением.	Рисунок 3 – Томас Харриот, около 1585 г., впервые задумался о математике расположение пушечного ядра или же стек пушечных ядер, который имеет fcc решетка. Обратите внимание, как соседние шары по каждому краю регулярного тетраэдр все окружающие стек находятся в прямом контакте друг с другом. Этого не происходит в решетке ГПУ, как показано на фигура 2.

Генерация решетки

При формировании любой решетки упаковки сфер в первую очередь следует обратить внимание на то, что всякий раз, когда две сферы соприкасаются, прямая линия может быть проведена от центра одной сферы к центру другой, пересекая точку контакта. Расстояние между центрами по кратчайшему пути, а именно эта прямая линия, поэтому будет р₁ + р₂ куда р₁ - радиус первой сферы и р₂ - радиус второго. В плотной упаковке все сферы имеют общий радиус, р. Следовательно, два центра просто будут иметь расстояние 2р.

Простая ГПУ решетка

Анимация создания решетки плотной упаковки. Примечание. Если третий слой (не показан) находится непосредственно над первым слоем, то строится решетка HCP. Если третий слой накладывается на отверстия в первом слое, создается решетка FCC.

Чтобы сформировать гексагональную плотную упаковку сфер A-B-A-B -..., координатные точки решетки будут центрами сфер. Предположим, цель - заполнить коробку сферами согласно hcp. Коробка будет помещена на Икс-у-z координатное пространство.

Сначала сформируйте ряд сфер. Все центры будут лежать на прямой линии. Их Икс-координата будет отличаться на 2р поскольку расстояние между центрами соприкасающихся сфер равно 2р. В у-координата и z-координата будут одинаковыми. Для простоты скажем, что шары - это первый ряд, а их у- и z-координаты просто р, так что их поверхности лежат в нулевых плоскостях. Координаты центров первого ряда будут иметь вид (2р, р, р), (4р, р, р), (6р ,р, р), (8р ,р, р), ... .

Теперь сформируйте следующий ряд сфер. Опять же, все центры будут лежать на прямой линии с Икс-координатные разности 2р, но будет смещение расстояния р в Икс-направление так, чтобы центр каждой сферы в этом ряду совпадал с Икс-координата соприкосновения двух сфер в первом ряду. Это позволяет сферам нового ряда перемещаться ближе к первому ряду, пока все сферы нового ряда не коснутся двух сфер первого ряда. Поскольку новые сферы трогать две сферы, их центры образуют равносторонний треугольник с центрами этих двух соседей. Длины сторон все 2р, поэтому высота или у-координатная разница между рядами составляет √3р. Таким образом, эта строка будет иметь такие координаты:

${\displaystyle \left(r,r+{\sqrt {3}}r,r\right),\ \left(3r,r+{\sqrt {3}}r,r\right),\ \left(5r,r+{\sqrt {3}}r,r\right),\ \left(7r,r+{\sqrt {3}}r,r\right),\dots .}$

Первая сфера этого ряда касается только одной сферы в исходном ряду, но ее положение совпадает с положением остальной части ряда.

Следующая строка следует этой схеме смещения Икс-координировать р и у-координировать √3. Добавляйте строки, пока не дойдете до Икс и у максимальные границы коробки.

В схеме укладки A-B-A-B -... нечетные пронумерованные самолеты сфер будут иметь точно такие же координаты, за исключением разницы в шаге z-координаты и четные номера самолеты сфер будут иметь одинаковые Икс- и у-координаты. Оба типа плоскостей формируются по схеме, упомянутой выше, но исходное место для первый первая сфера строки будет другой.

Используя плоскость, описанную выше как плоскость № 1, плоскость A, поместите сферу поверх этой плоскости так, чтобы она касалась трех сфер в плоскости A. Все три сферы уже касаются друг друга, образуя равносторонний треугольник, и, поскольку все они касаются новой сферы, четыре центра образуют правильный тетраэдр.^[7] Все стороны равны 2р потому что все стороны образованы двумя соприкасающимися сферами. Высота которого или z- разница координат между двумя «плоскостями» составляет √6р2/3. Это в сочетании со смещениями в Икс и у-координаты задают центры первого ряда в плоскости B:

${\displaystyle \left(r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(3r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(5r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(7r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\dots .}$

Координаты второй строки соответствуют шаблону, описанному выше, и составляют:

${\displaystyle \left(2r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(4r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(6r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(8r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\dots .}$

Разница со следующим самолетом, самолетом А, снова √6р2/3 в z-направление и сдвиг в Икс и у чтобы соответствовать тем Икс- и у-координаты первой плоскости А.^[8]

В общем случае координаты центров сфер можно записать как:

${\displaystyle {\begin{bmatrix}2i+((j\ +\ k){\bmod {2}})\\{\sqrt {3}}\left[j+{\frac {1}{3}}(k{\bmod {2}})\right]\\{\frac {2{\sqrt {6}}}{3}}k\end{bmatrix}}r}$

куда я, j и k индексы, начинающиеся с 0 для Икс-, у- и z-координаты.

Индексы Миллера

Основная статья: Индекс Миллера

Индекс Миллера – Браве для ГПУ-решетки

Кристаллографические особенности ГПУ-систем, такие как векторы и семейства атомных плоскостей, могут быть описаны с помощью четырехзначного Индекс Миллера обозначение ( hkil ) в котором третий индекс я обозначает удобный, но вырожденный компонент, который равен -час − k. В час, я и k направления указателей разделены на 120 ° и, следовательно, не ортогональны; то л компонент взаимно перпендикулярен час, я и k указатель направлений.

Заполнение оставшегося места

ГЦК- и ГПУ-упаковки - это самые плотные известные упаковки из равных сфер с наивысшей симметрией (наименьшие повторяющиеся единицы). сферические упаковки известны, но они включают неравномерная упаковка сфер.Плотность упаковки 1, полностью заполняющая пространство, требует несферических форм, таких как соты.

Замена каждой точки контакта между двумя сферами ребром, соединяющим центры соприкасающихся сфер, дает тетраэдры и октаэдры с равной длиной ребер. четырехгранно-октаэдрические соты.Установка ГПУ производит спиральные четырехгранно-октаэдрические соты Если вместо этого каждая сфера дополнена точками в пространстве, которые находятся ближе к ней, чем к любой другой сфере, образуются двойники этих сот: ромбические додекаэдрические соты для fcc, а трапеции-ромбические додекаэдрические соты для hcp.

Сферические пузырьки появляются в мыльной воде в виде ГЦК или ГПУ, когда вода в промежутках между пузырьками стекает. Этот паттерн также приближается к ромбические додекаэдрические соты или же трапеции-ромбические додекаэдрические соты. Однако такие пены с ГЦК или ГПУ с очень малым содержанием жидкости нестабильны, так как они не удовлетворяют требованиям Законы Плато. В Пена Кельвина и Пена Weaire – Phelan более стабильны, имея меньшую межфазную энергию в пределе очень малого содержания жидкости.^[9]

Смотрите также

• Кубическая кристаллическая система
• Постоянная Эрмита
• Случайная близкая упаковка
• Упаковка сфер
• Набивка цилиндрической сферы

Примечания

1. Хейлз, Т. (1998). «Обзор гипотезы Кеплера». arXiv:математика / 9811071v2.
2. Шпиро, Джордж (2003). «Математика: складывается ли доказательство?». Природа. 424 (6944): 12–13. Bibcode:2003Натура.424 ... 12С. Дои:10.1038 / 424012a.
3. Cohn, H .; Кумар, А .; Miller, S.D .; Радченко, Д .; Вязовская, М. (2017). «Проблема упаковки сфер в размерности 24». Анналы математики. 185 (3): 1017–1033. arXiv:1603.06518. Дои:10.4007 / анналы.2017.185.3.8.
4. Конвей, Джон Хортон; Слоан, Нил Джеймс Александр; Баннаи, Эйити (1999). Сферические упаковки, решетки и группы. Springer. Раздел 6.3.
5. Дорогой, Дэвид. "Проблема с пушечным ядром". Интернет-энциклопедия науки.
6. Барлоу, Уильям (1883). «Вероятная природа внутренней симметрии кристаллов» (PDF). Природа. 29 (738): 186–188. Bibcode:1883Натура..29..186Б. Дои:10.1038 / 029186a0.
7. "на упаковке сферы". Grunch.net. Получено 2014-06-12.
8. Вайсштейн, Эрик В. "Гексагональная плотная упаковка". MathWorld.
9. Кантат, Изабель; Коэн-Аддад, Сильви; Элиас, Флоренция; Гранер, Франсуа; Хёлер, Рейнхард; Flatman, Рут; Питуа, Оливье (2013). Пены, структура и динамика. Оксфорд: Издательство Оксфордского университета. ISBN  9780199662890.

внешняя ссылка

• П. Кришна и Д. Панди, Международный союз кристаллографии "Плотноупакованные структуры", Университетский колледж Кардифф Пресс. Кардифф, Уэльс. PDF