Ромбические додекаэдрические соты - Rhombic dodecahedral honeycomb
| Ромбические додекаэдрические соты | |
|---|---|
 | |
| Тип | выпуклые однородные соты двойной |
| Диаграмма Кокстера-Дынкина | |
| Тип ячейки |  Ромбический додекаэдр V3.4.3.4 |
| Типы лица | Ромб |
| Космическая группа | FM3м (225) |
| Обозначение Кокстера | ½, [1+,4,3,4] , [4,31,1] ×2, <[3[4]]> |
| Двойной | четырехгранно-октаэдрические соты |
| Характеристики | реберно-транзитивный, лицо переходный, клеточно-транзитивный |
В ромбические додекаэдрические соты (также додекаэдрил) является заполняющим мозаика (или же соты ) в трехмерном евклидовом пространстве. Это Диаграмма Вороного из гранецентрированная кубическая сфера-упаковка, которая имеет максимально плотную упаковку одинаковых сфер в обычном пространстве (см. Гипотеза Кеплера ).
Геометрия
Он состоит из копий одного клетка, то ромбический додекаэдр. Все лица ромбовидные, с диагоналями в соотношении 1:√2. По три ячейки встречаются на каждом краю. Таким образом, соты клеточно-транзитивный, лицо переходный, и реберно-транзитивный; но это не так вершинно-транзитивный, так как имеет два типа вершин. Вершины с тупыми углами ромбической грани имеют 4 ячейки. В вершинах с острыми углами ромбической грани по 6 ячеек.
Ромбический додекаэдр может быть скручен на одном из его шестиугольных поперечных сечений, чтобы образовать трапеции-ромбический додекаэдр, которая является ячейкой похожей мозаики, Диаграмма Вороного шестиугольной плотная упаковка.
 |  Соты можно получить из альтернативной мозаики куба, добавив пирамиду к каждой грани каждого куба. |  Вид изнутри на ромбические додекаэдрические соты. |
Раскраски
Ячейкам можно присвоить 4 цвета в квадратных слоях из 2 цветов, где соседние грани имеют разные цвета, и 6 цветов в шестиугольных слоях из 3 цветов, где ячейки одного цвета не имеют никакого контакта.
| 4 цвета | 6 цветов |
|---|---|
 | 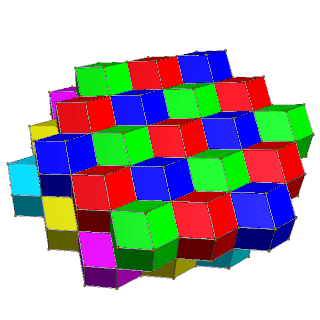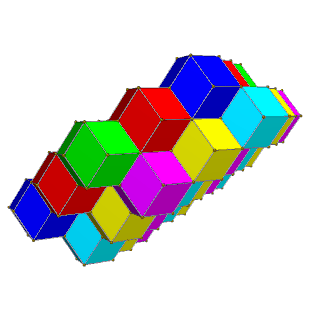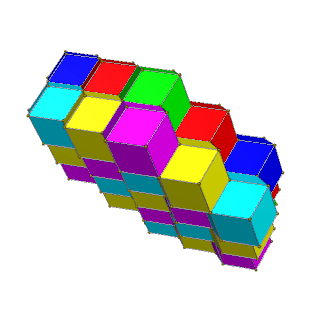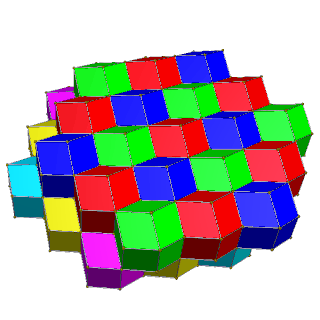 |
| Чередуйте квадратные слои желтого, синего с красным и зеленым | Чередуйте шестиугольные слои красного, зеленого, синего и пурпурного, желтого, голубого цветов. |
Связанные соты
В ромбические додекаэдрические соты можно разрезать на треугольные трапециевидные соты с каждым ромбическим додекаэдром, разрезанным на 4 тригональные трапецииэдры. Каждый ромбический додекаэдр можно также разрезать с центром на 12 ромбических пирамид ромбические пирамидальные соты.
Додекаэдрические соты трапециевидной формы
| Додекаэдрические соты трапециевидной формы | |
|---|---|
 | |
| Тип | выпуклые однородные соты двойной |
| Тип ячейки | трапеции-ромбический додекаэдр VG3.4.3.4 |
| Типы лица | ромб, трапеция |
| Группа симметрии | P63/ mmc |
| Двойной | спиральные четырехгранно-октаэдрические соты |
| Характеристики | однородный по краям, однородный по лицу, однородный по ячейкам |
В трапеции-ромбические додекаэдрические соты заполняет пространство мозаика (или же соты ) в трехмерном евклидовом пространстве. Он состоит из копий одной ячейки, трапеции-ромбический додекаэдр. Это похоже на более симметричные ромбические додекаэдрические соты, у которых все 12 граней являются ромбами.
Связанные соты
Это двойник вершинно-транзитивный спиральные четырехгранно-октаэдрические соты.
Ромбические пирамидальные соты
| Ромбические пирамидальные соты | |
|---|---|
| (Нет изображения) | |
| Тип | Двойные однородные соты |
| Диаграммы Кокстера-Дынкина | |
| Клетка | ромбический пирамида |
| Лица | Ромб Треугольник |
| Группы Кокстера | [4,31,1], [3[4]], |
| Группа симметрии | FM3м (225) |
| фигуры вершин | |
| Двойной | Кантик кубические соты |
| Характеристики | Клеточно-транзитивный |
В ромбические пирамидальные соты или же полусплющенный октаэдр равномерное заполнение пространства мозаика (или же соты ) в трехмерном евклидовом пространстве.
Эти соты можно рассматривать как ромбические додекаэдрические соты, с ромбические додекаэдры рассеченный с центром в 12 ромбических пирамид.
 ромбические додекаэдрические соты | 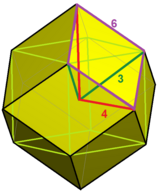 Ромбоэдрическое рассечение |  Внутри куба |
Связанные соты
Он двойственен кантик кубические соты:
Смотрите также
Рекомендации
- Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. стр. 168. ISBN 0-486-23729-X.






