Тетраэдрально-восьмигранные соты - Tetrahedral-octahedral honeycomb

Чередующиеся кубические соты
Тип	Равномерные соты
Семья	Чередующиеся гиперкубические соты Простые соты
Индексирование[1]	J21,31,51, А2 W9, ГРАММ1
Символы Шлефли	ч {4,3,4} {3^[4]} ht0,3{4,3,4} ч {4,4} ч {∞} ht0,2{4,4} ч {∞} h {∞} h {∞} h {∞} s {∞} s {∞} s {∞}
Диаграммы Кокстера	= = = =
Клетки	{3,3} {3,4}
Лица	треугольник {3}
Край фигура	[{3,3}.{3,4}]^2 (прямоугольник )
Фигура вершины	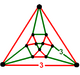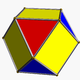(кубооктаэдр )
Группа симметрии	FM3м (225)
Группа Кокстера	${\displaystyle {\tilde {B}}_{3}}$, [4,3^1,1]
Двойной	Додекаэдрил ромбические додекаэдрические соты Клетка:
Характеристики	вершинно-транзитивный, реберно-транзитивный, квазирегулярные соты

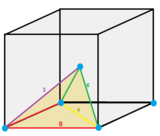
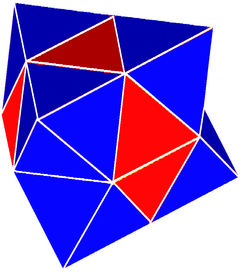
В четырехгранно-октаэдрические соты, чередующиеся кубические соты является квазирегулярным заполнением пространства мозаика (или же соты ) в Евклидово 3-пространство. Он состоит из чередующихся регулярных октаэдры и тетраэдры в соотношении 1: 2.

Другие имена включают полукубические соты, полукубическая ячейка, или же тетрагональная дисфеноидальная клетка. Джон Хортон Конвей называет эту соту тетроктаэдрил, и его двойственный додекаэдрил.

это вершинно-транзитивный с 8 тетраэдры и 6 октаэдры вокруг каждого вершина. это реберно-транзитивный с двумя тетраэдрами и двумя октаэдрами, чередующимися на каждом ребре.

А геометрические соты это заполнение пространства из многогранник или многомерный клетки, чтобы не было зазоров. Это пример более общего математического черепица или же мозаика в любом количестве измерений.

Соты обычно строятся из обычных Евклидово ("плоское") пространство, как и выпуклые однородные соты. Они также могут быть построены в неевклидовы пространства, Такие как гиперболические однородные соты. Любой конечный равномерный многогранник можно спроецировать на его окружающая сфера образовывать однородные соты в сферическом пространстве.

Это часть бесконечной семьи однородные соты называется чередующиеся гиперкубические соты, сформированный как чередование из гиперкубических сот и состоит из полугиперкуб и кросс-многогранник грани. Он также является частью еще одного бесконечного семейства однородных сот, называемых простые соты.

В этом случае 3-мерного пространства кубические соты чередуется, уменьшая кубические ячейки до тетраэдров, а удаленные вершины создают октаэдрические пустоты. В качестве такового он может быть представлен расширенным Символ Шлефли h {4,3,4} как содержащий половина вершины {4,3,4} кубической соты.

Есть похожие соты под названием спиральные четырехгранно-октаэдрические соты в котором слои повернуты на 60 градусов, поэтому половина ребер имеет соседние, а не чередующиеся тетраэдры и октаэдры.

Симметрия тетраэдрально-октаэдрических сот может быть удвоена путем размещения тетраэдров на октаэдрических ячейках, создавая неравномерные соты, состоящие тетраэдры и октаэдры (как треугольные антипризмы). Его вершина - фигура усеченный триакис тетраэдр порядка 3. Эти соты являются двойным усеченные четырехгранные соты triakis, с усеченный четырехгранный триак клетки.

Декартовы координаты

Для чередующиеся кубические сотыс ребрами, параллельными осям, и длиной ребра, равной 1, Декартовы координаты вершин равны: (Для всех целых значений: я,j,k с я+j+k четное )

(я, j, k)

На этой диаграмме показан в разобранном виде ячеек, окружающих каждую вершину.

Симметрия

Есть две светоотражающие конструкции и многие чередующиеся кубические соты единицы; Примеры:

Симметрия	${\displaystyle {\tilde {B}}_{3}}$, [4,3^1,1] = ½${\displaystyle {\tilde {C}}_{3}}$, [1^+,4,3,4]	${\displaystyle {\tilde {A}}_{3}}$, [3^[4]] = ½${\displaystyle {\tilde {B}}_{3}}$, [1^+,4,3^1,1]	[[(4,3,4,2^+)]]	[(4,3,4,2^+)]
Космическая группа	FM3м (225)	F43 мес. (216)	я43 мес. (217)	п43 мес. (215)
Изображение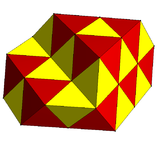
Типы тетраэдров	1	2	3	4
Coxeter диаграмма	=	= =

Чередующиеся кубические сотовые срезы

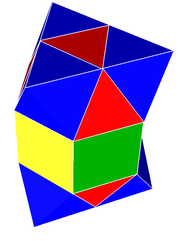
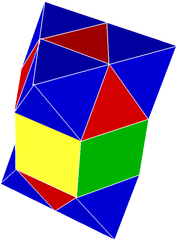
В чередующиеся кубические соты можно разрезать на секции, где новые квадратные грани создаются изнутри октаэдра. Каждый срез будет содержать вверх и вниз квадратные пирамиды и тетраэдры сидя на краях. Второе направление среза не требует новых граней и включает чередование тетраэдра и октаэдра. Эта сотовая плита представляет собой чешуйчатые соты а не однородный, потому что он имеет неоднородные ячейки.

Проекция складыванием

В чередующиеся кубические соты может быть ортогонально проецирован на планарную квадратная черепица по геометрическая складка операция, которая отображает одну пару зеркал друг в друга. Проекция чередующиеся кубические соты создает две офсетные копии квадратной плитки расположение вершин самолета:

Coxeter группа	${\displaystyle {\tilde {A}}_{3}}$	${\displaystyle {\tilde {C}}_{2}}$
Coxeter диаграмма
Изображение
Имя	чередующиеся кубические соты	квадратная черепица

Решетка A3 / D3

Его расположение вершин представляет собой А₃ решетка или же D₃ решетка.^[2][3] Эта решетка известна как гранецентрированная кубическая решетка в кристаллографии и также называется кубическая плотноупакованная решетка поскольку его вершины являются центрами плотной упаковки с равными сферами, которая достигает максимально возможной средней плотности. Тетраэдрически-октаэдрические соты представляют собой трехмерный случай простые соты. Его ячейка Вороного представляет собой ромбический додекаэдр, двойственный кубооктаэдр фигура вершин соты тет-окт.

D⁺
₃ упаковку можно построить объединением двух D₃ (или A₃) решетки. D⁺
_п упаковка только решетка для четных размеров. Число поцелуев 2²=4, (2^п-1 для n <8, 240 для n = 8 и 2n (n-1) для n> 8).^[4]

∪

А^*
₃ или D^*
₃ решетка (также называемая A⁴
₃ или D⁴
₃) можно построить объединением всех четырех A₃ решеток и идентичен расположение вершин из дисфеноидные четырехгранные соты, двойные соты униформы усеченные кубические соты:^[5] Это также объемно центрированный кубический, союз двух кубические соты в двойных позициях.

∪ ∪ ∪ = двойной = ∪ .

В номер поцелуя D^*
₃ решетка 8^[6] и это Мозаика Вороного это усеченные кубические соты, , содержащий все усеченный восьмигранник Клетки Вороного, .^[7]

Связанные соты

C3 соты

[4,3,4], , Группа Кокстера генерирует 15 перестановок однородных сот, 9 с различной геометрией, включая чередующиеся кубические соты. В расширенный кубические соты (также известные как тессерактические соты) геометрически идентичны кубическим сотам.

C3 соты
Космос группа	Фибрифолд	Расширенный симметрия	Расширенный диаграмма	Заказ	Соты
Вечера3м (221)	4^−:2	[4,3,4]		×1	1, 2, 3, 4, 5, 6
FM3м (225)	2^−:2	[1^+,4,3,4] ↔ [4,3^1,1]	↔	Половина	7, 11, 12, 13
я43м (217)	4^о:2	[[(4,3,4,2^+)]]		Половина × 2	(7),
Fd3м (227)	2^+:2	[[1^+,4,3,4,1^+]] ↔ [[3^[4]]]	↔	Квартал × 2	10,
Я3м (229)	8^о:2	[[4,3,4]]		×2	(1), 8, 9

B3 соты

[4,3^1,1], , Группа Кокстера генерирует 9 перестановок однородных сот, 4 с различной геометрией, включая чередующиеся кубические соты.

B3 соты
Космос группа	Фибрифолд	Расширенный симметрия	Расширенный диаграмма	Заказ	Соты
FM3м (225)	2^−:2	[4,3^1,1] ↔ [4,3,4,1^+]	↔	×1	1, 2, 3, 4
FM3м (225)	2^−:2	<[1^+,4,3^1,1]> ↔ <[3^[4]]>	↔	×2	(1), (3)
Вечера3м (221)	4^−:2	<[4,3^1,1]>		×2	5, 6, 7, (6), 9, 10, 11

Соты формата А3

Эти соты - одна из пять отдельных однородных сот^[8] построенный ${\displaystyle {\tilde {A}}_{3}}$ Группа Кокстера. Симметрию можно умножить на симметрию колец в Диаграммы Кокстера – Дынкина:

Соты формата А3
Космос группа	Фибрифолд	Квадрат симметрия	Расширенный симметрия	Расширенный диаграмма	Расширенный группа	Сотовые диаграммы
F43м (216)	1^о:2	а1	[3^[4]]		${\displaystyle {\tilde {A}}_{3}}$	(Никто)
FM3м (225)	2^−:2	d2	<[3^[4]]> ↔ [4,3^1,1]	↔	${\displaystyle {\tilde {A}}_{3}}$×21 ↔ ${\displaystyle {\tilde {B}}_{3}}$	1, 2
Fd3м (227)	2^+:2	g2	[[3^[4]]] или [2^+[3^[4]]]	↔	${\displaystyle {\tilde {A}}_{3}}$×22	3
Вечера3м (221)	4^−:2	d4	<2[3^[4]]> ↔ [4,3,4]	↔	${\displaystyle {\tilde {A}}_{3}}$×41 ↔ ${\displaystyle {\tilde {C}}_{3}}$	4
я3 (204)	8^−o	r8	[4[3^[4]]]^+ ↔ [[4,3^+,4]]	↔	½${\displaystyle {\tilde {A}}_{3}}$×8 ↔ ½${\displaystyle {\tilde {C}}_{3}}$×2	(*)
Я3м (229)	8^о:2		[4[3^[4]]] ↔ [[4,3,4]]		${\displaystyle {\tilde {A}}_{3}}$×8 ↔ ${\displaystyle {\tilde {C}}_{3}}$×2	5

Квазирегулярные соты

Квазирегулярные полихоры и соты: h {4, p, q}
Космос	Конечный	Аффинный	Компактный	Паракомпакт
Schläfli символ	ч {4,3,3}	ч {4,3,4}	ч {4,3,5}	ч {4,3,6}	ч {4,4,3}	ч {4,4,4}
	${\displaystyle \left\{3,{3 \atop 3}\right\}}$	${\displaystyle \left\{3,{4 \atop 3}\right\}}$	${\displaystyle \left\{3,{5 \atop 3}\right\}}$	${\displaystyle \left\{3,{6 \atop 3}\right\}}$	${\displaystyle \left\{4,{4 \atop 3}\right\}}$	${\displaystyle \left\{4,{4 \atop 4}\right\}}$
Coxeter диаграмма	↔	↔	↔	↔	↔	↔
	↔					↔
Изображение
Вершина фигура г {р, 3}

Кантик кубические соты

Кантик кубические соты
Тип	Равномерные соты
Символ Шлефли	час2{4,3,4}
Диаграммы Кокстера	= =
Клетки	т {3,4} г {4,3} т {3,3}
Лица	треугольник {3} квадрат {4} шестиугольник {6}
Фигура вершины	прямоугольный пирамида
Группы Кокстера	[4,3^1,1], ${\displaystyle {\tilde {B}}_{3}}$ [3^[4]], ${\displaystyle {\tilde {A}}_{3}}$
Группа симметрии	FM3м (225)
Двойной	полусплющенный октаэдр Клетка:
Характеристики	вершинно-транзитивный

В кантик кубические соты, кантик кубическая целочисленность или же усеченные полукубические соты равномерное заполнение пространства мозаика (или же соты ) в трехмерном евклидовом пространстве. Он состоит из усеченные октаэдры, кубооктаэдр и усеченные тетраэдры в соотношении 1: 1: 2. Его вершина фигуры прямоугольный пирамида.

Джон Хортон Конвей называет эту соту усеченный тетраоктаэдрил, и его двойственный полусплющенный октаэдр.

 

Симметрия

Он имеет две разные однородные конструкции. В ${\displaystyle {\tilde {A}}_{3}}$ конструкцию можно увидеть с чередованием цветов усеченные тетраэдры.

Симметрия	[4,3^1,1], ${\displaystyle {\tilde {B}}_{3}}$ =<[3^[4]]>	[3^[4]], ${\displaystyle {\tilde {A}}_{3}}$
Космическая группа	FM3м (225)	F43 мес. (216)
Окраска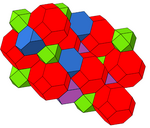
Coxeter	=	=
Фигура вершины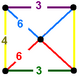

Связанные соты

Это связано с канеллированные кубические соты. Ромбокубооктаэдры уменьшаются до усеченных октаэдров, а кубы уменьшаются до усеченных тетраэдров.

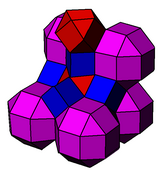скошенный кубический	Кантик кубический
, , рр {4,3}, г {4,3}, {4,3}	, , т {3,4}, г {4,3}, т {3,3}

Рунковские кубические соты

Рунковские кубические соты
Тип	Равномерные соты
Символ Шлефли	час3{4,3,4}
Диаграммы Кокстера	=
Клетки	рр {4,3} {4,3} {3,3}
Лица	треугольник {3} квадрат {4}
Фигура вершины	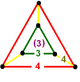усеченный треугольник
Группа Кокстера	${\displaystyle {\tilde {B}}_{4}}$, [4,3^1,1]
Группа симметрии	FM3м (225)
Двойной	четверть кубиля Клетка:
Характеристики	вершинно-транзитивный

В рунические кубические соты или же руническая кубическая целочисленность равномерное заполнение пространства мозаика (или же соты ) в трехмерном евклидовом пространстве. Он состоит из ромбокубооктаэдры, кубики, и тетраэдры в соотношении 1: 1: 2. Его вершина фигуры это усеченный треугольник, с тетраэдром на одном конце, кубом на противоположном конце и тремя ромбокубооктаэдрами вокруг трапециевидных сторон.

Джон Хортон Конвей называет эту соту 3-RCO-триль, и его двойственный четверть кубиля.

Четверть кубиля

Двойник рунические кубические соты называется четверть кубиля, с Диаграмма Кокстера , с лицами в 2 из 4-х авиалайнеров ${\displaystyle {\tilde {B}}_{4}}$, [4,3^1,1] фундаментальная область симметрии.

Ячейки можно рассматривать как 1/4 часть рассеченный куб, используя 4 вершины и центр. Четыре ячейки существуют вокруг 6 ребер и 3 клетки вокруг 3 ребер.

Связанные соты

Это связано с соты кубической формы, с четвертью кубиков чередовались в тетраэдры, а половина расширенный в ромбокубооктаэдры.

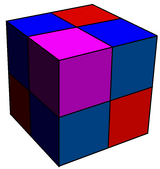Бугристый кубический	Руническая кубическая =
{4,3}, {4,3}, {4,3}, {4,3} , , ,	ч {4,3}, рр {4,3}, {4,3} , ,

Эти соты можно разделить на усеченная квадратная мозаика самолеты, используя восьмиугольники центры ромбокубооктаэдров, создающие квадратные купола. Этот чешуйчатые соты представлен диаграммой Кокстера , а символ s₃{2,4,4}, с обозначение Кокстера симметрия [2⁺,4,4].

.

---

Рунсикантические кубические соты

Рунсикантические кубические соты
Тип	Равномерные соты
Символ Шлефли	час2,3{4,3,4}
Диаграммы Кокстера	=
Клетки	tr {4,3} т {4,3} т {3,3}
Лица	треугольник {3} квадрат {4} шестиугольник {6} восьмиугольник {8}
Фигура вершины	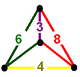зеркальная клиновидная кость
Группа Кокстера	${\displaystyle {\tilde {B}}_{4}}$, [4,3^1,1]
Группа симметрии	FM3м (225)
Двойной	полупирамидилль Клетка:
Характеристики	вершинно-транзитивный

В рунические кубические соты или же руническая кубическая клетчатка равномерное заполнение пространства мозаика (или же соты ) в трехмерном евклидовом пространстве. Он состоит из усеченные кубооктаэдры, усеченные кубики и усеченные тетраэдры в соотношении 1: 1: 2, с зеркальная клиновидная кость вершина фигуры. Это связано с разнесенные кубические соты.

Джон Хортон Конвей называет эту соту f-tCO-trille, и его двойственный полупирамидилль.

Полупирамидилла

Двойной к усеченные кубические соты называется полупирамидилль, с Диаграмма Кокстера . Грани существуют в 3 из 4 гиперплоскостей [4,3^1,1], ${\displaystyle {\tilde {B}}_{3}}$ Группа Кокстера.

Клетки представляют собой неправильные пирамиды, и их можно рассматривать как 1/12 куб, или 1/24 ромбический додекаэдр, каждый из которых определяется тремя углами и центром куба.

Связанные косые апейроэдры

Родственная униформа косой апейроэдр существует с тем же расположение вершин, но треугольники и квадрат удалены. Его можно рассматривать как усеченные тетраэдры и усеченные кубы, увеличенные вместе.

Связанные соты

Руническая кубическая

Runcicantellated кубический

Гирированные четырехгранно-октаэдрические соты

Гирированные четырехгранно-октаэдрические соты
Тип	выпуклые однородные соты
Диаграммы Кокстера
Символы Шлефли	ч {4,3,4}: г ч {6,3} ч {∞} с {3,6} ч {∞} с {3^[3]} h {∞}
Клетки	{3,3} {3,4}
Лица	треугольник {3}
Фигура вершины	треугольная ортобикупола G3.4.3.4
Космическая группа	P63/ ммс (194) [3,6,2^+,∞]
Двойной	трапеции-ромбические додекаэдрические соты
Характеристики	вершинно-транзитивный

В спиральные четырехгранно-октаэдрические соты или же спиральные чередующиеся кубические соты заполняет пространство мозаика (или же соты ) в Евклидово 3-пространство состоит из октаэдры и тетраэдры в соотношении 1: 2.

это вершинно-однородный с 8 тетраэдрами и 6 октаэдрами вокруг каждой вершины.

Это не так однотонный. Все ребра имеют 2 тетраэдра и 2 октаэдра, но некоторые чередуются, а некоторые парные.

Видно как отражающие слои этого слоя соты:

Строительство по вращению

Это менее симметричная версия другой соты, тетраэдрическо-октаэдрической соты, в которой каждое ребро окружено чередующимися тетраэдрами и октаэдрами. Обе можно рассматривать как состоящие из слоев толщиной в одну ячейку, внутри которых эти два вида ячеек строго чередуются. Поскольку грани на плоскостях, разделяющих эти слои, образуют правильный узор из треугольников, соседние слои могут быть размещены так, чтобы каждый октаэдр в одном слое встречался с тетраэдром в следующем слое, или же так что каждая ячейка встречает ячейку своего вида (таким образом, граница слоя становится отражение самолет). Последняя форма называется вращающийся.

Фигура вершины называется треугольная ортобикупола, по сравнению с тетраэдрально-октаэдрическими сотами, у которых фигура вершины кубооктаэдр в более низкой симметрии называется треугольная гиробикупола, поэтому префикс гироскопа используется наоборот.

Фигуры вершин

Соты	Гират тет-окт	Светоотражающий тет-окт
Изображение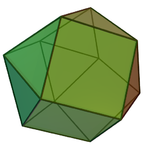
Имя	треугольная ортобикупола	треугольная гиробикупола
Фигура вершины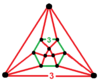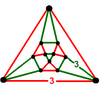
Симметрия	D3ч, заказ 12	D3D, заказ 12 (Oчас, заказ 48)

Строительство чередованием

Фигура вершины с неплоской 3.3.3.3 конфигурация вершины для треугольных бипирамид

Геометрия также может быть построена с помощью чередование операция применяется к шестиугольные призматические соты. В шестиугольная призма клетки становятся октаэдры и пустоты создают треугольные бипирамиды которые можно разделить на пары тетраэдры этой соты. Эти соты с бипирамидами называют дитетраэдрально-восьмигранные соты. Есть 3 Диаграммы Кокстера-Дынкина, который можно увидеть как 1, 2 или 3 цвета октаэдров:

1. 
2. 
3. 

Гиро-удлиненные чередующиеся кубические соты

Гиро-удлиненные чередующиеся кубические соты
Тип	Равномерные соты
Символ Шлефли	h {4,3,4}: ge {3,6} ч1{∞}
Диаграмма Кокстера
Клетки	{3,3} {3,4} (3.4.4)
Лица	треугольник {3} квадрат {4}
Фигура вершины
Космическая группа	P63/ ммс (194) [3,6,2^+,∞]
Характеристики	вершинно-транзитивный

В гиродлинные чередующиеся кубические соты или же удлиненно-треугольная антипризматическая клетчатка заполняет пространство мозаика (или же соты ) в Евклидово 3-пространство. Он состоит из октаэдры, треугольные призмы, и тетраэдры в соотношении 1: 2: 2.

Он вершинно-транзитивный с 3 октаэдрами, 4 тетраэдрами, 6 треугольными призмами вокруг каждой вершины.

Это один из 28 выпуклые однородные соты.

В удлиненные чередующиеся кубические соты имеет одинаковое расположение ячеек в каждой вершине, но общее расположение отличается. в удлиненный форма, каждая призма встречается с тетраэдром на одной из своих треугольных граней и октаэдром на другой; в гиро-удлиненный формы, призма встречается с такими же дельтаэдр на каждом конце.

Удлиненные чередующиеся кубические соты

Удлиненные чередующиеся кубические соты
Тип	Равномерные соты
Символ Шлефли	h {4,3,4}: e {3,6} г1{∞}
Клетки	{3,3} {3,4} (3.4.4)
Лица	треугольник {3} квадрат {4}
Фигура вершины	треугольный купол соединен с равнобедренным шестиугольная пирамида
Группа симметрии	[6,(3,2^+,∞,2^+)] ?
Характеристики	вершинно-транзитивный

В удлиненные чередующиеся кубические соты или же удлиненная треугольная гиропризматическая клетчатка заполняет пространство мозаика (или же соты ) в Евклидово 3-пространство. Он состоит из октаэдры, треугольные призмы, и тетраэдры в соотношении 1: 2: 2.

Он вершинно-транзитивный с 3 октаэдрами, 4 тетраэдрами, 6 треугольными призмами вокруг каждой вершины. Каждая призма встречается с октаэдром на одном конце и тетраэдром на другом.

Это один из 28 выпуклые однородные соты.

Оно имеет вращающийся форма называется гиродлинные чередующиеся кубические соты с одинаковым расположением ячеек в каждой вершине.

Смотрите также

• Архитектурная и катоптическая мозаика
• Кубические соты
• Космическая рамка

Примечания

1. Для перекрестных ссылок они даются с индексами списков от Андреини (1-22), Уильямса (1-2,9-19), Джонсона (11-19, 21-25, 31-34, 41-49, 51- 52, 61-65) и Грюнбаум (1-28).
2. http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/D3.html
3. http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/A3.html
4. Конвей (1998), стр. 119
5. http://www.math.rwth-aachen.de/~Gabriele.Nebe/LATTICES/Ds3.html
6. Конвей (1998), стр. 120
7. Конвей (1998), стр. 466
8. [1], OEIS последовательность A000029 6-1 случаев, пропуская один с нулевыми отметками

Рекомендации

• Джон Х. Конвей, Хайди Берджель, Хаим Гудман-Штраус, (2008) Симметрии вещей, ISBN  978-1-56881-220-5 (Глава 21, Именование архимедовых и каталонских многогранников и плиток, Архитектурные и катоптрические мозаики, стр. 292-298, включает все непризматические формы)
• Георгий Ольшевский, Однородные паноплоидные тетракомбы, Рукопись (2006) (Полный список из 11 выпуклых однородных мозаик, 28 выпуклых однородных сот и 143 выпуклых однородных тетракомб)
• Бранко Грюнбаум, Равномерные мозаики трехмерного пространства. Геомбинаторика 4(1994), 49 - 56.
• Норман Джонсон Равномерные многогранники, Рукопись (1991)
• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN  0-486-23729-X.
• Кричлоу, Кит (1970). Заказ в космосе: справочник по дизайну. Викинг Пресс. ISBN  0-500-34033-1.
• Калейдоскопы: Избранные произведения Х.С.М. Coxeter, под редакцией Ф. Артура Шерка, Питера Макмаллена, Энтони С. Томпсона, Асии Ивика Вайса, публикации Wiley-Interscience, 1995, ISBN  978-0-471-01003-6 [2]
  • (Документ 22) Х.С.М. Кокстер, Регулярные и полурегулярные многогранники I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Однородные заполнители пространств)
  • (Документ 24) Х.С.М. Кокстер, Правильные и полурегулярные многогранники III, [Math. Zeit. 200 (1988) 3-45]
• А. Андреини, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (О правильных и полуправильных сетях многогранников и соответствующих коррелятивных сетях), Mem. Итальянское общество науки, сер. 3, 14 (1905) 75–129.
• Д. М. Ю. Соммервиль, Введение в геометрию п Размеры. Нью-Йорк, Э. П. Даттон, 1930. 196 стр. (Dover Publications edition, 1958) Глава X: Правильные многогранники
• Конвей Дж. Х., Слоан Нью-Джерси (1998). Сферические упаковки, решетки и группы (3-е изд.). ISBN  0-387-98585-9.

внешняя ссылка

• Архитектурный проект, выполненный с использованием тетраэдров и правильных квадратов пирамид (2003 г.)
• Клитцинг, Ричард. "3D евклидовы соты x3o3o * b4o - октет - O21".
• Однородные соты в 3-м пространстве: 11 октетов

v т е Фундаментальный выпуклый обычный и однородные соты в размерах 2-9
Космос	Семья	${\displaystyle {\tilde {A}}_{n-1}}$	${\displaystyle {\tilde {C}}_{n-1}}$	${\displaystyle {\tilde {B}}_{n-1}}$	${\displaystyle {\tilde {D}}_{n-1}}$	${\displaystyle {\tilde {G}}_{2}}$ / ${\displaystyle {\tilde {F}}_{4}}$ / ${\displaystyle {\tilde {E}}_{n-1}}$
E^2	Равномерная черепица	{3^[3]}	δ3	hδ3	qδ3	Шестиугольный
E^3	Равномерно выпуклые соты	{3^[4]}	δ4	hδ4	qδ4
E^4	Равномерные 4-соты	{3^[5]}	δ5	hδ5	qδ5	24-ячеечные соты
E^5	Равномерные 5-соты	{3^[6]}	δ6	hδ6	qδ6
E^6	Равномерные 6-соты	{3^[7]}	δ7	hδ7	qδ7	222
E^7	Равномерные 7-соты	{3^[8]}	δ8	hδ8	qδ8	133 • 331
E^8	Равномерные 8-соты	{3^[9]}	δ9	hδ9	qδ9	152 • 251 • 521
E^9	Равномерные 9-соты	{3^[10]}	δ10	hδ10	qδ10
Eп-1	Униформа (п-1)-соты	{3^[n]}	δп	hδп	qδп	1k2 • 2k1 • k21