Квадратная пирамида - Square pyramid

Квадратная пирамида
Тип	Джонсон J92 – J1 – J2
Лица	4 треугольники 1 квадрат
Края	8
Вершины	5
Конфигурация вершины	4(3^2.4) (3^4)
Символ Шлефли	( ) ∨ {4}
Группа симметрии	C4в, [4], (*44)
Группа вращения	C4, [4]^+, (44)
Двойной многогранник	себя
Характеристики	выпуклый
Сеть

3D модель квадратной пирамиды

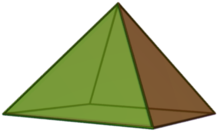
В геометрия, а квадратная пирамида это пирамида иметь квадрат основание. Если вершина находится перпендикулярно к центру квадрата, это правая квадратная пирамида, и имеет C_4в симметрия. Если все ребра равны, это равносторонняя квадратная пирамида,^[1] Джонсон солид J₁.

Общая квадратная пирамида

Возможно наклонная квадратная пирамида с длиной основания л и перпендикулярная высота час имеет объем:

${\displaystyle V={\frac {1}{3}}l^{2}h}$.

Правая квадратная пирамида

В прямоугольной пирамиде все боковые стороны имеют одинаковую длину, а стороны, кроме основания, совпадают. равнобедренные треугольники.

Правая квадратная пирамида с базовой длиной л и высота час имеет площадь поверхности и объем:

${\displaystyle A=l^{2}+l{\sqrt {l^{2}+(2h)^{2}}}}$

${\displaystyle V={\frac {1}{3}}l^{2}h}$.

Длина бокового края составляет:

${\displaystyle {\sqrt {h^{2}+{{l^{2}} \over {2}}}}}$,

а наклонная высота составляет:

${\displaystyle {\sqrt {h^{2}+{{l^{2}} \over {4}}}}}$.

В двугранные углы находятся:

между основанием и бортиком: ${\displaystyle \arctan \left({{2\,h} \over {l}}\right)}$;

между двумя сторонами: ${\displaystyle \arccos \left({{-l^{2}} \over {l^{2}+4\,h^{2}}}\right)}$.

Равносторонняя квадратная пирамида, тело Джонсона J₁

Если все ребра имеют одинаковую длину, то стороны равны равносторонние треугольники, а пирамида представляет собой равностороннюю квадратную пирамиду, Джонсон солид J₁.

Квадратная пирамида Джонсона может быть охарактеризована одним параметром длины ребра л.

Высота час (от середины квадрата до вершины) площадь поверхности А (включая все пять граней), а объем V равносторонней квадратной пирамиды бывают:

${\displaystyle h={\frac {1}{\sqrt {2}}}l}$

${\displaystyle A=(1+{\sqrt {3}})l^{2}}$

${\displaystyle V={\frac {\sqrt {2}}{6}}l^{3}.}$

Двугранные углы равносторонней квадратной пирамиды равны:

• Между основанием и бортиком:

${\displaystyle \arctan {{\biggl (}{\sqrt {2}}{\biggl )}}\approx 54.73561^{\circ }.}$

• Между двумя (соседними) сторонами:

${\displaystyle \arccos {\biggl (}{-1 \over 3}{\biggl )}\approx 109.47122^{\circ }.}$

График

Квадратную пирамиду можно представить График колеса W₅.

Связанные многогранники и соты

Правильные пирамиды
Дигональный	Треугольная	Квадрат	Пятиугольный	Шестиугольный	Семиугольный	Восьмиугольный	Эннеагональный	Десятиугольный ...
Неправильный	Обычный	Равносторонний		Равнобедренный

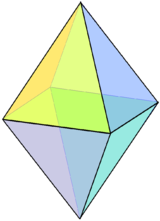
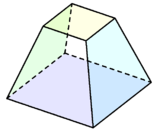
Обычный октаэдр можно считать квадратным бипирамида, то есть две квадратные пирамиды Джонсона, соединенные основанием с основанием.	В тетракис шестигранник может быть построен из куб с короткими квадратными пирамидами, добавленными к каждой грани.	Квадрат усеченный представляет собой квадратную пирамиду с усеченной вершиной.

Квадратные пирамиды заполнить пространство тетраэдры, усеченные кубики или же кубооктаэдр.^[2]

Двойной многогранник

Квадратная пирамида топологически самодвойственный многогранник. Длина двух кромок различается из-за полярное возвратно-поступательное движение.

Двойная квадратная пирамида	Чистая двойная

Рекомендации

1. Франц Хосевар, Твердая геометрия, 1903, п. 44
2. http://w Woodenpolyhedra.web.fc2.com/JohnsonHoneycomb.pdf

внешняя ссылка

• Эрик В. Вайсштейн, Квадратная пирамида (Джонсон солид ) в MathWorld.
• Вайсштейн, Эрик В. «Колесный график». MathWorld.
• Квадратная пирамида - Интерактивная модель многогранника
• Многогранники виртуальной реальности www.georgehart.com: Энциклопедия многогранников (VRML модель )