Икосододекаэдр - Icosidodecahedron - Wikipedia

Икосододекаэдр
(Нажмите здесь, чтобы повернуть модель)
Тип	Архимедово твердое тело Равномерный многогранник
Элементы	F = 32, E = 60, V = 30 (χ = 2)
Лица по сторонам	20{3}+12{5}
Обозначение Конвея	объявление
Символы Шлефли	г {5,3}
	т1{5,3}
Символ Wythoff	2 | 3 5
Диаграмма Кокстера
Группа симметрии	ячас, H3, [5,3], (* 532), заказ 120
Группа вращения	я, [5,3]^+, (532), заказ 60
Двугранный угол	142.62° ${\displaystyle \cos ^{-1}\left(-{\sqrt {{\frac {1}{15}}\left(5+2{\sqrt {5}}\right)}}\right)}$
Рекомендации	U24, C28, W12
Характеристики	Полурегулярный выпуклый квазирегулярный
Цветные лица	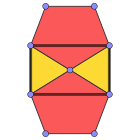3.5.3.5 (Фигура вершины )
Ромбический триаконтаэдр (двойственный многогранник )	Сеть

3D модель икосододекаэдра

В геометрия, икосододекаэдр это многогранник с двадцатью (icosi) треугольными гранями и двенадцатью (dodeca) пятиугольными гранями. Икосододекаэдр имеет 30 идентичных вершин, в каждом из которых встречаются два треугольника и два пятиугольника, а также 60 идентичных ребер, каждое из которых отделяет треугольник от пятиугольника. Таким образом, это один из Архимедовы тела и, в частности, квазирегулярный многогранник.

Геометрия

Икосододекаэдр обладает симметрией икосаэдра, и его первый звездчатость это соединение додекаэдр и его двойная икосаэдр, причем вершины икосододекаэдра расположены в серединах ребер каждого из них.

Его двойственный многогранник это ромбический триаконтаэдр. Икосододекаэдр можно разделить по любой из шести плоскостей, образуя пару пятиугольные ротонды, которые принадлежат к Твердые тела Джонсона.

Икосододекаэдр можно считать пятиугольная гиробиротонда, как комбинация двух ротонды (сравнивать пятиугольная ортобиротонда, один из Твердые тела Джонсона ). В таком виде его симметрия D_5d, [10,2⁺], (2 * 5), порядок 20.

В каркасная фигура икосододекаэдра состоит из шести плоские правильные декагоны, встречающиеся попарно в каждой из 30 вершин.

Икосододекаэдр имеет 6 центральных декагоны. Спроецированные в сферу, они определяют 6 большие круги. Бакминстер Фуллер использовал эти 6 больших кругов вместе с 15 и 10 другими в двух других многогранниках, чтобы определить его 31 большой круг сферического икосаэдра.

Декартовы координаты

Удобный Декартовы координаты для вершин икосододекаэдра с единичными ребрами задаются даже перестановки из:^[1]

• (0, 0, ±φ)
• (±1/2, ±φ/2, ±φ²/2)

куда φ это Золотое сечение, 1 + √5/2.

Ортогональные проекции

Икосододекаэдр имеет четыре особых ортогональные проекции с центром на вершине, ребре, треугольной грани и пятиугольной грани. Последние два соответствуют букве A₂ и H₂ Самолеты Кокстера.

Ортогональные проекции

В центре	Вершина	Край	Лицо Треугольник	Лицо Пентагон
Твердый
Каркас
Проективный симметрия	[2]	[2]	[6]	[10]
Двойной

Площадь и объем поверхности

Площадь поверхности А и объем V икосододекаэдра длины ребра а находятся:

${\displaystyle {\begin{aligned}A&=\left(5{\sqrt {3}}+3{\sqrt {5}}{\sqrt {3+4\varphi }}\right)a^{2}&&=\left(5{\sqrt {3}}+3{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}&&\approx 29.3059828a^{2}\\V&={\frac {14+17\varphi }{3}}a^{3}&&={\frac {45+17{\sqrt {5}}}{6}}a^{3}&&\approx 13.8355259a^{3}.\end{aligned}}}$

Сферическая черепица

60 ребер образуют 6 декагоны соответствующий большие круги в сферической плитке.

Икосододекаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.

	Пентагон -центрированный	Треугольник -центрированный
Ортографическая проекция	Стереографические проекции

Ортографические проекции
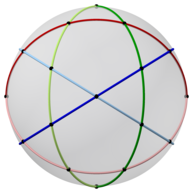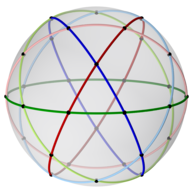2-кратные, 3-кратные и 5-кратные оси симметрии

Связанные многогранники

Икосододекаэдр - это исправленный додекаэдр а также исправленный икосаэдр, существующее как усечение по всей кромке между этими правильными телами.

Икосододекаэдр содержит 12 пятиугольников додекаэдр и 20 треугольников икосаэдр:

Семейство однородных икосаэдрических многогранников
Симметрия: [5,3], (*532)							[5,3]^+, (532)
{5,3}	т {5,3}	г {5,3}	т {3,5}	{3,5}	рр {5,3}	tr {5,3}	ср {5,3}
Двойники к однородным многогранникам
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Икосододекаэдр существует в последовательности симметрий квазирегулярных многогранников и мозаик с конфигурации вершин (3.п)², переходя от мозаики сферы к евклидовой плоскости и к гиперболической плоскости. С орбифолдная запись симметрия *п32 все эти мозаики Wythoff Construction в пределах фундаментальная область симметрии, с образующими точками в правом углу области.^[2][3]

*п32 орбифолдные симметрии квазирегулярных мозаик: (3.п)^2
Строительство	Сферический			Евклидово	Гиперболический
	*332	*432	*532	*632	*732	*832...	*∞32
Квазирегулярный цифры
Вершина	(3.3)^2	(3.4)^2	(3.5)^2	(3.6)^2	(3.7)^2	(3.8)^2	(3.∞)^2

*5п2 мутации симметрии квазирегулярных мозаик: (5.n)^2 v т е
Симметрия *5п2 [n, 5]	Сферический	Гиперболический					Паракомпакт	Некомпактный
	*352 [3,5]	*452 [4,5]	*552 [5,5]	*652 [6,5]	*752 [7,5]	*852 [8,5]...	*∞52 [∞,5]	[пя, 5]
Цифры
Конфиг.	(5.3)^2	(5.4)^2	(5.5)^2	(5.6)^2	(5.7)^2	(5.8)^2	(5.∞)^2	(5.пя)^2
Ромбический цифры
Конфиг.	V (5,3)^2	V (5,4)^2	V (5.5)^2	V (5,6)^2	V (5,7)^2	V (5,8)^2	V (5.∞)^2	V (5.∞)^2

Рассечение

Икосододекаэдр связан с Джонсон солид называется пятиугольная ортобиротонда создан двумя пятиугольная ротонда связаны как зеркальные изображения. В икосододекаэдр поэтому можно назвать пятиугольная гиробиротонда с вращением между верхней и нижней половинами.

(Рассечение)

Икосододекаэдр (пятиугольная гиробиротонда) Пятиугольная ортобиротонда Пятиугольная ротонда

Связанные многогранники

Икосидодекаэдр в усеченном кубе

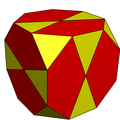
В усеченный куб можно превратить в икосододекаэдр, разделив восьмиугольники на два пятиугольника и два треугольника. Она имеет пиритоэдрическая симметрия.

8 однородные звездные многогранники разделять то же самое расположение вершин. Двое из них имеют одинаковые расположение кромок: the малый икосигемидодекаэдр (имеющий общие треугольные грани), а малый додекагемидодекаэдр (имеющий общие пятиугольные грани). Расположение вершин также совпадает с соединения из пять октаэдров и из пять тетрагемигексаэдров.

Икосододекаэдр	Малый икосигемидодекаэдр	Малый додекагемидодекаэдр
Большой икосододекаэдр	Большой додекагемидодекаэдр	Большой икосигемидодекаэдр
Додекадодекаэдр	Малый додекагемикосаэдр	Большой додекагемикосаэдр
Соединение пяти октаэдров	Соединение пяти тетрагемигексаэдров

Родственная полихора

В четырехмерной геометрии икосододекаэдр появляется в обычный 600 ячеек как экваториальный срез, который принадлежит первому вершине прохождения 600-ячеек через трехмерное пространство. Другими словами: 30 вершин 600-ячейки, которые лежат на расстоянии 90 градусов по дуге от ее описанной гиперсфера из пары противоположных вершин - вершины икосододекаэдра. Каркас 600-элементного блока состоит из 72 плоских правильных декагонов. Шесть из них являются экваториальными декагонами к паре противоположных вершин. Это в точности шесть декагонов, которые образуют проволочную рамку икосододекаэдра.

Икосидодекаэдрический граф

Икосидодекаэдрический граф
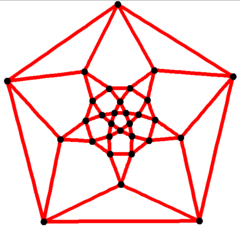5-кратная симметрия Диаграмма Шлегеля
Вершины	30
Края	60
Автоморфизмы	120
Характеристики	Граф четвертого порядка, Гамильтониан, обычный
Таблица графиков и параметров

в математический поле теория графов, а икосододекаэдрический граф это граф вершин и ребер икосододекаэдра, один из Архимедовы тела. Имеет 30 вершины и 60 ребер, а это граф четвертой степени Архимедов граф.^[4]

Мелочи

В Вселенная Звездного Пути, Вулканская логическая игра Кал-То имеет цель создать голографический икосододекаэдр.

В Не те звездыВ первой книге серии «Аксиома» Тима Пратта, по обе стороны от Елены находится машина икосододекаэдра. [Мягкая обложка, стр. 336]

В Сфера Хобермана - икосадодекаэдр.

Смотрите также

• Кубооктаэдр
• Большой усеченный икосододекаэдр
• Икосаэдр
• Ромбикосододекаэдр
• Усеченный икосододекаэдр

Примечания

1. Вайсштейн, Эрик В. «Икосаэдрическая группа». MathWorld.
2. Coxeter Правильные многогранники, Третье издание, (1973), Дуврское издание, ISBN  0-486-61480-8 (Глава V: Калейдоскоп, Раздел: 5.7 Конструкция Витхоффа)
3. Двумерные мутации симметрии Дэниел Хьюсон
4. Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, п. 269

Рекомендации

• Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN  0-486-23729-X. (Раздел 3-9)
• Кромвель, П. (1997). Многогранники. Великобритания: Кембридж. стр. 79–86 Архимедовы тела. ISBN  0-521-55432-2.

внешняя ссылка

• Эрик В. Вайсштейн, Икосододекаэдр (Архимедово твердое тело ) в MathWorld.
• Клитцинг, Ричард. "3D выпуклые равномерные многогранники o3x5o - id".
• Редактируемая печатная сетка икосододекаэдра с интерактивным трехмерным изображением
• Равномерные многогранники
• Многогранники виртуальной реальности Энциклопедия многогранников