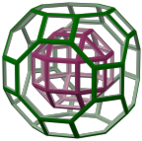
Усеченный кубооктаэдр - Truncated cuboctahedron

Усеченный кубооктаэдр
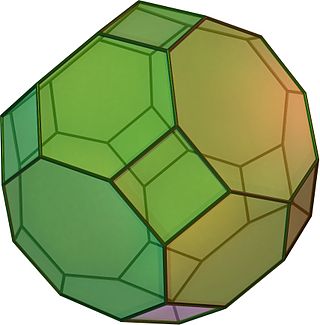(Нажмите здесь, чтобы повернуть модель)
Тип	Архимедово твердое тело Равномерный многогранник
Элементы	F = 26, E = 72, V = 48 (χ = 2)
Лица по сторонам	12{4}+8{6}+6{8}
Обозначение Конвея	bC или taC
Символы Шлефли	tr {4,3} или ${\displaystyle t{\begin{Bmatrix}4\\3\end{Bmatrix}}}$
	т0,1,2{4,3}
Символ Wythoff	2 3 4 |
Диаграмма Кокстера
Группа симметрии	Очас, B3, [4,3], (* 432), порядок 48
Группа вращения	О, [4,3]^+, (432), заказ 24
Двугранный угол	4-6: arccos (-√6/3) = 144°44′08″ 4-8: arccos (-√2/3) = 135° 6-8: arccos (-√3/3) = 125°15′51″
Рекомендации	U11, C23, W15
Характеристики	Полурегулярный выпуклый зоноэдр
Цветные лица	4.6.8 (Фигура вершины )
Додекаэдр Дисдякиса (двойственный многогранник )	Сеть

В геометрия, то усеченный кубооктаэдр является Архимедово твердое тело, названный Кеплером усечение из кубооктаэдр. Имеет 12 квадрат лиц, 8 обычных шестиугольник лиц, 6 обычных восьмиугольный грани, 48 вершин и 72 ребра. Поскольку каждая его грань имеет точечная симметрия (эквивалентно 180 ° вращающийся симметрии) усеченный кубооктаэдр представляет собой зоноэдр. Усеченный кубооктаэдр может мозаика с восьмиугольная призма.

Имена

Название усеченный кубооктаэдр, первоначально предоставленный Иоганн Кеплер, вводит в заблуждение. Фактический усечение из кубооктаэдр имеет прямоугольники вместо квадраты. Этот неоднородный многогранник топологически эквивалент архимедова твердого тела. Альтернативные взаимозаменяемые имена: Усеченный кубооктаэдр (Иоганн Кеплер ) Ромбоусеченный кубооктаэдр (Магнус Веннингер[1]) Большой ромбокубооктаэдр (Роберт Уильямс[2]) Большой ромбокубооктаэдр (Питер Кромвель[3]) Усеченный куб или же усеченный куб (Норман Джонсон ) Скошенный куб (Обозначения многогранника Конвея )

Кубооктаэдр и его усечение

Существует невыпуклый однородный многогранник с похожим названием невыпуклый большой ромбокубооктаэдр.

Декартовы координаты

В Декартовы координаты все вершины усеченного кубооктаэдра с длиной ребра 2 и центром в начале координат равны перестановки из:

(±1, ±(1 + √2), ±(1 + 2√2))

Площадь и объем

Площадь А и объем V усеченного кубооктаэдра длины ребра а находятся:

${\displaystyle {\begin{aligned}A&=12\left(2+{\sqrt {2}}+{\sqrt {3}}\right)a^{2}&&\approx 61.755\,1724a^{2}\\V&=\left(22+14{\sqrt {2}}\right)a^{3}&&\approx 41.798\,9899a^{3}.\end{aligned}}}$

Рассечение

Усеченный кубооктаэдр - это выпуклый корпус из ромбокубооктаэдр с кубиками над его 12 квадратами на 2-кратных осях симметрии. Остальное пространство можно разделить на 6 квадратные купола ниже восьмиугольников и 8 треугольные купола ниже шестиугольников.

Рассеченный усеченный кубооктаэдр может создать род 5, 7 или 11. Тороид Стюарта удалив центральный ромбокубооктаэдр и квадратные, треугольные или 12 кубов соответственно. Многие другие тороиды с более низкой симметрией также могут быть построены путем удаления подмножества этих рассеченных компонентов. Например, удаление половины треугольных куполов создает тор рода 3, который (если они правильно выбраны) имеет тетраэдрическую симметрию.^[4][5]

Тороиды Стюарта
Род 3	Род 5	Род 7	Род 11

Равномерная окраска

Здесь только один равномерная окраска граней этого многогранника по одному цвету для каждого типа граней.

2-х однородная окраска, с тетраэдрическая симметрия, существует с попеременно окрашенными шестиугольниками.

Ортогональные проекции

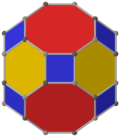
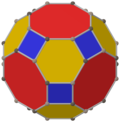
У усеченного кубооктаэдра есть два особых ортогональные проекции в А₂ и B₂ Самолеты Кокстера с проективной симметрией [6] и [8], а многочисленные [2] симметрии могут быть построены из различных спроецированных плоскостей относительно элементов многогранника.

Ортогональные проекции

В центре	Вершина	Край 4-6	Край 4-8	Край 6-8	Лицо нормальное 4-6
Изображение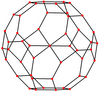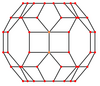
Проективный симметрия	[2]^+	[2]	[2]	[2]	[2]
В центре	Лицо нормальное Квадрат	Лицо нормальное Восьмиугольник	Лицо Квадрат	Лицо Шестиугольник	Лицо Восьмиугольник
Изображение
Проективный симметрия	[2]	[2]	[2]	[6]	[4]

Сферическая черепица

Усеченный кубооктаэдр также можно представить в виде сферическая черепица, и проецируется на плоскость через стереографическая проекция. Эта проекция конформный, сохраняя углы, но не площади или длины. Прямые на сфере проецируются как дуги окружности на плоскость.

Ортогональная проекция	квадрат -центрированный	шестиугольник -центрированный	восьмиугольник -центрированный
	Стереографические проекции

Полная октаэдрическая группа

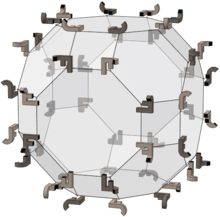
Как и многие другие твердые тела, усеченный октаэдр имеет полный октаэдрическая симметрия - но его связь с полной октаэдрической группой более тесная: его 48 вершин соответствуют элементам группы, и каждая грань его двойной это фундаментальная область группы.

На изображении справа показаны 48 перестановок в группе, примененной к объекту-примеру (а именно, к легкому соединению JF слева). 24 светлых элемента - это вращения, а темные - их отражения.

Ребра тела соответствуют 9 отражениям в группе:

• Те между восьмиугольниками и квадратами соответствуют трем отражениям между противоположными восьмиугольниками.
• Края шестиугольника соответствуют 6 отражениям между противоположными квадратами.
• (Между противоположными шестиугольниками нет отражений.)

Подгруппы соответствуют телам, которые разделяют соответствующие вершины усеченного октаэдра.
Например. 3 подгруппы по 24 элемента соответствуют неравномерному курносый куб с киральной октаэдрической симметрией неоднородная усеченный октаэдр с полная тетраэдрическая симметрия и неоднородный ромбокубооктаэдр с пиритоэдрическая симметрия (в кантик курносый октаэдр ).
Единственная подгруппа из 12 элементов - это переменная группа А₄. Это соответствует неравномерному икосаэдр с хиральная тетраэдрическая симметрия.

Подгруппы и соответствующие твердые тела
все 48 вершин	24 вершины			12 вершин

Связанные многогранники

Тетраэдр-бабочка и куб содержат две трапециевидные грани вместо квадрата.[6]

Усеченный кубооктаэдр является одним из семейства однородных многогранников, связанных с кубом и правильным октаэдром.

Однородные октаэдрические многогранники
Симметрия: [4,3], (*432)							[4,3]^+ (432)	[1^+,4,3] = [3,3] (*332)		[3^+,4] (3*2)
{4,3}	т {4,3}	г {4,3} г {3^1,1}	т {3,4} т {3^1,1}	{3,4} {3^1,1}	рр {4,3} s2{3,4}	tr {4,3}	sr {4,3}	ч {4,3} {3,3}	час2{4,3} т {3,3}	с {3,4} с {3^1,1}
		=	=	=				= или же	= или же	=
Двойники к однородным многогранникам
V4^3	V3.8^2	V (3,4)^2	V4.6^2	V3^4	V3.4^3	V4.6.8	V3^4.4	V3^3	V3.6^2	V3^5

Этот многогранник можно рассматривать как член последовательности однородных узоров с конфигурация вершины (4.6.2п) и Диаграмма Кокстера-Дынкина . За п <6, членами последовательности являются всесторонне усеченный многогранники (зоноэдры ), показанные ниже в виде сферических мозаик. За п <6, это мозаики гиперболической плоскости, начиная с усеченная трехгептагональная черепица.

*п32 мутации симметрии полностью усеченных мозаик: 4.6.2n [ v т е ]
Сим. *п32 [п,3]	Сферический				Евклид.	Компактная гиперболия.		Paraco.	Некомпактный гиперболический
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]	[3i, 3]
Цифры
Конфиг.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Конфиг.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

*п42 мутации симметрии полностью усеченных мозаик: 4.8.2n [ v т е ]
Симметрия *п42 [n, 4]	Сферический		Евклидово	Компактный гиперболический				Paracomp.
	*242 [2,4]	*342 [3,4]	*442 [4,4]	*542 [5,4]	*642 [6,4]	*742 [7,4]	*842 [8,4]...	*∞42 [∞,4]
Усеченный фигура	4.8.4	4.8.6	4.8.8	4.8.10	4.8.12	4.8.14	4.8.16	4.8.∞
Усеченный двойники	V4.8.4	V4.8.6	V4.8.8	V4.8.10	V4.8.12	V4.8.14	V4.8.16	V4.8.∞

Это первый из ряда усеченных гиперкубов:

Многоугольник Петри прогнозы

Усеченный кубооктаэдр	Усеченный тессеракт	Усеченный 5-куб	Усеченный 6-куб	Cantitruncated 7-куб	Усеченный 8-куб

Усеченный кубооктаэдрический граф

Усеченный кубооктаэдрический граф
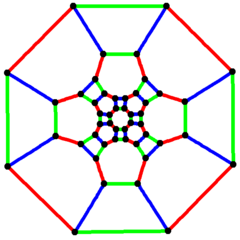4-х кратная симметрия
Вершины	48
Края	72
Автоморфизмы	48
Хроматическое число	2
Характеристики	Кубический, Гамильтониан, обычный, нулевой симметричный
Таблица графиков и параметров

в математический поле теория графов, а усеченный кубооктаэдрический граф (или же большой ромбкубооктаэдрический граф) это граф вершин и ребер усеченного кубооктаэдра, один из Архимедовы тела. Имеет 48 вершины и 72 ребра, и является нулевой симметричный и кубический Архимедов граф.^[7]

Смотрите также

• Куб
• Кубооктаэдр
• Октаэдр
• Усеченный икосододекаэдр
• Усеченный октаэдр - усеченный тетратетраэдр

Рекомендации

1. Веннингер, Магнус (1974), Модели многогранников, Издательство Кембриджского университета, ISBN  978-0-521-09859-5, МИСТЕР  0467493 (Модель 15, стр.29)
2. Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN  0-486-23729-X. (Раздел 3-9, стр. 82)
3. Cromwell, P .; Многогранники, CUP hbk (1997), pbk. (1999). (стр.82)
4. Б. М. Стюарт, Приключения среди тороидов (1970) ISBN  978-0-686-11936-4
5. Доски, Алекс. "Приключения среди тороидов - Глава 5 - Простейшие (R) (A) (Q) (T) Тороиды рода p = 1". www.doskey.com.
6. Симметроэдры: многогранники из симметричного размещения правильных многоугольников Крейг С. Каплан
7. Читать, R.C .; Уилсон, Р. Дж. (1998), Атлас графиков, Oxford University Press, п. 269

• Кромвель, П. (1997). Многогранники. Великобритания: Кембридж. стр. 79–86 Архимедовы тела. ISBN  0-521-55432-2.

внешняя ссылка

• Эрик В. Вайсштейн, Большой ромбокубооктаэдр (Архимедово твердое тело ) в MathWorld.
  • Вайсштейн, Эрик В. «Большой ромбокубооктаэдрический граф». MathWorld.
• Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3x4x - girco".
• Редактируемая печатная сетка усеченного кубооктаэдра с интерактивным трехмерным изображением
• Равномерные многогранники
• Многогранники виртуальной реальности Энциклопедия многогранников
• большой ромбокубооктаэдр: бумажные полоски для плетения