Гиро-удлиненная бипирамида - Gyroelongated bipyramid - Wikipedia
| Набор гиродлинных бипирамид | |
|---|---|
 Пятиугольная гиродлинная бипирамида - это правильная икосаэдр. | |
| Лица | 4п треугольники |
| Края | 6п |
| Вершины | 2п+2 |
| Группа симметрии | Dпd, [2+,2п], (2*п), порядок 4п |
| Группа вращения | Dп, [2,п]+, (22п), порядок 2п |
| Двойной многогранник | усеченные трапецоэдры |
| Характеристики | выпуклый |
В геометрия, то гиродлинные бипирамиды бесконечный набор многогранники, построенный путем удлинения п-гональный бипирамида вставив п-гональный антипризма между его конгруэнтными половинками.
Формы
Два члена набора могут быть дельтаэдры, то есть построенный полностью из равносторонние треугольники: the гиродлинная квадратная бипирамида, а Джонсон солид, а икосаэдр, а Платоново твердое тело. В гиродлинная треугольная бипирамида может состоять из равносторонних треугольников, но не является дельтаэдром, поскольку имеет компланарные грани, т.е. не является строго выпуклым. С парами треугольников, сливающихся в ромбы, это можно рассматривать как треугольный трапецоэдр. Остальные элементы можно построить из равнобедренных треугольников.
| п | 3 | 4 | 5 | 6 | п |
|---|---|---|---|---|---|
| Тип | Копланарный | Равносторонний | Обычный | Копланарный | |
| Форма | Гироудлиненная треугольная бипирамида | Гиро-удлиненная квадратная бипирамида | Гиро-удлиненная пятиугольная бипирамида (икосаэдр ) | Гиро-удлиненная гексагональная бипирамида | Гиро-удлиненная бипирамида |
| Изображение |  |  |  | 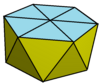 | |
| Лица | 12 | 16 | 20 | 24 | 4п |
| Двойной | Треугольный усеченный трапецоэдр | Квадратный усеченный трапецоэдр | Пятиугольный усеченный трапецоэдр (Додекаэдр ) | Шестиугольный усеченный трапецоэдр | Усеченные трапецоэдры |
Смотрите также
внешняя ссылка
- Обозначение Конвея для многогранников Попробуйте: "kпАп", куда п= 4,5,6 ... пример «k5A5» - икосаэдр.
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |
