Вращение - Rotation

Сфера, вращающаяся (вращающаяся) вокруг оси

А вращение представляет собой круговое движение объекта вокруг центра (или точки) вращения. В геометрическая плоскость вдоль которой происходит вращение, называется плоскость вращения, а воображаемая линия простирающаяся от центра и перпендикулярная плоскости вращения, называется ось вращения (/ˈæksяz/ АК-seez ). Трехмерный объект всегда можно вращать вокруг бесконечного числа осей вращения.

Если ось вращения проходит внутри собственного тела центр массы, то тело называется авторотационный или же прядение, а поверхность пересечения оси можно назвать столб. Вращение вокруг полностью внешней оси, например планета земной шар вокруг солнце, называется вращающийся или же вращающийся по орбите, как правило, когда он производится сила тяжести, а концы оси вращения можно назвать орбитальные полюса.

Математика

Вращение плоской фигуры вокруг точки

Орбита вращения против вращения

Отношения между осью вращения, плоскость орбиты и осевой наклон (для Земли).

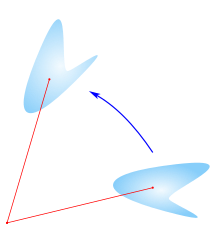
Математически, поворот - это жесткое тело движение, которое, в отличие от перевод, фиксирует точку. Это определение применяется к поворотам как в двух, так и в трех измерениях (на плоскости и в пространстве соответственно).

Все движения твердого тела - это вращения, перемещения или их комбинации.

Вращение - это просто прогрессивная радиальная ориентация к общей точке. Эта общая точка находится внутри оси этого движения. Ось расположена на 90 градусов перпендикулярно плоскости движения. Если ось вращения лежит вне рассматриваемого тела, то говорят, что тело вращается по орбите. Нет принципиальной разницы между «вращением» и «орбитой» или «вращением». Ключевое различие заключается в том, где находится ось вращения, внутри или снаружи рассматриваемого тела. Это различие может быть продемонстрировано как для «твердых», так и для «нежестких» тел.

Если за вращением вокруг точки или оси следует второе вращение вокруг той же точки или оси, получается третье вращение. Обратное (обратный ) вращения также является вращением. Таким образом, вращения вокруг точки / оси образуют группа. Однако вращение вокруг точки или оси и вращение вокруг другой точки / оси может привести к чему-то другому, кроме вращения, например перевод.

Вращения вокруг Икс, у и z топоры называются основные вращения. Вращение вокруг любой оси может быть выполнено вращением вокруг Икс оси с последующим вращением вокруг у оси, а затем вращение вокруг z ось. Иными словами, любое пространственное вращение можно разложить на комбинацию основных вращений.

В динамика полета, то основные вращения известны как рыскание, подача, и рулон (известный как Углы Тейта – Брайана ). Эта терминология также используется в компьютерная графика.

Астрономия

Звездные тропы вызвано Вращение Земли вовремя длинная выдержка камеры время.^[1]

В астрономия, вращение - обычное явление. Звезды, планеты и подобные тела все вращаются на своих осях. Скорость вращения планет Солнечной системы была впервые измерена путем отслеживания визуальных характеристик. Звездное вращение измеряется через Доплеровский сдвиг или отслеживая активные элементы поверхности.

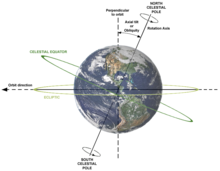
Это вращение вызывает центробежное ускорение в системе отсчета Земли, которая немного противодействует действию гравитации, чем ближе она к экватор. Один из эффектов заключается в том, что объект весит немного меньше на экваторе. Другой - то, что Земля слегка деформирована в сплюснутый сфероид.

Еще одно следствие вращения планеты - это явление прецессия. Как гироскоп, общий эффект - небольшое «колебание» в движении оси планеты. В настоящее время наклон земной шар оси к плоскости ее орбиты (наклон эклиптики ) составляет 23,44 градуса, но этот угол меняется медленно (в течение тысяч лет). (Смотрите также Прецессия равноденствий и Полярная звезда.)

Вращение и революция

В то время как вращение часто используется как синоним вращения, во многих областях, особенно в астрономии и связанных областях, вращение, часто называемое орбитальным вращением для ясности, используется, когда одно тело движется вокруг другого, в то время как вращение используется для обозначения движения вокруг тела. ось. Луны вращаются вокруг своей планеты, планеты вращаются вокруг своей звезды (например, Земля вокруг Солнца); и звезды медленно вращаются вокруг своих галактический центр. Движение компонентов галактики является сложным, но обычно включает в себя компонент вращения.

Ретроградное вращение

Наиболее планеты в нашем Солнечная система, включая земной шар, вращаются в том же направлении, что и солнце. Исключения составляют Венера и Уран. Уран вращается почти на бок относительно своей орбиты. Текущее предположение состоит в том, что Уран начинал с типичной прямой ориентации и был сбит на бок в результате сильного удара в начале своей истории. Можно представить себе Венеру как медленно вращающуюся назад (или «перевернутую»). В карликовая планета Плутон (ранее считавшаяся планетой) аномальна в этом и других отношениях.

Физика

В скорость вращения дается угловая частота (рад / с) или частота (повороты за раз), или период (секунды, дни и т. д.). Скорость изменения угловой частоты - это угловое ускорение (рад / с²), вызванное крутящий момент. Отношение этих двух (насколько тяжело запускать, останавливать или иным образом изменять вращение) определяется момент инерции.

В угловая скорость вектор ( осевой вектор ) также описывает направление оси вращения. Точно так же крутящий момент - это осевой вектор.

Физика вращение вокруг фиксированной оси математически описывается с помощью ось-угол представление вращений. Согласно правило правой руки, направление от наблюдателя связано с вращением по часовой стрелке, а направление к наблюдателю - с вращением против часовой стрелки, как винт.

Космологический принцип

В законы физики в настоящее время считаются инвариантен относительно любого фиксированного вращения. (Хотя кажется, что они меняются при просмотре с вращающейся точки обзора: см. вращающаяся система отсчета.)

В современной физической космологии космологический принцип представление о распределении материи во Вселенной однородный и изотропный если смотреть в достаточно большом масштабе, поскольку ожидается, что силы будут действовать равномерно по всей Вселенной и не будут иметь предпочтительного направления, и, следовательно, не должны вызывать наблюдаемых неоднородностей в крупномасштабной структуре в ходе эволюции поля материи, которое было изначально заложены Большим взрывом.

В частности, для системы, которая ведет себя одинаково независимо от того, как она ориентирована в пространстве, ее Лагранжиан инвариантно относительно вращения. В соответствии с Теорема Нётер, если действие (в интеграл с течением времени своего лагранжиана) физической системы инвариантно относительно вращения, то угловой момент сохраняется.

Вращения Эйлера

Эйлеровы вращения Земли. Внутренний (зеленый), прецессионный (синий) и нутационный (красный)

Вращения Эйлера дают альтернативное описание вращения. Это композиция из трех вращений, определяемых как движение, полученное путем изменения одного из Углы Эйлера оставив два других постоянными. Вращения Эйлера никогда не выражаются в терминах внешней системы отсчета или в терминах совместно движущейся системы координат вращающегося тела, а в виде смеси. Они составляют смешанную систему осей вращения, где первый угол перемещает линия узлов вокруг внешней оси z, второй вращается вокруг линия узлов и третий - собственное вращение вокруг оси, закрепленной в движущемся теле.

Эти вращения называются прецессия, нутация, и собственное вращение.

Динамика полета

Главные оси вращения в пространстве

В динамика полета, главные вращения, описываемые Углы Эйлера выше известны как подача, рулон и рыскание. Период, термин вращение также используется в авиации для обозначения тангажа самолета вверх (нос поднимается вверх), особенно при начале набора высоты после взлета.

Основные вращения имеют преимущество моделирования ряда физических систем, таких как подвесы, и джойстики, поэтому легко визуализируются и представляют собой очень компактный способ хранения вращения. Но их сложно использовать в расчетах, поскольку даже простые операции, такие как объединение поворотов, являются дорогостоящими и страдают от формы карданный замок где углы не могут быть однозначно рассчитаны для определенных поворотов.

Аттракционы

Много аттракционы обеспечить вращение. А колесо обозрения имеет горизонтальную центральную ось и параллельные оси для каждой гондолы, где вращение противоположно, под действием силы тяжести или механически. В результате в любой момент гондола имеет вертикальную ориентацию (не поворачивается), просто переводится. Кончик вектора перемещения описывает круг. А карусель обеспечивает вращение вокруг вертикальной оси. Многие аттракционы предусматривают комбинацию вращений вокруг нескольких осей. В Chair-O-Planes вращение вокруг вертикальной оси обеспечивается механически, а вращение вокруг горизонтальной оси - за счет центростремительная сила. В инверсии американских горок вращение вокруг горизонтальной оси - это один или несколько полных циклов, когда инерция удерживает людей на своих местах.

Спортивный

Вращение шара или другого объекта, обычно называемого вращение, играет важную роль во многих видах спорта, в том числе вершина и обратное вращение в теннис, английский, следить и рисовать в бильярд и пул, кривые шары в бейсбол, спин боулинг в крикет, летающий диск спорт и др. Настольный теннис ракетки производятся с различными характеристиками поверхности, чтобы игрок мог придавать мячу большее или меньшее вращение.

Поворот игрока один или несколько раз вокруг вертикальной оси можно назвать вращение в фигурное катание, кружение (эстафеты или исполнителя) в вертеть дубинкой, или же 360, 540, 720и др. в кататься на сноуборде и т.д. Поворот игрока или исполнителя один или несколько раз вокруг горизонтальной оси можно назвать кувырок, рулон, сальто, heliи др. в гимнастика, водные лыжи, или многие другие виды спорта, или один с половиной, два с половиной, выигрыш (начиная лицом от воды) и т. д. в дайвинг и т. д. Комбинация вертикального и горизонтального вращения (переворот назад на 360 °) называется Мебиус в водные лыжи вольный стиль прыжки.

Вращение игрока вокруг вертикальной оси, обычно от 180 до 360 градусов, можно назвать вращать движение и используется как обманный маневр или маневр уклонения, или в попытке сыграть, передать или получить мяч или шайбу и т. д., или чтобы дать игроку возможность видеть ворота или других игроков. Это часто можно увидеть в хоккей, баскетбол, футбол различных кодов, теннис, так далее.

Фиксированная ось против фиксированной точки

В конечный результат любой последовательности вращений любого объекта в 3D вокруг фиксированной точки всегда эквивалентно вращению вокруг оси. Однако объект может физически вращение в 3D вокруг фиксированной точки по более чем одной оси одновременно, и в этом случае нет единой фиксированной оси вращения - только фиксированная точка. Однако эти два описания можно согласовать - такое физическое движение всегда можно заново описать в терминах единственной оси вращения, при условии, что ориентация этой оси относительно объекта может изменяться от момента к моменту.

Ось 2-х мерного вращения

Двухмерные вращения, в отличие от трехмерных, не имеют оси вращения. Это эквивалентно для линейных преобразований, когда говорится, что нет направления в месте, которое не изменяется при двухмерном вращении, за исключением, конечно, тождества.

Вопрос о существовании такого направления - это вопрос о существовании собственный вектор для матрицы A, представляющей вращение. Каждое двумерное вращение вокруг начала координат на угол ${displaystyle heta}$ в направлении против часовой стрелки может быть довольно просто представлена следующей матрицей:

{displaystyle A = {egin {bmatrix} cos heta & -sin heta sin heta & cos heta end {bmatrix}}}

Стандарт собственное значение решимость приводит к характеристическое уравнение

{displaystyle lambda ^ {2} -2lambda cos heta + 1 = 0}

,

у которого есть

{displaystyle cos heta pm isin heta}

в качестве собственных значений. Следовательно, не существует реального собственного значения всякий раз, когда ${displaystyle cos heta eq pm 1}$ , что означает, что ни один действительный вектор в плоскости не остается неизменным А.

Угол поворота и ось в 3-х измерениях

Зная, что след является инвариантом, угол поворота ${displaystyle alpha}$ для правильной ортогональной матрицы вращения 3x3 ${displaystyle A}$ найден

${displaystyle alpha = cos ^ {- 1} left ({frac {A_ {11} + A_ {22} + A_ {33} -1} {2}} ight)}$

Используя главный арккосинус, эта формула дает угол поворота, удовлетворяющий ${displaystyle 0leq alpha leq 180 ^ {circ}}$ . Соответствующая ось вращения должна быть определена так, чтобы указывать в направлении, ограничивающем угол поворота до 180 градусов. (Это всегда можно сделать, потому что любой поворот более чем на 180 градусов вокруг оси ${displaystyle m}$ всегда можно записать как вращение, имеющее ${displaystyle 0leq alpha leq 180 ^ {circ}}$ если ось заменена на ${displaystyle n = -m}$ .)

Каждое правильное вращение ${displaystyle A}$ в трехмерном пространстве имеет ось вращения, которая определена так, что любой вектор ${displaystyle v}$ который выровнен с осью вращения, вращение не повлияет. Соответственно, ${displaystyle Av = v}$ , поэтому ось вращения соответствует собственному вектору матрицы вращения, связанному с собственным значением, равным 1. Пока угол поворота ${displaystyle alpha}$ отлична от нуля (т.е. вращение не является тождественным тензором), такое направление одно и только одно. Поскольку A имеет только действительные компоненты, существует по крайней мере одно действительное собственное значение, а оставшиеся два собственных значения должны быть комплексно сопряженными друг другу (см. Собственные значения и собственные векторы # Собственные значения и характеристический многочлен ). Зная, что 1 является собственным значением, следует, что оставшиеся два собственных значения являются комплексно сопряженными друг другу, но это не означает, что они являются комплексными - они могут быть действительными с двойной кратностью. В вырожденном случае угла поворота ${displaystyle alpha = 180 ^ {circ}}$ , оставшиеся два собственных значения равны -1. В вырожденном случае нулевого угла поворота матрица вращения является единичной, и все три собственных значения равны 1 (что является единственным случаем, для которого ось вращения произвольна).

Для нахождения оси вращения спектральный анализ не требуется. Если ${displaystyle n}$ обозначает единичный собственный вектор, выровненный с осью вращения, и если ${displaystyle alpha}$ обозначает угол поворота, то можно показать, что ${displaystyle 2sin (alpha) n = {A_ {32} -A_ {23}, A_ {13} -A_ {31}, A_ {21} -A_ {12}}}$ . Следовательно, затрат на анализ собственных значений можно избежать, просто нормализовав этот вектор если он имеет ненулевую величину. С другой стороны, если этот вектор имеет нулевую величину, это означает, что ${displaystyle sin (alpha) = 0}$ . Другими словами, этот вектор будет равен нулю тогда и только тогда, когда угол поворота равен 0 или 180 градусов, и ось вращения может быть назначена в этом случае путем нормализации любого столбца ${displaystyle A + I}$ имеющий ненулевую величину.^[2]

Это обсуждение относится к правильному вращению, и, следовательно, ${displaystyle det A = 1}$ . Любая несобственная ортогональная матрица 3x3 ${displaystyle B}$ можно записать как ${displaystyle B = -A}$ , в котором ${displaystyle A}$ собственно ортогонален. Таким образом, любая неправильная ортогональная матрица 3x3 может быть разложена на собственное вращение (из которого можно найти ось вращения, как описано выше) с последующей инверсией (умножением на -1). Отсюда следует, что ось вращения ${displaystyle A}$ также является собственным вектором ${displaystyle B}$ соответствующий собственному значению -1.

Плоскость вращения

Поскольку каждое трехмерное вращение имеет ось вращения, также каждое трехмерное вращение имеет плоскость, которая перпендикулярна оси вращения, и которая остается неизменной при вращении. Вращение, ограниченное этой плоскостью, является обычным двумерным вращением.

Доказательство проводится аналогично предыдущему обсуждению. Во-первых, предположим, что все собственные значения трехмерной матрицы вращения A действительны. Это означает, что существует ортогональный базис, состоящий из соответствующих собственных векторов (которые обязательно ортогональны), на который эффект матрицы вращения просто растягивает его. Если в этом базисе писать A, то он диагональный; но диагональная ортогональная матрица состоит только из + 1 и -1 в диагональных элементах. Следовательно, у нас есть не собственное вращение, а либо тождество, либо результат последовательности отражений.

Отсюда следует, что собственное вращение имеет комплексное собственное значение. Пусть v - соответствующий собственный вектор. Затем, как мы показали в предыдущем разделе, ${displaystyle {ar {v}}}$ также является собственным вектором, и ${displaystyle v + {ar {v}}}$ и ${displaystyle i (v- {ar {v}})}$ таковы, что их скалярное произведение обращается в нуль:

{displaystyle i (v ^ {T} + {ar {v}} ^ {T}) (v- {ar {v}}) = i (v ^ {T} v- {ar {v}} ^ {T } {ar {v}} + {ar {v}} ^ {T} vv ^ {T} {ar {v}}) = 0}

потому что, поскольку ${displaystyle {ar {v}} ^ {T} {ar {v}}}$ реально, он равен комплексно сопряженному ${displaystyle v ^ {T} v}$ , и ${displaystyle {ar {v}} ^ {T} v}$ и ${displaystyle v ^ {T} {ar {v}}}$ оба представления одного и того же скалярного произведения между ${displaystyle v}$ и ${displaystyle {ar {v}}}$ .

Это означает ${displaystyle v + {ar {v}}}$ и ${displaystyle i (v- {ar {v}})}$ ортогональные векторы. Кроме того, они оба являются действительными векторами по построению. Эти векторы охватывают то же подпространство, что и ${displaystyle v}$ и ${displaystyle {ar {v}}}$ , которое является инвариантным подпространством относительно приложения A. Следовательно, они покрывают инвариантную плоскость.

Эта плоскость ортогональна инвариантной оси, которая соответствует оставшемуся собственному вектору A с собственным значением 1 из-за ортогональности собственных векторов A.

Смотрите также

Абсолютное вращение - вращение не зависит от каких-либо внешних ссылок
Балансировочная машина
Круговое движение - Движение объекта по круговой траектории
Принцип маха - Понятие абсолютного вращения
Нанодантант, самый быстрый объект вращения
Ориентация (геометрия) - Понятие указания направления
Прокатка
Вращение вокруг фиксированной оси - Тип движения
Формализмы вращения в трех измерениях - способы представления трехмерных вращений
Вращающееся движение в живых системах - движение живых организмов посредством вращения всего тела или части тела
Вершина
Надстройка грузовика

внешняя ссылка

«Вращение», Энциклопедия математики, EMS Press, 2001 [1994]
Продукт вращений в завязать узел. cut-the-knot.org
Когда треугольник равносторонний в узлом. cut-the-knot.org
Поворот точек с использованием полярных координат, howtoproperly.com
Вращение в двух измерениях Серхио Ганнибал Мехиа после работы Роджера Гермундссона и Что такое 3D-вращение Роджер Гермундссон, Вольфрам Демонстрационный проект. демонстрации.wolfram.com
Вращение, отражение и смена кадра: ортогональные тензоры в вычислительной инженерной механике, IOP Publishing

[1] "Оазис или тайное логово?". Изображение недели ESO. В архиве из оригинала 11 октября 2013 г.. Получено 8 октября 2013.

[2] Браннон Р.М., «Поворот, отражение и смена кадра», 2018

[1]

[2]