Кватернион - Quaternion

Эта статья о кватернионах в математике. Для использования в других целях см. Кватернион (значения).

Кватернионное умножение

↓ × →	1	я	j	k
1	1	я	j	k
я	я	−1	k	−j
j	j	−k	−1	я
k	k	j	−я	−1

График Кэли Q8, показывающий циклы умножения на я, j и k – в файл SVG, наведите указатель мыши на цикл или щелкните его, чтобы выделить его

В математика, то кватернионы площадь система счисления что расширяет сложные числа. Впервые их описал ирландский математик. Уильям Роуэн Гамильтон в 1843 г.^[1][2] и применяется к механика в трехмерное пространство. Особенностью кватернионов является то, что умножение двух кватернионов есть некоммутативный. Гамильтон определил кватернион как частное двух направленных линий в трехмерном пространстве^[3] или эквивалентно как частное двух векторов.^[4]

Кватернионы обычно представлены в виде:

${\displaystyle a+b\ \mathbf {i} +c\ \mathbf {j} +d\ \mathbf {k} }$

где а, б, c, и d настоящие числа, и я, j, и k являются фундаментальными кватернионные единицы.

Кватернионы используются в чистая математика, а также имеют практическое применение в Прикладная математика - в частности для расчеты с использованием трехмерных вращений например, в трехмерная компьютерная графика, компьютерное зрение, и кристаллографическая текстура анализ.^[5] В практических приложениях их можно использовать вместе с другими методами, такими как Углы Эйлера и матрицы вращения, или как альтернатива им, в зависимости от приложения.

На современном математическом языке кватернионы образуют четырехугольник.размерный ассоциативный нормированная алгебра с делением над действительные числа, а значит, и домен. Фактически кватернионы были первыми некоммутативная алгебра с делением быть обнаруженным. Алгебру кватернионов часто обозначают как ЧАС (для Гамильтон) или в классная доска жирным шрифтом от ${\displaystyle \mathbb {H} }$ (Unicode U + 210D, ℍ). Это также может быть Алгебра Клиффорда классификации Cl_0,2(ℝ) ≅ Cl⁺
_3,0(ℝ). Алгебра ℍ занимает особое место в анализе, поскольку, согласно Теорема Фробениуса, это одна из двух конечномерных делительные кольца содержащий действительные числа как должное подкольцо, а другой - комплексные числа. Эти кольца тоже Евклидовы алгебры Гурвица, из которых кватернионы самые большие ассоциативная алгебра. Дальнейшее расширение кватернионов дает неассоциативный октонионы, который является последним нормированная алгебра с делением над реалами (расширение октонионов, седенионы, имеет делители нуля и поэтому не может быть нормированной алгеброй с делением).^[6]

В кватернионы единиц можно рассматривать как выбор структуры группы на 3-сфера S³ что дает группе Отжим (3), который изоморфен SU (2) а также к универсальный чехол из ТАК (3).

Графическое представление произведений кватернионных единиц в виде поворотов на 90 ° в плоскостях 4D-пространства, охваченных двумя из {1, я, j, k}. Левый коэффициент можно принять как повернутый вправо. Например:
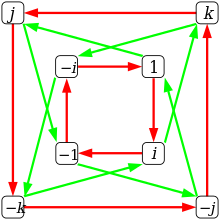
синим цветом: 1 /я-плоскость: 1 ⋅я = я, я/k-самолет: я ⋅ j = k
в красный: 1/j-плоскость: 1 ⋅j = j, j/k-самолет: j ⋅ я = -k

История

Основная статья: История кватернионов

Кватернионная табличка на Мост Брум (Метла), Дублин, в котором говорится:

Здесь, когда он проходил мимо
16 октября 1843 г.
Сэр Уильям Роуэн Гамильтон
во вспышке гения обнаружил
основная формула для
умножение кватернионов
я² = j² = k² = я j k = −1
И вырезать его на камне этого моста

Кватернионы были введены Гамильтоном в 1843 году.^[7] Важными предшественниками этой работы были Тождество Эйлера с четырьмя квадратами (1748) и Олинде Родригес ' параметризация общих вращений по четырем параметрам (1840), но ни один из этих авторов не рассматривал четырехпараметрические вращения как алгебру.^[8][9] Карл Фридрих Гаусс также открыл кватернионы в 1819 году, но эта работа не была опубликована до 1900 года.^[10][11]

Гамильтон знал, что сложные числа можно интерпретировать как точки в самолет, и он искал способ сделать то же самое для точек в трехмерном Космос. Точки в пространстве могут быть представлены их координатами, которые представляют собой тройки чисел, и в течение многих лет он умел складывать и вычитать тройки чисел. Однако Гамильтон долгое время был зациклен на проблеме умножения и деления. Он не мог понять, как рассчитать частное координат двух точек в пространстве. По факту, Фердинанд Георг Фробениус позже доказано в 1877 г. алгебра с делением над действительными числами, чтобы быть конечномерными и ассоциативными, он не может быть трехмерным, и есть только три таких алгебры с делением: ℝ, ℂ (комплексное число) и ℍ (кватернион), которые имеют 1, 2 и 4 измерения соответственно .

Великий прорыв в кватернионах, наконец, произошел в понедельник 16 октября 1843 г. Дублин, когда Гамильтон был на пути к Королевская ирландская академия где он собирался председательствовать на заседании совета. Когда он шел по тропинке Королевский канал вместе с женой концепции кватернионов обретали форму в его сознании. Когда до него дошел ответ, Гамильтон не смог устоять перед желанием высечь формулу для кватернионов:

${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i\,j\,k} =-1}$

в камень Мост Брумэ как он остановился на нем. Хотя резьба с тех пор исчезла, с 1989 года ежегодно проводится паломничество под названием Hamilton Walk для ученых и математиков, которые Дансинкская обсерватория к мосту через Королевский канал в память об открытии Гамильтона.

На следующий день Гамильтон написал письмо своему другу и коллеге-математику Джону Т. Грейвсу, в котором описал ход мыслей, который привел к его открытию. Это письмо позже было опубликовано в письме к Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал;^[12] Гамильтон заявляет:

И здесь меня осенило, что мы должны в некотором смысле допустить четвертое измерение пространства для целей вычисления с тройками ... Электрическая цепь, казалось, замкнулась, и вспыхнула искра.^[12]

Гамильтон назвал четверку с этими правилами умножения кватернион, и он посвятил большую часть своей жизни их изучению и обучению. Лечение Гамильтона более геометрический чем современный подход, который подчеркивает кватернионы ' алгебраический свойства. Он основал школу «кватернионистов» и попытался популяризировать кватернионы в нескольких книгах. Последняя и самая длинная из его книг, Элементы кватернионов,^[13] был 800 страниц; это было отредактировано его сын и опубликован вскоре после его смерти.

После смерти Гамильтона его ученица Питер Тейт продолжил продвижение кватернионов. В то время кватернионы были обязательной темой экзаменов в Дублине. Темы физики и геометрии, которые теперь можно было бы описывать с помощью векторов, например кинематика в космосе и Уравнения Максвелла, были полностью описаны в терминах кватернионов. Была даже профессиональная исследовательская ассоциация, Общество Кватерниона, посвященный изучению кватернионов и других гиперкомплексное число системы.

С середины 1880-х гг. Кватернионы стали вытесняться векторный анализ, который был разработан Джозайя Уиллард Гиббс, Оливер Хевисайд, и Герман фон Гельмгольц. Векторный анализ описывал те же явления, что и кватернионы, поэтому некоторые идеи и терминологию были заимствованы из литературы по кватернионам. Однако векторный анализ был концептуально проще и чище с нотации, и в конечном итоге кватернионам отводилась второстепенная роль в математика и физика. Побочным эффектом этого перехода является то, что Работа Гамильтона сложно понять многим современным читателям. Первоначальные определения Гамильтона незнакомы, а его стиль письма многословен и труден для понимания.

Однако кватернионы возродились с конца 20 века, в первую очередь из-за их полезности в описание пространственных вращений. Представления поворотов кватернионами более компактны и вычисляются быстрее, чем представления матрицами. Кроме того, в отличие от Углы Эйлера, они не восприимчивы к "карданный замок ». По этой причине кватернионы используются в компьютерная графика,^[14][15] компьютерное зрение, робототехника,^[16] теория управления, обработка сигнала, контроль отношения, физика, биоинформатика,^[17][18] молекулярная динамика, компьютерное моделирование, и орбитальная механика. Например, это обычное явление для контроль отношения системы космических аппаратов, которыми нужно управлять в терминах кватернионов. Кватернионы получили дополнительный импульс от теория чисел из-за их отношений с квадратичные формы.^[19]

Кватернионы в физике

Очерк П.Р. Жирара 1984 года Группа кватернионов и современная физика^[20] обсуждает некоторые роли кватернионов в физике. В эссе показано, как различные группы физической ковариации, а именно ТАК (3), группа Лоренца, группа общей теории относительности, алгебра Клиффорда SU (2) и конформную группу, легко связать с группа кватернионов в современная алгебра. Жирар начал с обсуждения групповые представления и представляя некоторые космические группы из кристаллография. Он приступил к кинематика из жесткое тело движение. Затем он использовал сложные кватернионы (бикватернионы ) для представления Группа Лоренца специальной теории относительности, в том числе Прецессия Томаса. Он процитировал пять авторов, начиная с Людвик Зильберштейн, кто использовал потенциал функция одного кватернионная переменная выражать Уравнения Максвелла в единственном дифференциальное уравнение. Что касается общей теории относительности, он выразил Вектор Рунге – Ленца. Он упомянул бикватернионы Клиффорда (сплит-бикватернионы ) как экземпляр Алгебра Клиффорда. Наконец, используя аналог бикватерниона, Жирар описал конформные карты на пространство-время. Среди пятидесяти упоминаний Жирар включил Александр Макфарлейн и его Бюллетень из Общество Кватерниона. В 1999 году он показал, как уравнения общей теории относительности Эйнштейна могут быть сформулированы в рамках алгебры Клиффорда, которая напрямую связана с кватернионами.^[21]

Открытие 1924 г., что в квантовая механика то вращение электрона и других частиц материи (известных как спиноры ) могут быть описаны с помощью кватернионов, способствующих их интересу; кватернионы помогли понять, как вращения электронов на 360 ° можно отличить от вращений на 720 ° («Трюк с тарелкой ”).^[22][23] По состоянию на 2018 год^{[Обновить]}, их использование не настигло группы ротации.^[а]

Определение

А кватернион является выражение формы

${\displaystyle a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} \ ,}$

где а, б, c, d, находятся действительные числа, и я, j, k, находятся символы это можно интерпретировать как единичные векторы, указывающие вдоль трех пространственных осей. На практике, если один из а, б, c, d равно 0, соответствующий член опущен; если а, б, c, d все равны нулю, кватернион - это нулевой кватернион, обозначается 0; если один из б, c, d равно 1, соответствующий член записывается просто я, j, или k.

Гамильтон описывает кватернион ${\displaystyle q=a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$, как состоящий из скаляр часть и векторная часть. Кватернион ${\displaystyle b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$ называется векторная часть (иногда мнимая часть) из q, и а это скалярная часть (иногда реальная часть) из q. Кватернион, равный его действительной части (то есть его векторная часть равна нулю), называется скаляр или настоящий кватернион, и обозначается соответствующим действительным числом. То есть настоящие числа встроенный в кватернионах. (Более точно, поле действительных чисел изоморфно подмножеству кватернионов. Поле комплексных чисел также изоморфно трем подмножествам кватернионов.)^[24] Кватернион, равный своей векторной части, называется вектор кватернион.

Набор кватернионов выполнен в виде 4-х мерного векторное пространство над реальными числами, с ${\displaystyle \left\{\,1,\mathbf {i} ,\mathbf {j} ,\mathbf {k} \,\right\}}$ как основа, покомпонентным сложением

${\displaystyle (a_{1}+b_{1}\,\mathbf {i} +c_{1}\,\mathbf {j} +d_{1}\,\mathbf {k} )+(a_{2}+b_{2}\,\mathbf {i} +c_{2}\,\mathbf {j} +d_{2}\,\mathbf {k} )=(a_{1}+a_{2})+(b_{1}+b_{2})\,\mathbf {i} +(c_{1}+c_{2})\,\mathbf {j} +(d_{1}+d_{2})\,\mathbf {k} \,,}$

и покомпонентное скалярное умножение

${\displaystyle \lambda (a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )=\lambda a+(\lambda b)\,\mathbf {i} +(\lambda c)\,\mathbf {j} +(\lambda d)\,\mathbf {k} .}$

Мультипликативная групповая структура, называемая Гамильтон продукт, обозначаемые сопоставлением, могут быть определены на кватернионах следующим образом:

• Настоящий кватернион 1 это элемент идентичности.
• В настоящий кватернионы коммутируют со всеми другими кватернионами, то есть водный = qa для каждого кватерниона q и каждый настоящий кватернион а. В алгебраической терминологии это означает, что поле действительных кватернионов является центр этой кватернионной алгебры.
• Произведение сначала дается для базовых элементов (см. Следующий подраздел), а затем распространяется на все кватернионы с помощью распределительное свойство и центральное свойство реальных кватернионов. Продукт Гамильтона не коммутативный, но это ассоциативный, таким образом, кватернионы образуют ассоциативная алгебра над реалами.
• Кроме того, каждый ненулевой кватернион имеет обратный по отношению к произведению Гамильтона:

${\displaystyle (a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} )^{-1}={\frac {1}{a^{2}+b^{2}+c^{2}+d^{2}}}\,(a-b\,\mathbf {i} -c\,\mathbf {j} -d\,\mathbf {k} ).}$

Таким образом, кватернионы образуют алгебра с делением.

Умножение базисных элементов

Таблица умножения

Некоммутативность подчеркнута цветными квадратами.

×	1	я	j	k
1	1	я	j	k
я	я	−1	k	−j
j	j	−k	−1	я
k	k	j	−я	−1

Базовые элементы я, j, и k коммутируют с реальным кватернионом 1, то есть

${\displaystyle \mathbf {i} \cdot 1=1\cdot \mathbf {i} =\mathbf {i} ,\qquad \mathbf {j} \cdot 1=1\cdot \mathbf {j} =\mathbf {j} ,\qquad \mathbf {k} \cdot 1=1\cdot \mathbf {k} =\mathbf {k} \,.}$

Остальные произведения базовых элементов определяются как

${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=-1\,,}$

и

${\displaystyle {\begin{alignedat}{2}\mathbf {ij} &=\mathbf {k} \,,&\qquad \mathbf {ji} &=-\mathbf {k} \,,\\\mathbf {jk} &=\mathbf {i} \,,&\mathbf {kj} &=-\mathbf {i} \,,\\\mathbf {ki} &=\mathbf {j} \,,&\mathbf {ik} &=-\mathbf {j} \,.\end{alignedat}}}$

Эти формулы умножения эквивалентны

${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {ijk} =-1~.}$

Фактически равенство ijk = –1 результаты из

${\displaystyle (\mathbf {ij} )\mathbf {k} =\mathbf {k} ^{2}=-1.}$

Обратное утверждение является результатом манипуляций, подобных следующим. Умножая обе части −1 = ijk от –k, получается

${\displaystyle \mathbf {k} =(\mathbf {ijk} )(-\mathbf {k} )=(\mathbf {ij} )(-\mathbf {k} ^{2})=\mathbf {ij} \,.}$

Все остальные продукты можно определить аналогичными методами.

Центр

В центр из некоммутативное кольцо это подкольцо элементов c такой, что сх = xc для каждого Икс. Центр алгебры кватернионов - это подполе вещественных кватернионов. Фактически, это часть определения, что настоящие кватернионы принадлежат центру. Наоборот, если q = а + б я + c j + d k принадлежит центру, то

${\displaystyle 0=\mathbf {i} \,q-q\,\mathbf {i} =2c\,\mathbf {ij} +2d\,\mathbf {ik} =2c\,\mathbf {k} -2d\,\mathbf {j} \,,}$

и c = d = 0. Аналогичное вычисление с j вместо того я показывает, что есть также б = 0. Таким образом q = а это настоящий кватернион.

Кватернионы образуют алгебра с делением. Это означает, что некоммутативность умножения - единственное свойство, которое отличает кватернионы от поле. Эта некоммутативность имеет несколько неожиданных последствий, среди которых полиномиальное уравнение над кватернионами может иметь больше различных решений, чем степень полинома. Например, уравнение z² + 1 = 0, имеет бесконечно много решений кватернионов, которые являются кватернионами z = б я + c j + d k такой, что б² + c² + d² = 1. Таким образом, эти «корни из –1» образуют единичная сфера в трехмерном пространстве векторных кватернионов.

Гамильтон продукт

Для двух элементов а₁ + б₁я + c₁j + d₁k и а₂ + б₂я + c₂j + d₂k, их продукт, названный Гамильтон продукт (а₁ + б₁я + c₁j + d₁k) (а₂ + б₂я + c₂j + d₂k), определяется произведением базисных элементов и распределительный закон. Закон распределения позволяет расширить продукт так, чтобы он представлял собой сумму произведений основных элементов. Это дает следующее выражение:

${\displaystyle {\begin{alignedat}{4}&a_{1}a_{2}&&+a_{1}b_{2}\mathbf {i} &&+a_{1}c_{2}\mathbf {j} &&+a_{1}d_{2}\mathbf {k} \\{}+{}&b_{1}a_{2}\mathbf {i} &&+b_{1}b_{2}\mathbf {i} ^{2}&&+b_{1}c_{2}\mathbf {ij} &&+b_{1}d_{2}\mathbf {ik} \\{}+{}&c_{1}a_{2}\mathbf {j} &&+c_{1}b_{2}\mathbf {ji} &&+c_{1}c_{2}\mathbf {j} ^{2}&&+c_{1}d_{2}\mathbf {jk} \\{}+{}&d_{1}a_{2}\mathbf {k} &&+d_{1}b_{2}\mathbf {ki} &&+d_{1}c_{2}\mathbf {kj} &&+d_{1}d_{2}\mathbf {k} ^{2}\end{alignedat}}}$

Теперь базовые элементы можно умножить, используя приведенные выше правила, чтобы получить:^[7]

${\displaystyle {\begin{alignedat}{4}&a_{1}a_{2}&&-b_{1}b_{2}&&-c_{1}c_{2}&&-d_{1}d_{2}\\{}+{}(&a_{1}b_{2}&&+b_{1}a_{2}&&+c_{1}d_{2}&&-d_{1}c_{2})\mathbf {i} \\{}+{}(&a_{1}c_{2}&&-b_{1}d_{2}&&+c_{1}a_{2}&&+d_{1}b_{2})\mathbf {j} \\{}+{}(&a_{1}d_{2}&&+b_{1}c_{2}&&-c_{1}b_{2}&&+d_{1}a_{2})\mathbf {k} \end{alignedat}}}$

Произведение двух кватернионы вращения^[25] будет эквивалентно вращению а₂ + б₂я + c₂j + d₂k с последующим вращением а₁ + б₁я + c₁j + d₁k.

Скалярная и векторная части

Кватернион формы а + 0 я + 0 j + 0 k, где а это действительное число, называется скаляр, и кватернион вида 0 + б я + c j + d k, где б, c, и d являются действительными числами, и хотя бы одно из б, c или d отличен от нуля, называется вектор кватернион. Если а + б я + c j + d k любой кватернион, то а называется его скалярная часть и б я + c j + d k называется его векторная часть. Несмотря на то, что каждый кватернион можно рассматривать как вектор в четырехмерном векторном пространстве, принято ссылаться на вектор часть как векторы в трехмерном пространстве. Согласно этому соглашению вектор - это то же самое, что и элемент векторного пространства. ℝ³.^[b]

Гамильтон также называл векторными кватернионами правые кватернионы^[27][28] и действительные числа (рассматриваются как кватернионы с нулевой частью вектора) скалярные кватернионы.

Если кватернион разделен на скалярную часть и векторную часть, т.е.

${\displaystyle \mathbf {q} =(r,\ {\vec {v}}),~~\mathbf {q} \in \mathbb {H} ,~~r\in \mathbb {R} ,~~{\vec {v}}\in \mathbb {R} ^{3}}$

тогда формулы для сложения и умножения следующие:

${\displaystyle (r_{1},\ {\vec {v}}_{1})+(r_{2},\ {\vec {v}}_{2})=(r_{1}+r_{2},\ {\vec {v}}_{1}+{\vec {v}}_{2})}$

${\displaystyle (r_{1},\ {\vec {v}}_{1})(r_{2},\ {\vec {v}}_{2})=(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_{2}+r_{2}{\vec {v}}_{1}+{\vec {v}}_{1}\times {\vec {v}}_{2})}$

где "·" это скалярное произведение и "×" это перекрестное произведение.

Спряжение, норма и реципрокность

Сопряжение кватернионов аналогично сопряжению комплексных чисел и транспонированию (также известному как обращение) элементов Алгебры Клиффорда. Чтобы определить это, пусть ${\displaystyle q=a+b\,\mathbf {i} +c\,\mathbf {j} +d\,\mathbf {k} }$ быть кватернионом. В сопрягать из q это кватернион ${\displaystyle q^{*}=a-b\,\mathbf {i} -c\,\mathbf {j} -d\,\mathbf {k} }$. Обозначается он q^∗, q^т, ${\displaystyle {\tilde {q}}}$, или q.^[7] Спряжение - это инволюция, что означает, что это собственный обратный элемент, поэтому двойное сопряжение элемента возвращает исходный элемент. Конъюгат продукта двух кватернионов является продуктом конъюгатов в обратном порядке. То есть, если п и q кватернионы, то (pq)^∗ = q^∗п^∗не п^∗q^∗.

Сопряжение кватерниона, в отличие от сложной настройки, может быть выражено умножением и сложением кватернионов:

${\displaystyle q^{*}=-{\frac {1}{2}}(q+\,\mathbf {i} \,q\,\mathbf {i} +\,\mathbf {j} \,q\,\mathbf {j} +\,\mathbf {k} \,q\,\mathbf {k} )~.}$

Сопряжение можно использовать для извлечения скалярной и векторной частей кватерниона. Скалярная часть п является 1/2(п + п^∗) , и векторная часть п является 1/2(п − п^∗) .

Квадратный корень из произведения кватерниона на сопряженный ему элемент называется его норма и обозначается ||q|| (Гамильтон назвал эту величину тензор из q, но это противоречит современному значению слова "тензор "). В формуле это выражается следующим образом:

${\displaystyle \lVert q\rVert ={\sqrt {\,qq^{*}~}}={\sqrt {\,q^{*}q~}}={\sqrt {\,a^{2}+b^{2}+c^{2}+d^{2}~}}}$

Это всегда неотрицательное действительное число, и оно совпадает с евклидовой нормой на ℍ рассматривается как векторное пространство ℝ⁴. При умножении кватерниона на действительное число его норма масштабируется на абсолютное значение числа. То есть, если α реально, тогда

${\displaystyle \lVert \alpha q\rVert =\left|\alpha \right|\,\lVert q\rVert ~.}$

Это частный случай того, что норма мультипликативный, означающий, что

${\displaystyle \lVert pq\rVert =\lVert p\rVert \,\lVert q\rVert }$

для любых двух кватернионов п и q. Мультипликативность - это следствие формулы для сопряженного произведения. В качестве альтернативы она следует из тождества.

${\displaystyle \det {\Bigl (}{\begin{array}{cc}a+ib&id+c\\id-c&a-ib\end{array}}{\Bigr )}=a^{2}+b^{2}+c^{2}+d^{2},}$

(где я обозначает обычный мнимая единица ) и, следовательно, из мультипликативного свойства детерминанты квадратных матриц.

Эта норма позволяет определить расстояние d(п, q) между п и q как норма их разницы:

${\displaystyle d(p,q)=\lVert p-q\rVert ~.}$

Это делает ℍ а метрическое пространство. Сложение и умножение непрерывны в метрической топологии. Действительно, для любого скаляра положительное а он держит

${\displaystyle \lVert (p+ap_{1}+q+aq_{1})-(p+q)\rVert =a\lVert p_{1}+q_{1}\rVert \,.}$

Непрерывность следует из взятия а до нуля в пределе. Аналогичным образом выполняется непрерывность умножения.

Кватернион единицы

Основная статья: Versor

А кватернион единиц является кватернионом единицы нормы. Деление ненулевого кватерниона q по своей норме производит единичный кватернион Uq называется Versor из q:

${\displaystyle \mathbf {U} q={\frac {q}{\lVert q\rVert }}.}$

Каждый кватернион имеет полярное разложение ${\displaystyle q=\lVert q\rVert \cdot \mathbf {U} q}$.

Использование сопряжения и нормы позволяет определить взаимный ненулевого кватерниона. Произведение кватерниона на обратное должно равняться 1, и приведенные выше соображения подразумевают, что произведение ${\displaystyle q}$ и ${\displaystyle q^{*}/\left\Vert q\right\|^{2}}$ равно 1 (для любого порядка умножения). Так что взаимный из q определяется как

${\displaystyle q^{-1}={\frac {q^{*}}{\lVert q\rVert ^{2}}}.}$

Это позволяет разделить два кватерниона п и q двумя разными способами (когда q не равно нулю). То есть их частное может быть либо p q⁻¹ или q⁻¹п ; как правило, эти произведения различаются в зависимости от порядка умножения, за исключением особого случая, когда п и q являются скалярными, кратными друг другу (включая случай, когда п = 0). Следовательно, обозначение п/q неоднозначно, поскольку не указывает, q делится слева или справа (независимо от того, q⁻¹ умножается п слева или справа).

Алгебраические свойства

Граф Кэли из Q₈. Красные стрелки представляют умножение справа на я, а зеленые стрелки представляют умножение справа на j.

Набор ℍ всех кватернионов векторное пространство над действительные числа с участием измерение  4.^[c] Умножение кватернионов ассоциативно и распределяется по сложению векторов, но, за исключением скалярного подмножества, оно не коммутативно. Следовательно, кватернионы ℍ некоммутативны, ассоциативная алгебра над реальными числами. Даже не смотря на ℍ содержит копии комплексных чисел, это не ассоциативная алгебра над комплексными числами.

Поскольку кватернионы можно разделить, они образуют алгебра с делением. Это структура, похожая на поле за исключением некоммутативности умножения. Конечномерные ассоциативные алгебры с делением над действительными числами очень редки. В Теорема Фробениуса заявляет, что их ровно три: ℝ, ℂ, и ℍ. Норма превращает кватернионы в нормированная алгебра, и нормированные алгебры с делением над действительными также очень редки: Теорема Гурвица говорит, что их всего четыре: ℝ, ℂ, ℍ, и ${\displaystyle \mathbb {O} }$ (в октонионы ). Кватернионы также являются примером композиционная алгебра и единого Банахова алгебра.

Трехмерный график Q₈. Красные, зеленые и синие стрелки обозначают умножение на я, j, и kсоответственно. Умножение на отрицательные числа для ясности опущено.

Поскольку произведение любых двух базисных векторов равно плюс или минус другому базисному вектору, набор {±1, ±я, ±j, ±k} образует группа при умножении. Этот не-абелева группа называется группа кватернионов и обозначается Q₈.^[29] Реальность групповое кольцо из Q₈ кольцо ℝ [Q₈] которое также является восьмимерным векторным пространством над ℝ. Он имеет один базисный вектор для каждого элемента Q₈. Кватернионы изоморфны кольцо частного из ℝ [Q₈] посредством идеальный порожденный элементами 1 + (−1), я + (−я) , j + (−j), и k + (−k). Здесь первый член в каждом из различий является одним из основных элементов. 1, я, j, и k, а второй член - один из базисных элементов −1, −я, −j, и −k, а не аддитивные инверсии 1, я, j, и k.

Кватернионы и геометрия ℝ³

Векторная часть кватерниона может быть интерпретирована как вектор координат в ℝ³; следовательно, алгебраические операции кватернионов отражают геометрию ℝ³. Такие операции, как векторные точки и перекрестные произведения, могут быть определены в терминах кватернионов, и это позволяет применять методы кватернионов везде, где возникают пространственные векторы. Полезное применение кватернионов - интерполировать ориентацию ключевых кадров в компьютерной графике.^[14]

В оставшейся части этого раздела я, j, и k будет обозначать как три воображаемых^[30] базисные векторы ℍ и основа для ℝ³. Замена я от −я, j от −j, и k от −k отправляет вектор своему аддитивному инверсному, поэтому аддитивный инверсный вектор совпадает с его сопряженным в качестве кватерниона. По этой причине спряжение иногда называют пространственная инверсия.

Для двух векторных кватернионов п = б₁я + c₁j + d₁k и q = б₂я + c₂j + d₂k их скалярное произведение, по аналогии с векторами в ℝ³, является

${\displaystyle p\cdot q=b_{1}b_{2}+c_{1}c_{2}+d_{1}d_{2}~.}$

Это также может быть выражено без компонентов как

${\displaystyle p\cdot q=\textstyle {\frac {1}{2}}(p^{*}q+q^{*}p)=\textstyle {\frac {1}{2}}(pq^{*}+qp^{*}).}$

Это равно скалярным частям произведений pq^∗, qp^∗, п^∗q, и q^∗п. Обратите внимание, что их векторные части разные.

В перекрестное произведение из п и q относительно ориентации, определяемой упорядоченным базисом я, j, и k является

${\displaystyle p\times q=(c_{1}d_{2}-d_{1}c_{2})\mathbf {i} +(d_{1}b_{2}-b_{1}d_{2})\mathbf {j} +(b_{1}c_{2}-c_{1}b_{2})\mathbf {k} \,.}$

(Напомним, что ориентация необходима для определения знака.) Это равно векторной части произведения. pq (как кватернионы), а также векторная часть −q^∗п^∗. Он также имеет формулу

${\displaystyle p\times q=\textstyle {\tfrac {1}{2}}(pq-qp).}$

Для коммутатор, [п, q] = pq − qp, из двух векторных кватернионов получается

${\displaystyle [p,q]=2p\times q.}$

В общем, пусть п и q быть кватернионами и написать

${\displaystyle p=p_{\text{s}}+p_{\text{v}},}$

${\displaystyle q=q_{\text{s}}+q_{\text{v}},}$

где п_s и q_s - скалярные части, а п_v и q_v векторные части п и q. Тогда у нас есть формула

${\displaystyle pq=(pq)_{\text{s}}+(pq)_{\text{v}}=(p_{\text{s}}q_{\text{s}}-p_{\text{v}}\cdot q_{\text{v}})+(p_{\text{s}}q_{\text{v}}+q_{\text{s}}p_{\text{v}}+p_{\text{v}}\times q_{\text{v}}).}$

Это показывает, что некоммутативность умножения кватернионов происходит от умножения векторных кватернионов. Это также показывает, что два кватерниона коммутируют тогда и только тогда, когда их векторные части коллинеарны. Гамильтон^[31] показал, что это произведение вычисляет третью вершину сферического треугольника из двух заданных вершин и связанных с ними длин дуги, которая также является алгеброй точек в Эллиптическая геометрия.

Кватернионы единиц могут быть идентифицированы вращением в ℝ³ и были названы версоры пользователя Hamilton.^[31] Также см Кватернионы и пространственное вращение для получения дополнительной информации о моделировании трехмерного вращения с помощью кватернионов.

Увидеть Hanson (2005)^[32] для визуализации кватернионов.

Матричные представления

Так же, как комплексные числа могут быть представлены в виде матриц и кватернионы тоже. Есть как минимум два способа представления кватернионов в виде матрицы таким образом, что сложение кватернионов и умножение соответствуют сложению матриц и матричное умножение. Один - использовать 2 × 2 сложный матрицы, а другой - использовать 4 × 4 настоящий матрицы. В каждом случае данное представление является одним из семейства линейно связанных представлений. В терминологии абстрактная алгебра, Эти инъективный гомоморфизмы от ℍ к матричные кольца М (2, ℂ) и М (4, ℝ), соответственно.

Используя комплексные матрицы 2 × 2, кватернион а + би + cj + dk можно представить как

${\displaystyle {\begin{bmatrix}a+bi&c+di\\-c+di&a-bi\end{bmatrix}}.}$

Это представление обладает следующими свойствами:

• Ограничение любых двух из б, c и d к нулю дает представление сложные числа. Например, установка c = d = 0 производит диагональное комплексное матричное представление комплексных чисел и устанавливает б = d = 0 производит реальное матричное представление.
• Норма кватерниона (квадратный корень из произведения с его сопряженным, как с комплексными числами) - это квадратный корень из детерминант соответствующей матрицы.^[33]
• Сопряжение кватерниона соответствует сопряженный транспонировать матрицы.
• По ограничению это представление дает изоморфизм между подгруппой единичных кватернионов и их изображением SU (2). Топологически кватернионы единиц являются 3-сфера, поэтому основное пространство SU (2) также является 3-сферой. Группа SU (2) важно для описания вращение в квантовая механика; увидеть Матрицы Паули.
• Между кватернионными единицами и матрицами Паули существует сильная связь. Получите восемь единичных матриц кватернионов, взяв а, б, c и dустановите три из них на ноль, а четвертый на 1 или −1. Умножение любых двух матриц Паули всегда дает единичную матрицу кватернионов, все они кроме −1. Через я² = j² = k² = я j k = −1; например последнее равенство

${\displaystyle {\begin{aligned}ijk=\sigma _{1}\sigma _{2}\sigma _{3}\sigma _{1}\sigma _{2}\sigma _{3}=-1\end{aligned}}}$

Используя вещественные матрицы 4 × 4, тот же кватернион можно записать как

${\displaystyle {\begin{bmatrix}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{bmatrix}}=a{\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}+b{\begin{bmatrix}0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix}}+c{\begin{bmatrix}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{bmatrix}}+d{\begin{bmatrix}0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{bmatrix}}.}$

Однако представление кватернионов в М (4, ℝ) не уникален. Например, тот же кватернион также может быть представлен как

${\displaystyle {\begin{bmatrix}a&d&-b&-c\\-d&a&c&-b\\b&-c&a&-d\\c&b&d&a\end{bmatrix}}=a{\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}+b{\begin{bmatrix}0&0&-1&0\\0&0&0&-1\\1&0&0&0\\0&1&0&0\end{bmatrix}}+c{\begin{bmatrix}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{bmatrix}}+d{\begin{bmatrix}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix}}.}$

Существует 48 различных матричных представлений этой формы, в которых одна из матриц представляет скалярную часть, а остальные три являются кососимметричными. Точнее, существует 48 наборов четверок матриц с этими ограничениями симметрии, так что функция, отправляющая 1, я, j, и k к матрицам в четверке является гомоморфизмом, то есть переводит суммы и произведения кватернионов в суммы и произведения матриц.^[34] В этом представлении конъюгат кватерниона соответствует транспонировать матрицы. Четвертая степень нормы кватерниона - это детерминант соответствующей матрицы. Как и в случае комплексного представления 2 × 2, приведенного выше, комплексные числа снова могут быть получены путем соответствующего ограничения коэффициентов; например, в виде блочно-диагональных матриц с двумя блоками 2 × 2, задав c = d = 0.

Каждое матричное представление кватернионов 4 × 4 соответствует таблице умножения единичных кватернионов. Например, последнее приведенное выше матричное представление соответствует таблице умножения

×	а	d	−б	−c
а	а	d	−b	−c
−d	−d	а	c	−b
б	б	−c	а	−d
c	c	б	d	а

который изоморфен - через ${\displaystyle \{a\mapsto 1,b\mapsto i,c\mapsto j,d\mapsto k\}}$ - чтобы

×	1	k	−я	−j
1	1	k	−я	−j
−k	−k	1	j	−я
я	я	−j	1	−k
j	j	я	k	1

Если ограничить любую такую ​​таблицу умножения идентичностью в первой строке и столбце и чтобы знаки заголовков строк были противоположны знакам заголовков столбцов, тогда есть 3 возможных варианта для второго столбца (без учета знака), 2 возможных варианты выбора для третьего столбца (знак игнорирования) и 1 возможный выбор для четвертого столбца (знак игнорирования); что дает 6 возможностей. Затем второй столбец может быть выбран положительным или отрицательным, третий столбец может быть выбран положительным или отрицательным, а четвертый столбец может быть выбран положительным или отрицательным, что дает 8 вариантов для знака. Умножение возможных позиций букв и их знаков дает 48. Затем замена 1 с участием а, я с участием б, j с участием c, и k с участием d и удаление заголовков строк и столбцов дает матричное представление а + б я + c j + d k.

Теорема Лагранжа о четырех квадратах

Основная статья: Теорема Лагранжа о четырех квадратах

Кватернионы также используются в одном из доказательств теоремы Лагранжа о четырех квадратах в теория чисел, который гласит, что каждое неотрицательное целое число является суммой четырех целых квадратов. Теорема Лагранжа о четырех квадратах не только сама по себе элегантная теорема, но и имеет полезные приложения в областях математики за пределами теории чисел, таких как комбинаторный дизайн теория. Доказательство на основе кватернионов использует Кватернионы Гурвица, подкольцо кольца всех кватернионов, для которого существует аналог Евклидов алгоритм.

Кватернионы как пары комплексных чисел

Основная статья: Конструкция Кэли-Диксона

Кватернионы можно представить как пары комплексных чисел. С этой точки зрения кватернионы являются результатом применения Конструкция Кэли-Диксона к комплексным числам. Это обобщение построения комплексных чисел как пар действительных чисел.

Позволять ℂ² - двумерное векторное пространство над комплексными числами. Выбираем основу, состоящую из двух элементов 1 и j. Вектор в ℂ² можно записать в терминах базовых элементов 1 и j так как

${\displaystyle (a+bi)1+(c+di)\mathbf {j} \,.}$

Если мы определим j² = −1 и я j = −j я, тогда мы можем умножить два вектора, используя закон распределения. С помощью k как сокращенное обозначение продукта я j приводит к тем же правилам умножения, что и обычные кватернионы. Следовательно, указанный выше вектор комплексных чисел соответствует кватерниону а + б я + c j + d k. Если мы напишем элементы ℂ² как упорядоченные пары и кватернионы как четверки, то соответствие

${\displaystyle (a+bi,\ c+di)\leftrightarrow (a,b,c,d).}$

Квадратные корни из −1

В комплексных числах ℂ, всего два числа, я и -я, квадрат которого равен −1. В ℍ существует бесконечно много квадратных корней из минус единицы: кватернионное решение для квадратного корня из −1 - это единица сфера в ℝ³. Чтобы увидеть это, позвольте q = а + б я + c j + d k - кватернион, и предположим, что его квадрат равен −1. С точки зрения а, б, c, и d, это означает

${\displaystyle a^{2}-b^{2}-c^{2}-d^{2}=-1,}$

${\displaystyle 2ab=0,}$

${\displaystyle 2ac=0,}$

${\displaystyle 2ad=0.}$

Чтобы удовлетворить последним трем уравнениям, либо а = 0 или б, c, и d все 0. Последнее невозможно, потому что а является действительным числом, и из первого уравнения следует, что а² = −1. Следовательно, а = 0 и б² + c² + d² = 1. Другими словами: кватернион возводится в квадрат до −1 тогда и только тогда, когда он является векторным кватернионом с нормой 1. По определению, множество всех таких векторов образует единичную сферу.

Только отрицательные действительные кватернионы имеют бесконечно много квадратных корней. У всех остальных их всего два (или один в случае 0).^{[нужна цитата ][d]}

ℍ как союз сложных плоскостей

Каждая пара квадратных корней из -1 создает отдельную копию комплексных чисел внутри кватернионов. Если q² = −1, то копия определяется функцией

${\displaystyle a+b{\sqrt {-1\,}}\mapsto a+bq\,.}$

На языке абстрактная алгебра, каждый является инъективный кольцо гомоморфизм от ℂ к ℍ. Образы вложений, соответствующие q и -q идентичны.

Каждый нереальный кватернион определяет плоское подпространство в ℍ что изоморфно ℂ: Написать q как сумму его скалярной части и его векторной части:

${\displaystyle q=q_{s}+{\vec {q}}_{v}.}$

Далее разложите векторную часть как произведение ее нормы и ее Versor:

${\displaystyle q=q_{s}+\lVert {\vec {q}}_{v}\rVert \cdot \mathbf {U} {\vec {q}}_{v}.}$

(Обратите внимание, что это не то же самое, что ${\displaystyle q_{s}+\lVert q\rVert \cdot \mathbf {U} q}$.) Версор векторной части q, ${\displaystyle \mathbf {U} {\vec {q}}_{v}}$, является правым версором с квадратом –1. Следовательно, он определяет копию комплексных чисел функцией

${\displaystyle a+b{\sqrt {-1\,}}\mapsto a+b\mathbf {U} {\vec {q}}_{v}\,.}$

В рамках этой функции q это изображение комплексного числа ${\displaystyle q_{s}+\lVert {\vec {q}}_{v}\rVert i}$. Таким образом ℍ это союз сложных плоскостей, пересекающихся в общем реальная линия, где объединение берется по сфере квадратных корней из минус единицы, имея в виду, что одна и та же плоскость связана с любой парой противоположные точки на сфере правых версоров.

Коммутативные подкольца

Отношения кватернионов друг с другом в сложных подплосках ℍ также могут быть идентифицированы и выражены в терминах коммутативный подколец. В частности, поскольку два кватерниона п и q коммутировать (т. е. p q = q p), только если они лежат в одной и той же сложной подплоскости ℍ, профиль ℍ как объединение сложных плоскостей возникает, когда кто-то пытается найти все коммутативные подкольца кватерниона кольцо. Этот метод коммутативных подколец также используется для профилирования сплит-кватернионы, которые как алгебра над вещественными числами изоморфны 2 × 2 вещественные матрицы.

Функции кватернионной переменной

Основная статья: Кватернионный анализ

Множества Жюлиа и Мандельброта можно расширить до кватернионов, но они должны использовать поперечные сечения для визуализации визуально в 3-х измерениях. Этот набор Джулии разрезан на х у самолет.

Как функции комплексная переменная, функции кватернионной переменной предлагают полезные физические модели. Например, исходные электрические и магнитные поля, описанные Максвеллом, были функциями кватернионной переменной. Примеры других функций включают расширение Набор Мандельброта и Юля наборы в 4-х мерное пространство.^[36]

Экспоненциальные, логарифмические и степенные функции

Учитывая кватернион,

${\displaystyle q=a+b\mathbf {i} +c\mathbf {j} +d\mathbf {k} =a+\mathbf {v} }$

экспонента вычисляется как^[37]

${\displaystyle \exp(q)=\sum _{n=0}^{\infty }{\frac {q^{n}}{n!}}=e^{a}\left(\cos \|\mathbf {v} \|+{\frac {\mathbf {v} }{\|\mathbf {v} \|}}\sin \|\mathbf {v} \|\right)~~}$

и логарифм^[37]

${\displaystyle \ln(q)=\ln \|q\|+{\frac {\mathbf {v} }{\|\mathbf {v} \|}}\arccos {\frac {a}{\|q\|}}~~}$

Отсюда следует, что полярное разложение кватерниона можно записать

${\displaystyle q=\|q\|e^{{\hat {n}}\varphi }=\|q\|\left(\cos(\varphi )+{\hat {n}}\sin(\varphi )\right),}$

где угол ${\displaystyle \varphi }$^[e]

${\displaystyle a=\|q\|\cos(\varphi )}$

и единичный вектор ${\displaystyle {\hat {n}}}$ определяется:

${\displaystyle \mathbf {v} ={\hat {n}}\|\mathbf {v} \|={\hat {n}}\|q\|\sin(\varphi )\,.}$

Любой кватернион единицы может быть выражен в полярной форме как ${\displaystyle e^{{\hat {n}}\varphi }}$.

В мощность кватерниона, возведенного в произвольную (действительную) экспоненту Икс дан кем-то:

${\displaystyle q^{x}=\|q\|^{x}e^{{\hat {n}}x\varphi }=\|q\|^{x}\left(\cos(x\varphi )+{\hat {n}}\,\sin(x\varphi )\right)~.}$

Геодезическая норма

В геодезическое расстояние d_г(п, q) между кватернионами единиц п и q определяется как:

${\displaystyle d_{\text{g}}(p,q)=\lVert \ln(p^{-1}q)\rVert .}$^[39]

и составляет абсолютную величину половины угла, образуемого п и q вдоль большая дуга из S³ Этот угол также можно вычислить из кватерниона скалярное произведение без логарифма как:

${\displaystyle \arccos(2(p\cdot q)^{2}-1).}$

Трехмерные и четырехмерные группы вращения

Основные статьи: Кватернионы и пространственное вращение и Оператор вращения (векторное пространство)

Слово "спряжение "помимо значения, указанного выше, также может означать получение элемента а к г а р⁻¹ где р - некоторый ненулевой кватернион. Все элементы, которые сопряжены с данным элементом (в этом смысле слова сопряженные) имеют одинаковую действительную часть и одинаковую норму векторной части. (Таким образом, сопряжение в другом смысле является одним из сопряженных в этом смысле.)

Таким образом, мультипликативная группа ненулевых кватернионов действует сопряжением на копии ℝ³ состоящий из кватернионов, действительная часть которых равна нулю. Сопряжение единичного кватерниона (кватерниона абсолютного значения 1) с действительной частью cos (φ) поворот на угол 2φосью вращения является направление векторной части. Преимущества кватернионов:

• Избегая карданный замок, проблема с такими системами, как Углы Эйлера.
• Быстрее и компактнее, чем матрицы.
• Неособое представление (например, по сравнению с углами Эйлера).
• Пары единичных кватернионов представляют собой вращение в 4D пространство (см. Вращения в четырехмерном евклидовом пространстве: алгебра четырехмерных вращений ).

Множество всех кватернионов единиц (версоры ) образует 3-сфера S³ и группа (а Группа Ли ) при умножении, двойное покрытие группа ТАК (3, ℝ) действительных ортогональных 3 × 3матрицы из детерминант 1 с два единичные кватернионы соответствуют каждому вращению при указанном выше соответствии. Увидеть трюк с тарелкой.

Дальнейшая информация: Группы точек в трех измерениях

Образ подгруппы версоров - это точечная группа, и наоборот, прообраз точечной группы является подгруппой версоров. Прообраз конечной точечной группы называется тем же именем с префиксом двоичный. Например, прообраз группа икосаэдров это бинарная группа икосаэдра.

Группа версоров изоморфна SU (2), группа сложных унитарный 2 × 2 матрицы детерминант  1.

Позволять А - набор кватернионов вида а + б я + c j + d k где а, б, в, и d либо все целые числа или все полуцелые числа. Набор А это кольцо (на самом деле домен ) и решетка и называется кольцом Кватернионы Гурвица. В этом кольце 24 единичных кватерниона, и они являются вершинами обычный 24 ячейки с участием Символ Шлефли {3,4,3}. Они соответствуют двойному покрытию вращательной группы симметрии регулярного тетраэдр. Аналогично, вершины обычный 600 ячеек с символом Шлефли {3,3,5}  можно принять за единицу икозианцы, соответствующее двойному покрытию группы вращательной симметрии правильный икосаэдр. Двойное покрытие вращательной группы симметрии регулярного октаэдр соответствует кватернионам, которые представляют вершины дисфеноидальный 288-элементный.

Кватернионные алгебры

Основная статья: Кватернионная алгебра

Кватернионы можно обобщить на другие алгебры, называемые кватернионные алгебры. Взять F быть любым поле с характеристикой отличной от 2, и а и б быть элементами F; четырехмерный унитарный ассоциативная алгебра можно определить над F с основанием 1, я, j, и я j, где я² = а, j² = б и я j = −j i (так (я j)² = −а б).

Алгебры кватернионов изоморфны алгебре 2 × 2матрицы над F или форма алгебры с делением над F, в зависимости от выбора а и б.

Кватернионы как четная часть Cl_3,0(ℝ)

Основная статья: Спинор § Трехмерный

Полезность кватернионов для геометрических вычислений может быть обобщена на другие измерения путем определения кватернионов как четной части. Cl⁺
_3,0(ℝ) из Алгебра Клиффорда Cl_3,0(ℝ). Это ассоциативная многовекторная алгебра, построенная из фундаментальных базисных элементов. σ₁, σ₂, σ₃ используя правила продукта

${\displaystyle \sigma _{1}^{2}=\sigma _{2}^{2}=\sigma _{3}^{2}=1,}$

${\displaystyle \sigma _{i}\sigma _{j}=-\sigma _{j}\sigma _{i}\qquad (j\neq i).}$

Если взять эти фундаментальные базисные элементы для представления векторов в трехмерном пространстве, то окажется, что отражение вектора р в плоскости, перпендикулярной единичному вектору ш можно написать:

${\displaystyle r^{\prime }=-w\,r\,w.}$

Два отражения совершают поворот на угол, вдвое превышающий угол между двумя плоскостями отражения, поэтому

${\displaystyle r^{\prime \prime }=\sigma _{2}\sigma _{1}\,r\,\sigma _{1}\sigma _{2}}$

соответствует повороту на 180 ° в плоскости, содержащей σ₁ и σ₂. Это очень похоже на соответствующую формулу кватерниона,

${\displaystyle r^{\prime \prime }=-\mathbf {k} \,r\,\mathbf {k} .}$

На самом деле они идентичны, если мы проведем идентификацию

${\displaystyle \mathbf {k} =\sigma _{2}\sigma _{1}\,,\quad \mathbf {i} =\sigma _{3}\sigma _{2}\,,\quad \mathbf {j} =\sigma _{1}\sigma _{3}\,,}$

и несложно подтвердить, что это сохраняет соотношения Гамильтона

${\displaystyle \mathbf {i} ^{2}=\mathbf {j} ^{2}=\mathbf {k} ^{2}=\mathbf {i\,j\,k} =-1~.}$

На этом рисунке так называемые "векторные кватернионы" (то есть чисто мнимые кватернионы) соответствуют не векторам, а бивекторы - величины с величиной и ориентацией, связанные с конкретным 2Dсамолеты а не 1Dнаправления. Отношение к сложные числа становится понятнее: в 2D, с двумя векторными направлениями σ₁ и σ₂, имеется только один базисный элемент бивектора σ₁σ₂, так что только одно воображаемое. Но в 3D с тремя векторными направлениями есть три базисных элемента бивектора. σ₁σ₂, σ₂σ₃, σ₃σ₁Итак, три воображаемых.

Это рассуждение распространяется дальше. В алгебре Клиффорда Cl_4,0(ℝ), имеется шесть бивекторных базисных элементов, так как с четырьмя разными направлениями базовых векторов можно определить шесть разных пар и, следовательно, шесть разных линейно независимых плоскостей. Вращения в таких пространствах с использованием этих обобщений кватернионов, называемых роторы, может быть очень полезно для приложений, связанных с однородные координаты. Но только в 3D количество базисных бивекторов равно количеству базисных векторов, и каждый бивектор может быть идентифицирован как псевдовектор.

Размещение кватернионов в этом более широком контексте дает несколько преимуществ:^[40]

• Роторы являются естественной частью геометрической алгебры и легко понимаются как кодирование двойного отражения.
• В геометрической алгебре ротор и объекты, на которые он действует, живут в одном пространстве. Это устраняет необходимость изменять представления и кодировать новые структуры данных и методы, что традиционно требуется при дополнении линейной алгебры кватернионами.
• Роторы универсально применимы к любому элементу алгебры, не только к векторам и другим кватернионам, но также к линиям, плоскостям, окружностям, сферам, лучам и так далее.
• в конформная модель В евклидовой геометрии роторы позволяют кодировать вращение, перемещение и масштабирование в одном элементе алгебры, универсально воздействуя на любой элемент. В частности, это означает, что роторы могут представлять вращение вокруг произвольной оси, тогда как кватернионы ограничены осью через начало координат.
• Преобразования, кодируемые ротором, делают интерполяцию особенно простой.
• Роторы естественным образом переносятся на Псевдоевклидовы пространства, например, Пространство Минковского из специальная теория относительности. В таких пространствах роторы могут использоваться для эффективного представления Лоренц усиливает, и интерпретировать формулы, содержащие гамма-матрицы.

Для получения дополнительной информации о геометрическом использовании алгебр Клиффорда см. Геометрическая алгебра.

Группа Брауэра

Дальнейшая информация: Группа Брауэра

Кватернионы "по сути" единственные (нетривиальные) центральная простая алгебра (CSA) над действительными числами, в том смысле, что каждое CSA над действительными числами является Эквивалент Брауэра к реалам или кватернионам. В явном виде Группа Брауэра вещественных чисел состоит из двух классов, представленных действительными числами и кватернионами, где группа Брауэра - это набор всех CSA, вплоть до отношения эквивалентности одного CSA, являющегося матричное кольцо над другим. Посредством Теорема Артина – Веддерберна (в частности, часть Веддерберна), все CSA - это матричные алгебры над алгеброй с делением, и, таким образом, кватернионы являются единственной нетривиальной алгеброй с делением над вещественными числами.

CSA - кольца над полем, которые простые алгебры (не имеют нетривиальных двусторонних идеалов, как и в случае с полями), центром которых является в точности поле, являются некоммутативным аналогом поля расширения, и являются более ограничительными, чем обычные расширения колец. Тот факт, что кватернионы являются единственным нетривиальным CSA над вещественными числами (с точностью до эквивалентности), можно сравнить с тем фактом, что комплексные числа являются единственным нетривиальным расширением поля вещественных чисел.

Котировки

Я рассматриваю это как неэлегантность или несовершенство в кватернионах или, скорее, в том состоянии, в котором оно было до сих пор развернуто, всякий раз, когда становится или кажется необходимым прибегнуть к х, у, г, и т.п.

— Уильям Роуэн Гамильтон^[41]

Говорят, что время имеет только одно измерение, а пространство - три измерения. ... Математический кватернион состоит из обоих этих элементов; на техническом языке это можно назвать «время плюс пространство» или «пространство плюс время»: и в этом смысле он имеет или, по крайней мере, включает ссылку на четыре измерения. И как Один Времени, Три Пространства, Мог в Цепи Символов быть опоясанным..

— Уильям Роуэн Гамильтон^{[42][требуется полная цитата ]}

Кватернионы пришли от Гамильтона после того, как он проделал действительно хорошую работу; и, хотя они были прекрасны и изобретательны, они были несмешанным злом для тех, кто прикоснулся к ним каким-либо образом, включая Клерк Максвелл.

— У. Томпсон, лорд Кельвин (1892)^{[нужна цитата ]}

Позже я пришел к выводу, что в том, что касается векторного анализа, который мне требовался, кватернион не только не требовался, но и был положительным злом немалой величины; и что благодаря его избеганию создание векторного анализа стало довольно простым и его работа также была упрощена, и что его можно было удобно согласовать с обычной декартовой работой.

— Оливер Хевисайд (1893)^[43]

Ни матрицы, ни кватернионы, ни обычные векторы не были исключены из этих десяти [дополнительных] глав. Ибо, несмотря на неоспоримую мощь современного тензорного исчисления, эти старые математические языки, на мой взгляд, продолжают давать заметные преимущества в ограниченной области специальной теории относительности. Более того, как в науке, так и в повседневной жизни, владение более чем одним языком также ценно, поскольку оно расширяет наши взгляды, способствует критике и предохраняет от ипостаси [слабого основания] этого вопрос, выраженный словами или математическими символами.

— Людвик Зильберштейн (1924)^{[44][требуется полная цитата ]}

... кватернионы, кажется, источают атмосферу упадка девятнадцатого века как довольно неудачный вид в борьбе за жизнь математических идей. По общему признанию, математики до сих пор хранят в своих сердцах теплое место из-за замечательных алгебраических свойств кватернионов, но, увы, такой энтузиазм мало что значит для упрямого физика.

— Саймон Л. Альтманн (1986)^[45]

Смотрите также

• 3-сфера
• Ассоциативная алгебра
• Бикватернион
• Алгебра Клиффорда
• Комплексное число
• Преобразование между кватернионами и углами Эйлера
• Алгебра деления
• Двойной кватернион
• Двойное комплексное число
• Углы Эйлера
• Внешняя алгебра
• Геометрическая алгебра
• Кватернион Гурвица
• Кватернионный порядок Гурвица
• Гиперболический кватернион
• Номер гиперкомплекса
• Ленарт сфера
• Октонион
• Матрицы Паули
• Группа Quaternion
• Кватернион переменная
• Кватернионная матрица
• Кватернионный многогранник
• Кватернионное проективное пространство
• Кватернионы и пространственное вращение
• Оператор вращения (векторное пространство)
• Вращения в 4-мерном евклидовом пространстве
• Slerp
• Сплит-кватернион
• Тессеракт

Заметки

1. Более личный взгляд на кватернионы был написан Иоахим Ламбек в 1995 году. Он написал в своем эссе Если бы Гамильтон победил: кватернионы в физике: «Мой собственный интерес как аспиранта был вызван вдохновляющей книгой Зильберштейна». В заключение он заявил: «Я твердо верю, что кватернионы могут стать коротким путем для чистых математиков, желающих ознакомиться с некоторыми аспектами теоретической физики». Ламбек, Дж. (1995). «Если бы Гамильтон победил: кватернионы в физике». Математика. Интеллигенсер. Vol. 17 нет. 4. С. 7–15. Дои:10.1007 / BF03024783.
2. Важно отметить, что векторная часть кватерниона на самом деле является «аксиальным» вектором илипсевдовектор ", не обычный или «полярный» вектор, как было формально доказано Альтманном (1986).^[26] Полярный вектор может быть представлен в вычислениях (например, для вращения с помощью кватернионного «преобразования подобия») чисто воображаемым кватернионом без потери информации, но эти два понятия не следует путать. Ось «двоичного» (180 °) кватерниона вращения в таком случае соответствует направлению представленного полярного вектора.
3. Для сравнения, реальные цифры (ℝ) имеют размерность 1, комплексные числа (ℂ) имеют размерность 2, а октонионы (${\displaystyle \mathbb {O} }$) иметь размер 8.
4. Определение квадратных корней из минус единицы в ℍ было дано Гамильтоном^[35] но часто опускался в других текстах. К 1971 году сфера была включена Сэмом Перлисом в его трехстраничную экспозицию, включенную в Исторические темы в алгебре (стр. 39) опубликовано Национальный совет учителей математики. Совсем недавно сфера квадратных корней из минус единицы описана в Ян Р. Портеус книга Алгебры Клиффорда и классические группы (Кембридж, 1995) в предложении 8.13 на стр. 60.
5. Книги по прикладной математике, такие как Корке (2017)^[38] часто используют разные обозначения с φ := 1/2θ - это, другая переменная θ = 2φ.

использованная литература

1. «О кватернионах; или о новой системе воображаемых в алгебре». Письмо Джону Т. Грейвсу. 17 октября 1843 г.
2. Розенфельд, Борис Абрамович (1988). История неевклидовой геометрии: эволюция концепции геометрического пространства. Springer. п. 385. ISBN  9780387964584.
3. Гамильтон. Ходжес и Смит. 1853. с.60. кватернион факторные линии трехмерное пространство время
4. Харди 1881. Джинн, Хит и др. 1881. с. 32. ISBN  9781429701860.
5. Кунце, Карстен; Шебен, Гельмут (ноябрь 2004 г.). «Распределение кватернионов Бингама и его сферическое преобразование радона в текстурном анализе». Математическая геология. 36 (8): 917–943. Дои:10.1023 / B: MATG.0000048799.56445.59. S2CID  55009081.
6. Смит, Фрэнк (Тони). "Почему не седенион?". Получено 8 июн 2018.
7. Увидеть Хазевинкель, Губарени и Кириченко 2004, п.12
8. Конвей и Смит 2003, п.9
9. Брэдли, Роберт Э .; Сандифер, Чарльз Эдвард (2007). Леонард Эйлер: жизнь, работа и наследие. п. 193. ISBN  978-0-444-52728-8.. Они упоминают Вильгельм Блашке заявление в 1959 г. о том, что «кватернионы были впервые идентифицированы Л. Эйлером в письме к Гольдбаху от 4 мая 1748 г.», и они комментируют, что «нет никакого смысла говорить, что Эйлер« идентифицировал »кватернионы в этом письме ... это утверждение абсурдно ".
10. Альтманн, Саймон Л. (декабрь 1989 г.). «Гамильтон, Родригес и скандал с кватернионом». Математический журнал. 62 (5): 306. Дои:10.2307/2689481. JSTOR  2689481.
11. Гаусс, К.Ф. (1900). «Mutationen des Raumes [Преобразования пространства] (ок. 1819 г.)». У Мартина Бренделя (ред.). Карл Фридрих Гаусс Верке [Работы Карла Фридриха Гаусса]. 8. статья отредактирована профессором Штекелем из Киля, Германия. Геттинген, Германия: Königlichen Gesellschaft der Wissenschaften [Королевское общество наук]. С. 357–361.
12. Гамильтон, W.R. (1844). "Письмо". Лондонский, Эдинбургский и Дублинский философский журнал и научный журнал. Vol. xxv. С. 489–495.
13. Гамильтон, сэр W.R. (1866). Гамильтон, W.E. (ред.). Элементы кватернионов. Лондон, Великобритания: Longmans, Green, & Co.
14. Шумейк, Кен (1985). «Анимация вращения с помощью кватернионных кривых» (PDF). Компьютерная графика. 19 (3): 245–254. Дои:10.1145/325165.325242. Представлено на СИГГРАФ '85.
15. Расхитительница гробниц (1996) часто называют первой компьютерной игрой для массового рынка, в которой кватернионы использовались для достижения плавного трехмерного вращения. См. Например Ник Бобик (июль 1998 г.). «Вращение объектов с помощью кватернионов». Разработчик игр.
16. Маккарти, Дж. М. (1990). Введение в теоретическую кинематику. MIT Press. ISBN  978-0-262-13252-7.
17. Шу, Цзянь-Цзюнь; Оу, Л.С. (2004). «Попарное выравнивание последовательности ДНК с использованием представления гиперкомплексного числа». Вестник математической биологии. 66 (5): 1423–1438. arXiv:1403.2658. Дои:10.1016 / j.bulm.2004.01.005. PMID  15294431. S2CID  27156563.
18. Шу, Цзянь-Цзюнь; Ли Ю. (2010). «Гиперкомплексная кросс-корреляция последовательностей ДНК». Журнал биологических систем. 18 (4): 711–725. arXiv:1402.5341. Дои:10.1142 / S0218339010003470. S2CID  5395916.
19. Гурвиц, А. (1919), Vorlesungen über die Zahlentheorie der Quaternionen, Берлин: J. Springer, JFM  47.0106.01, что касается Кватернионы Гурвица
20. Жирар, П. Р. (1984). «Группа кватернионов и современная физика». Европейский журнал физики. 5 (1): 25–32. Bibcode:1984EJPh .... 5 ... 25G. Дои:10.1088/0143-0807/5/1/007.
21. Жирар, Патрик Р. (1999). «Уравнения Эйнштейна и алгебра Клиффорда» (PDF). Успехи в прикладных алгебрах Клиффорда. 9 (2): 225–230. Дои:10.1007 / BF03042377. S2CID  122211720. Архивировано из оригинал (PDF) 17 декабря 2010 г.
22. Уэрта, Джон (27 сентября 2010 г.). "Представляем кватернионы" (PDF). В архиве (PDF) с оригинала от 21.10.2014. Получено 8 июн 2018.
23. Вуд, Чарли (6 сентября 2018 г.). «Странные числа, породившие современную алгебру». Блог абстракций. Журнал Quanta.
24. Канун (1976), п. 391)
25. «Математика - Преобразования с использованием кватернионов». Евклидово пространство. Ротация q1 с последующим вращением q2 эквивалентно одному повороту q2 q1. Обратите внимание на изменение порядка, то есть мы помещаем первое вращение в правую часть умножения.
26. Альтманн, С. Вращения, кватернионы и двойные группы. Гл. 12.
27. Гамильтон, сэр Уильям Роуэн (1866). «Статья 285». Элементы кватернионов. Longmans, Green, & Company. п.310.
28. Харди (1881). «Элементы кватернионов». Наука. library.cornell.edu. 2 (75): 65. Дои:10.1126 / science.os-2.75.564. PMID  17819877.
29. "группа кватернионов". Wolframalpha.com.
30. Гиббс, Дж. Уиллард; Уилсон, Эдвин Бидуэлл (1901). Векторный анализ. Издательство Йельского университета. п.428. правый тензор диадика
31. Гамильтон, W.R. (1844–1850). «О кватернионах или новой системе воображаемых в алгебре». Коллекция Дэвида Р. Уилкинса. Философский журнал. Тринити-колледж, Дублин.
32. «Визуализация кватернионов». Морган-Кауфманн / Эльзевир. 2005 г.
33. "[название не указано; определяющая оценка]". Wolframalpha.com.
34. Farebrother, Ричард Уильям; Грос, Юрген; Трошке, Свен-Оливер (2003). «Матричное представление кватернионов». Линейная алгебра и ее приложения. 362: 251–255. Дои:10.1016 / с0024-3795 (02) 00535-9.
35. Гамильтон, W.R. (1899). Элементы кватернионов (2-е изд.). п. 244. ISBN  1-108-00171-8.
36. "[название не указано]" (PDF). bridgesmathart.org. архив. Получено 19 августа 2018.
37. Сяркка, Симо (28 июня 2007 г.). «Заметки о кватернионах» (PDF). Lce.hut.fi. Архивировано из оригинал (PDF) 5 июля 2017 г.
38. Корк, Питер (2017). Робототехника, зрение и управление - фундаментальные алгоритмы в MATLAB®. Springer. ISBN  978-3-319-54413-7.
39. Парк, футбольный клуб; Равани, Бахрам (1997). «Плавная инвариантная интерполяция вращений». Транзакции ACM на графике. 16 (3): 277–295. Дои:10.1145/256157.256160. S2CID  6192031.
40. «Кватернионы и геометрическая алгебра». geometricalgebra.net. Получено 2008-09-12. Смотрите также: Дорст, Лео; Фонтийне, Даниэль; Манн, Стивен (2007). Геометрическая алгебра для компьютерных наук. Морган Кауфманн. ISBN  978-0-12-369465-2.
41. Цитата из письма Тейта Кэли.^{[нужна цитата ]}
42. Грейвс, Р. Жизнь сэра Уильяма Роуэна Гамильтона.
43. Хевисайд, Оливер (1893). Электромагнитная теория. я. Лондон, Великобритания: Издательская компания «Электрик». С. 134–135.
44. Людвик Зильберштейн (1924). Заметки о подготовке второго издания его Теория относительности.
45. Альтманн, Саймон Л. (1986). Вращения, кватернионы и двойные группы. Кларендон Пресс. ISBN  0-19-855372-2. LCCN  85013615.

Внешние статьи и ресурсы

Книги и публикации

• Гамильтон, Уильям Роуэн (1844). «О кватернионах, или о новой системе воображаемых в алгебре». Философский журнал. 25 (3): 489–495. Дои:10.1080/14786444408645047.*
• Гамильтон, Уильям Роуэн (1853), "Лекции по кватернионам ". Ирландская королевская академия.
• Гамильтон (1866) Элементы кватернионов Дублинский университет Нажмите. Отредактировал Уильям Эдвин Гамильтон, сын покойного автора.
• Гамильтон (1899) Элементы кватернионов том I, (1901) том II. Отредактировано Чарльз Джаспер Джоли; опубликовано Longmans, Green & Co..
• Тейт, Питер Гатри (1873), "Элементарный трактат о кватернионах". 2-е изд., Кембридж, [англ.]: The University Press.
• Максвелл, Джеймс Клерк (1873 г.) "Трактат об электричестве и магнетизме "Кларендон Пресс, Оксфорд.
• Тейт, Питер Гатри (1886), "«Архивная копия». Архивировано 8 августа 2014 года.. Получено 26 июня, 2005.". M.A. Sec. R.S.E. Британская энциклопедия, Девятое издание, 1886 г., т. XX, стр. 160–164. (сжатый PostScript файл)
• Джоли, Чарльз Джаспер (1905). Руководство кватернионов. Макмиллан. LCCN  05036137.
• Макфарлейн, Александр (1906). Векторный анализ и кватернионы (4-е изд.). Вайли. LCCN  16000048.
• Чисхолм, Хью, изд. (1911). "Алгебра". Британская энциклопедия (11-е изд.). Издательство Кембриджского университета. (См. Раздел о кватернионах.)
• Финкельштейн, Дэвид; Jauch, Josef M .; Шиминович, Самуэль; Speiser, Дэвид (1962). «Основы квантовой механики кватернионов». J. Math. Phys. 3 (2): 207–220. Дои:10.1063/1.1703794.
• Дю Валь, Патрик (1964). Гомографии, кватернионы и вращения. Оксфордские математические монографии. Кларендон Пресс. LCCN  64056979.
• Кроу, Майкл Дж. (1967), История векторного анализа: Эволюция идеи векторной системы, Университет Нотр-Дам Пресс. Обзор основных и второстепенных векторных систем 19-го века (Гамильтон, Мёбиус, Беллавитис, Клиффорд, Грассманн, Тейт, Пирс, Максвелл, Макфарлейн, Маколи, Гиббс, Хевисайд).
• Альтманн, Саймон Л. (1989). «Гамильтон, Родригес и скандал с кватернионом». Математический журнал. 62 (5): 291–308. Дои:10.1080 / 0025570X.1989.11977459.
• Адлер, Стивен Л. (1995). Кватернионная квантовая механика и квантовые поля. Международная серия монографий по физике. 88. Издательство Оксфордского университета. ISBN  0-19-506643-X. LCCN  94006306.
• Трифонов, Владимир (1995). «Линейное решение проблемы четырехмерности». Письма Еврофизики. 32 (8): 621–6. arXiv:физика / 0301044. Дои:10.1209/0295-5075/32/8/001. S2CID  5057819.
• Уорд, Дж. П. (1997). Кватернионы и числа Кэли: алгебра и приложения. Kluwer Academic. ISBN  0-7923-4513-4.
• Кантор, И.Л .; Солодников, А. (1989). Гиперкомплексные числа, элементарное введение в алгебры. Springer-Verlag. ISBN  0-387-96980-2.
• Гюрлебек, Клаус; Sprössig, Вольфганг (1997). Кватернионное исчисление и исчисление Клиффорда для физиков и инженеров. Математические методы на практике. 1. Вайли. ISBN  0-471-96200-7. LCCN  98169958.
• Койперс, Джек (2002). Кватернионы и последовательности вращения: учебник по применению к орбитам, аэрокосмической отрасли и виртуальной реальности. Princeton University Press. ISBN  0-691-10298-8.
• Конвей, Джон Хортон; Смит, Дерек А. (2003). О кватернионах и октонионах: их геометрия, арифметика и симметрия. А.К. Питерс. ISBN  1-56881-134-9. (обзор ).
• Джек, П. (2003). «Физическое пространство как кватернионная структура, I: уравнения Максвелла. Краткое примечание». arXiv:math-ph / 0307038.
• Кравченко Владислав (2003). Прикладной кватернионный анализ. Heldermann Verlag. ISBN  3-88538-228-8.
• Хазевинкель, Михиэль; Губарени, Надия; Кириченко, Владимир В. (2004). Алгебры, кольца и модули. 1. Springer. ISBN  1-4020-2690-0.
• Хэнсон, Эндрю Дж. (2006). Визуализация кватернионов. Эльзевир. ISBN  0-12-088400-3.
• Трифонов, Владимир (2007). «Естественная геометрия ненулевых кватернионов». Международный журнал теоретической физики. 46 (2): 251–7. arXiv:math-ph / 0606007. Дои:10.1007 / s10773-006-9234-9. S2CID  121363018. Архивировано из оригинал на 2011-08-05.
• Бинц, Эрнст; Стручки, Соня (2008). «1. Тело кватернионов». Геометрия групп Гейзенберга.. Американское математическое общество. ISBN  978-0-8218-4495-3.
• Доран, Крис Дж. Л.; Ласенби, Энтони Н. (2003). Геометрическая алгебра для физиков. Издательство Кембриджского университета. ISBN  978-0-521-48022-2.
• Винс, Джон А. (2008). Геометрическая алгебра для компьютерной графики. Springer. ISBN  978-1-84628-996-5.
• Для молекул, которые можно рассматривать как классические твердые тела молекулярная динамика компьютерное моделирование использует кватернионы. Впервые они были введены для этой цели Эванс, Д.Дж. (1977). «О представлении ориентационного пространства». Мол. Phys. 34 (2): 317–325. Дои:10.1080/00268977700101751.
• Чжан, Фучжэнь (1997). «Кватернионы и матрицы кватернионов». Линейная алгебра и ее приложения. 251: 21–57. Дои:10.1016/0024-3795(95)00543-9.
• Рон Голдман (2010). Переосмысление кватернионов: теория и вычисления. Морган и Клейпул. ISBN  978-1-60845-420-4.
• Евс, Ховард (1976), Введение в историю математики (4-е изд.), Нью-Йорк: Холт, Райнхарт и Уинстон, ISBN  0-03-089539-1

Ссылки и монографии

• "Уведомления Quaternion". Уведомления и материалы, относящиеся к презентациям на конференции Quaternion
• «Кватернион», Энциклопедия математики, EMS Press, 2001 [1994]
• "Часто задаваемые вопросы". Матрица и кватернион. 1.21.
• Sweetser, Дуг. «Занимаемся физикой с кватернионами».
• Кватернионы для компьютерной графики и механики (Гернот Хоффман)
• Гспонер, Андре; Хурни, Жан-Пьер (2002). "Физическое наследие сэра У. Р. Гамильтона". arXiv:math-ph / 0201058.
• Уилкинс, Д. «Исследования Гамильтона кватернионов».
• Гроссман, Дэвид Дж. "Quaternion Julia Fractals".] Кватернион с трехмерной трассировкой лучей Юлия Фракталс
• «Кватернионная математика и преобразования». Отличная страница, объясняющая основы математики со ссылками на простые формулы преобразования вращения.
• Мэтьюз, Джон Х. «Библиография кватернионов». Архивировано из оригинал 02 сентября 2006 г.
• "Кватернионные силы". GameDev.net.
• Хэнсон, Эндрю. "Визуализация домашней страницы Quaternions". Архивировано из оригинал на 2006-11-05.
• Карни, Чарльз Ф.Ф. (Январь 2007 г.). «Кватернионы в молекулярном моделировании». J. Mol. График. Мод. 25 (5): 595–604. arXiv:физика / 0506177. Дои:10.1016 / j.jmgm.2006.04.002. PMID  16777449. S2CID  6690718.
• Мебиус, Йохан Э. (2005). «Матричное доказательство теоремы о представлении кватернионов для четырехмерных вращений». arXiv:математика / 0501249.
• Мебиус, Йохан Э. (2007). «Вывод формулы Эйлера – Родригеса для трехмерных вращений из общей формулы для четырехмерных вращений». arXiv:математика / 0701759.
• "Гамильтон-Уолк". Кафедра математики, NUI Maynooth.
• «Использование кватернионов для представления вращения». OpenGL: Учебники. Архивировано из оригинал на 2007-12-15.
• Дэвид Эриксон, Министерство оборонных исследований и разработок Канады (DRDC), Полный вывод матрицы вращения из представления унитарного кватерниона в статье DRDC TR 2005-228.
• Мартинес, Альберто. «Отрицательная математика, как математические правила могут быть изменены». Исторический факультет Техасского университета. Архивировано из оригинал на 24.09.2011.
• Штальке, Д. «Кватернионы в классической механике» (PDF).
• Морье-Жену, Софи; Овсиенко, Валентин (2008). «Ну что, папа, тройняшек умножить можно?». arXiv:0810.5562 [math.AC ]. описывает, как кватернионы могут быть преобразованы в косо-коммутативную алгебру, градуируемую Z/2 × Z/2 × Z/2.
• Джойс, Хелен (ноябрь 2004 г.). "Любопытные кватернионы". организовано Джон Баэз.
• Ибанез, Луис. "Учебник по кватернионам. Часть I" (PDF). Архивировано из оригинал (PDF) на 2012-02-04. Получено 2011-12-05. Часть II (PDF; используя терминологию Гамильтона, которая отличается от современной)
• Ghiloni, R .; Моретти, В .; Перотти, А. (2013). «Непрерывное срезное функциональное исчисление в кватернионных гильбертовых пространствах». Rev. Math. Phys. 25 (4): 1350006–126. arXiv:1207.0666. Bibcode:2013RvMaP..2550006G. Дои:10.1142 / S0129055X13500062. S2CID  119651315.
  Ghiloni, R .; Моретти, В .; Перотти, А. (2017). «Спектральные представления нормальных операторов с помощью переплетающихся кватернионных проекционно-значимых мер». Rev. Math. Phys. 29: 1750034. arXiv:1602.02661. Дои:10.1142 / S0129055X17500349. две пояснительные статьи о непрерывном функциональном исчислении и спектральной теории в квантернионных гильбертовых пространствах, полезных в строгой кватернионной квантовой механике.
• Кватернионы приложение Android показывает кватернион, соответствующий ориентации устройства.
• Вращение объектов с использованием кватернионов статья, в которой говорится об использовании Quaternions для вращения в видеоиграх / компьютерной графике.