Иррациональный номер - Irrational number - Wikipedia
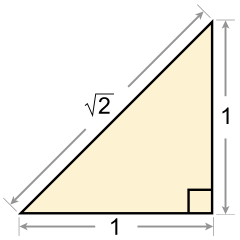
В математика, то иррациональные числа все действительные числа которые не рациональное число. То есть иррациональные числа нельзя выразить как отношение двух целые числа. Когда соотношение длины двух отрезков является иррациональным числом, отрезки также описываются как несоизмеримый, что означает, что у них нет общей «меры», то есть не существует длины («меры»), какой бы короткой она ни была, которую можно было бы использовать для выражения длин обоих из двух данных сегментов как целых кратных сам.
Среди иррациональных чисел есть соотношение π длины окружности к ее диаметру, число Эйлера е, золотое сечение φ, а квадратный корень из двух[1][2][3]. Фактически, все квадратные корни из натуральные числа, кроме идеальные квадраты, иррациональны.
Как и все действительные числа, иррациональные числа могут быть выражены в позиционная запись, особенно как десятичное число. В случае иррациональных чисел десятичное разложение не прекращается, и заканчиваться повторяющейся последовательностью. Например, десятичное представление π начинается с 3,14159, но конечное количество цифр не может представлять π точно, и не повторяется. И наоборот, завершающее или повторяющееся десятичное раскрытие должно быть рациональным числом. Это доказуемые свойства рациональных чисел и позиционных систем счисления, которые не используются в качестве определений в математике.
Иррациональные числа также можно выразить как непрерывные непрерывные дроби и многие другие способы.
Как следствие Доказательство Кантора что настоящие числа бесчисленный и рациональные счетно, отсюда следует, что почти все реальные числа иррациональны.[4]
История

Древняя Греция
Первое доказательство существования иррациональных чисел обычно приписывают Пифагорейский (возможно Гиппас из Метапонта ),[5] кто, вероятно, обнаружил их, определяя стороны пентаграмма.[6]Существовавший тогда метод Пифагора должен был утверждать, что должна быть какая-то достаточно маленькая неделимая единица, которая могла бы равномерно вписаться в одну из этих длин, а также в другую. Однако Гиппас в V веке до нашей эры смог сделать вывод, что на самом деле не существовало общей единицы измерения, и что утверждение о таком существовании на самом деле было противоречием. Он сделал это, продемонстрировав, что если гипотенуза из равнобедренный прямоугольный треугольник действительно был соизмеримый с ногой, то одна из этих длин, измеренная в этой единице измерения, должна быть как нечетной, так и четной, что невозможно. Его рассуждения таковы:
- Начните с равнобедренного прямоугольного треугольника со сторонами целых чисел. а, б, и c. Отношение гипотенузы к катету представлено как c:б.
- Предполагать а, б, и c в минимально возможных сроках (т.е. у них нет общих факторов).
- Посредством теорема Пифагора: c2 = а2+б2 = б2+б2 = 2б2. (Поскольку треугольник равнобедренный, а = б).
- С c2 = 2б2, c2 делится на 2, а значит, даже.
- С c2 даже, c должно быть даже.
- С c четный, делящий c на 2 дает целое число. Позволять у быть этим целым числом (c = 2у).
- Квадрат с обеих сторон c = 2у дает c2 = (2у)2, или же c2 = 4у2.
- Подставляя 4у2 за c2 в первом уравнении (c2 = 2б2) дает нам 4у2= 2б2.
- Деление на 2 дает 2у2 = б2.
- С у целое число, а 2у2 = б2, б2 делится на 2, а значит, даже.
- С б2 даже, б должно быть даже.
- Мы только что показали, что оба б и c должно быть даже. Следовательно, у них есть общий множитель 2. Однако это противоречит предположению, что у них нет общих множителей. Это противоречие доказывает, что c и б не могут одновременно быть целыми числами, и, следовательно, существование числа, которое не может быть выражено как отношение двух целых чисел.[7]
Греческие математики назвал это соотношение несоизмеримых величин алогос, или невыразимо. Гиппаса, однако, не хвалили за его усилия: согласно одной легенде, он сделал свое открытие, находясь в море, и впоследствии был выброшен за борт своими товарищами-пифагорейцами, «… за то, что создал во вселенной элемент, который отрицал… доктрину о том, что все явления во Вселенной можно свести к целым числам и их отношениям ».[8] Другая легенда гласит, что Гиппас был просто изгнан за это откровение. Какими бы ни были последствия для самого Гиппаса, его открытие представляло собой очень серьезную проблему для пифагорейской математики, поскольку оно разрушило предположение о неразрывности числа и геометрии - основу их теории.
Открытие несоизмеримых соотношений указывало на еще одну проблему, с которой столкнулись греки: отношение дискретного к непрерывному. Это было обнаружено Зенон Элейский, который поставил под сомнение концепцию, согласно которой количества дискретны и состоят из конечного числа единиц заданного размера. Согласно прежним греческим концепциям, они обязательно должны быть такими, поскольку «целые числа представляют собой отдельные объекты, а соизмеримое соотношение представляет собой отношение между двумя наборами дискретных объектов»,[9] но Зенон обнаружил, что на самом деле «[количества] в целом не являются дискретным набором единиц; вот почему появляются отношения несоизмеримых [величин]… Другими словами, [количества] непрерывны ».[9] Это означает, что вопреки популярной концепции времени не может быть неделимой мельчайшей единицы измерения для любой величины. Фактически, эти количественные единицы обязательно должны быть бесконечный. Например, рассмотрим линейный сегмент: этот сегмент можно разделить пополам, половину - пополам, половину - пополам и так далее. Этот процесс может продолжаться бесконечно, потому что всегда остается разделить другую половину. Чем чаще сегмент делится вдвое, тем ближе единица измерения к нулю, но никогда не достигает точного нуля. Именно это и пытался доказать Зенон. Он попытался доказать это, сформулировав четыре парадокса, который продемонстрировал противоречия, присущие математической мысли того времени. Хотя парадоксы Зенона точно продемонстрировали недостатки современных математических концепций, они не рассматривались как доказательство альтернативы. В представлении греков опровержение обоснованности одной точки зрения не обязательно доказывало обоснованность другой, и поэтому требовалось дальнейшее исследование.
Следующий шаг сделали Евдокс Книдский, который формализовал новую теорию пропорции, которая учитывала как соизмеримые, так и несоизмеримые величины. Центральным в его идее было различие между величиной и числом. Величина «... не была числом, а обозначала такие объекты, как отрезки линий, углы, площади, объемы и время, которые могли изменяться, как мы бы сказали, непрерывно. Величины были противопоставлены числам, которые прыгали от одного значения к другому, от 4 до 5. "[10] Числа состоят из некоторой наименьшей, неделимой единицы, тогда как величины бесконечно уменьшаются. Поскольку никакие количественные значения не были присвоены величине, Евдокс смог учесть как соизмеримые, так и несоизмеримые отношения, определяя соотношение по величине и пропорции как равенство между двумя отношениями. Убрав количественные значения (числа) из уравнения, он избежал ловушки, связанной с необходимостью выражать иррациональное число в виде числа. «Теория Евдокса позволила греческим математикам добиться огромного прогресса в геометрии, предоставив необходимую логическую основу для несоизмеримых соотношений».[11] Эта несоизмеримость рассматривается в «Элементах» Евклида, книга X, предложение 9.
В результате различия между числом и величиной геометрия стала единственным методом, который мог учитывать несоизмеримые отношения. Поскольку предыдущие числовые основы все еще были несовместимы с концепцией несоизмеримости, греческий акцент сместился с таких числовых концепций, как алгебра, и сосредоточился почти исключительно на геометрии. Фактически, во многих случаях алгебраические концепции были переформулированы в геометрические термины. Это может объяснить, почему мы все еще понимаем Икс2 и Икс3 в качестве Икс в квадрате и Икс куб вместо Икс во вторую степень и Икс в третью степень. Также критически важным для работы Зенона с несоизмеримыми величинами был фундаментальный акцент на дедуктивном мышлении, который явился результатом фундаментального разрушения ранней греческой математики. Осознание того, что некоторые основные концепции существующей теории расходятся с реальностью, потребовало полного и тщательного исследования аксиом и предположений, лежащих в основе этой теории. Исходя из этой необходимости, Евдокс разработал метод истощения, типа сокращение до абсурда что «... установило дедуктивную организацию на основе явных аксиом ...», а также «... подкрепило ранее принятое решение полагаться на дедуктивное рассуждение для доказательства».[12] Этот метод исчерпания - первый шаг в создании исчисления.
Феодор из Кирены доказал иррациональность серпы целых чисел до 17, но остановился на этом, вероятно, потому, что алгебра, которую он использовал, не могла быть применена к квадратному корню из 17.[13]
Он не был до тех пор Евдокс разработал теорию пропорции, которая учитывала иррациональные, а также рациональные соотношения, что позволило создать прочную математическую основу иррациональных чисел.[14]
Индия
Геометрические и математические проблемы, связанные с иррациональными числами, такими как квадратные корни, были решены очень рано во время Ведический период в Индии. Ссылки на такие расчеты есть в Самхиты, Брахманы, а Шульба Сутры (800 г. до н.э. или ранее). (См. Bag, Indian Journal of History of Science, 25 (1-4), 1990).
Предполагается, что концепция иррациональности была неявно принята Индийские математики с 7 века до нашей эры, когда Манава (ок. 750 - 690 до н. э.) считали, что квадратные корни чисел, таких как 2 и 61, не могут быть точно определены.[15] Однако историк Карл Бенджамин Бойер пишет, что «подобные утверждения малообоснованны и маловероятны».[16]
Также предлагается, чтобы Арьябхата (V век нашей эры) при вычислении значения числа пи до 5 значащих цифр использовали слово асанна (приближение), означающее, что это не только приближение, но и несоизмеримость (или иррациональность) значения.
Позже в своих трактатах индийские математики писали об арифметике сурдов, включая сложение, вычитание, умножение, рационализацию, а также разделение и извлечение квадратных корней.[17]
Математикам нравится Брахмагупта (в 628 г.) и Бхаскара I (629 г. н.э.) внесли свой вклад в эту область, как и другие последовавшие за ней математики. В 12 веке Бхаскара II оценили некоторые из этих формул и подвергли их критике, выявив их ограничения.
В течение 14-16 веков Мадхава Сангамаграмы и Керальская школа астрономии и математики обнаружил бесконечная серия для нескольких иррациональных чисел, таких как π и некоторые иррациональные значения тригонометрические функции. Джиешхадева предоставил доказательства для этих бесконечных серий в Юктибхана.[18]
Средний возраст
в Средний возраст, развитие алгебра к Мусульманские математики разрешил иррациональные числа рассматриваться как алгебраические объекты.[19] Математики Ближнего Востока также объединили концепции "номер " и "величина "в более общее представление о действительные числа критиковал идею Евклида о соотношения, разработал теорию составных отношений и расширил понятие числа до отношений непрерывной величины.[20] В своем комментарии к книге 10 Элементы, то Персидский математик Аль-Махани (ум. 874/884) осмотрены и классифицированы квадратичные иррациональные числа и кубические иррациональные числа. Он дал определения рациональных и иррациональных величин, которые он рассматривал как иррациональные числа. Он свободно разбирался с ними, но объясняет их геометрическими терминами следующим образом:[21]
«Это будет рациональным (величина), когда мы, например, скажем 10, 12, 3%, 6% и т. Д., Потому что его значение произносится и выражается количественно. То, что нерационально, является иррациональным, и его невозможно произнести и представить его значение количественно. Например: корни чисел, таких как 10, 15, 20, которые не являются квадратами, стороны чисел, которые не являются кубами. и Т. Д."
В отличие от евклидова концепции величин как линий, Аль-Махани рассматривал целые числа и дроби как рациональные величины, а квадратные корни и кубические корни как иррациональные величины. Он также представил арифметический подход к концепции иррациональности, поскольку он относит к иррациональным величинам следующее:[21]
«их суммы или различия, или результаты их прибавления к рациональной величине, или результаты вычитания такой величины из иррациональной, или рациональной величины из нее».
В Египтянин математик Абу Камил Шуджа ибн Аслам (ок. 850 - 930) был первым, кто принял иррациональные числа как решения квадратные уравнения или как коэффициенты в уравнение, часто в виде квадратных корней, кубических корней и четвертые корни.[22] В 10 веке Иракский математик Аль-Хашими предоставил общие доказательства (а не геометрические демонстрации) для иррациональных чисел, поскольку он рассматривал умножение, деление и другие арифметические функции.[23] Иранский математик, Абу Джафар аль-Хазин (900–971) дает определение рациональных и иррациональных величин, утверждая, что если определенная количество является:[24]
"содержится в определенной заданной величине один или несколько раз, тогда эта (данная) величина соответствует рациональному числу ... Каждый раз, когда эта (последняя) величина составляет половину, треть или четверть данной величины (единицы) или, по сравнению с (единицей), составляет три, пять или три пятых, это рациональная величина. И, в общем, каждая величина, которая соответствует этой величине (т.е. к единице), как одно число к другому, рационально. Если же величина не может быть представлена в виде кратного числа, то часть (1 /п) или части (м/п) данной величины, это иррационально, т.е. это не может быть выражено иначе, как через корни ».
Многие из этих концепций были в конечном итоге приняты европейскими математиками спустя некоторое время после Латинские переводы XII века. Аль-Хассар, марокканский математик из Фес специализируясь на Исламское наследство юриспруденции в 12 веке впервые упоминается использование дробной черты, где числители и знаменатели разделены горизонтальной чертой. В своем обсуждении он пишет: «... например, если вам говорят написать три пятых и одну треть пятого, напишите так: ."[25] Это же дробное обозначение вскоре появляется в работах Леонардо Фибоначчи в 13 веке.[26]
Современный период
17 век увидел мнимые числа стать мощным инструментом в руках Авраам де Муавр, и особенно Леонард Эйлер. Завершение теории сложные числа в 19 веке повлекло за собой разделение иррациональных чисел на алгебраические и трансцендентные числа, доказательство существования трансцендентных чисел и возрождение научных исследований теории иррациональных чисел, в значительной степени игнорируемых с тех пор, как Евклид. В 1872 году были опубликованы теории Карл Вейерштрасс (его ученик Эрнст Коссак), Эдуард Гейне (Журнал Крелля, 74), Георг Кантор (Аннален, 5), и Ричард Дедекинд. В 1869 году Мере взял ту же отправную точку, что и Гейне, но теория обычно относится к 1872 году. Метод Вейерштрасса полностью изложен Сальваторе Пинчерле в 1880 г.,[27] и Дедекинда получили дополнительную известность благодаря более поздней работе автора (1888 г.) и одобрению Пол Таннери (1894 г.). Вейерштрасс, Кантор и Гейне основывают свои теории на бесконечных рядах, в то время как Дедекинд основывает свои теории на идее вырезать (Шнитт) в системе всех рациональное число, разделив их на две группы, обладающие определенными характерными свойствами. Этот предмет получил более поздние работы от Вейерштрасса, Леопольд Кронекер (Crelle, 101), и Шарль Мере.
Непрерывные дроби, тесно связанные с иррациональными числами (и благодаря Катальди, 1613 г.), привлекли внимание Эйлера и в начале XIX века получили известность благодаря трудам Жозеф-Луи Лагранж. Дирихле также внес свой вклад в общую теорию, как и многие участники, внесшие вклад в приложения этого предмета.
Иоганн Генрих Ламберт доказал (1761), что π не может быть рациональным и что еп иррационально, если п рационально (если только п = 0).[28] Хотя доказательство Ламберта часто называют неполным, современные оценки подтверждают его как удовлетворительное, и в действительности для своего времени оно необычайно строгое. Адриан-Мари Лежандр (1794), после введения Функция Бесселя – Клиффорда, предоставили доказательство того, что π2 иррационально, откуда сразу следует, что π также иррационально. Существование трансцендентные числа был впервые установлен Лиувиллем (1844, 1851). Потом, Георг Кантор (1873) доказали их существование другой метод, который показал, что каждый интервал в вещественных числах содержит трансцендентные числа. Чарльз Эрмит (1873) впервые доказано е трансцендентный, и Фердинанд фон Линдеманн (1882), исходя из выводов Эрмита, показал то же самое для π. Доказательство Линдеманна было значительно упрощено Вейерштрассом (1885 г.), а еще дальше - Дэвид Гильберт (1893), и, наконец, был сделан элементарным Адольф Гурвиц[нужна цитата ] и Пол Гордан.[29]
Примеры
Квадратные корни
В квадратный корень из 2 было первым числом, которое оказалось иррациональным, и эта статья содержит ряд доказательств. В Золотое сечение - еще одно известное квадратичное иррациональное число. Квадратные корни из всех натуральных чисел, не являющихся идеальные квадраты иррациональны, и доказательство можно найти в квадратичные иррациональные числа.
Общие корни
Приведенное выше доказательство для квадратного корня из двух можно обобщить, используя основная теорема арифметики. Это утверждает, что каждое целое число имеет уникальная факторизация в простые числа. Используя его, мы можем показать, что если рациональное число не является целым числом, то его целая степень не может быть целым числом, как в самые низкие сроки должен быть основной в знаменателе, который не делится на числитель, в какую бы степень они ни возводились. Следовательно, если целое число не является точным k-я степень другого целого числа, затем это первое целое число kй корень иррационально.
Логарифмы
Возможно, числа, которые легче всего доказать иррациональными, несомненно логарифмы. Вот доказательство от противного этот журнал2 3 иррационально (журнал2 3 ≈ 1.58 > 0).
Предположим журнал2 3 рационально. Для некоторых положительных целых чисел м и п, у нас есть
Следует, что
Однако число 2, возведенное в любую положительную целую степень, должно быть четным (потому что оно делится на 2), а число 3, возведенное в любую положительную целую степень, должно быть нечетным (так как ни одно из его главные факторы будет 2). Ясно, что целое число не может быть одновременно четным и нечетным: приходим к противоречию. Мы сделали единственное предположение, что журнал2 3 является рациональным (и поэтому выражается как частное целых чисел м/п с п ≠ 0). Противоречие означает, что это предположение должно быть ложным, т.е. log2 3 иррационально и никогда не может быть выражено как частное от целых чисел м/п с п ≠ 0.
Такие случаи, как журнал10 2 можно рассматривать аналогично.
Типы
- Теоретико-числовое различие: трансцендентный / алгебраический
- нормальный / ненормальный (ненормальный)
Трансцендентный / алгебраический
Почти все иррациональные числа трансцендентный и все реальные трансцендентные числа иррациональны (существуют также комплексные трансцендентные числа): в статье о трансцендентных числах приводится несколько примеров. Так е р и π р иррациональны для всех ненулевых рациональныхр, и, например, еπ тоже иррационально.
Иррациональные числа также можно найти в счетный набор реальных алгебраические числа (по существу определяется как реальный корни из многочлены с целыми коэффициентами), т.е. как действительные решения полиномиальных уравнений
где коэффициенты целые числа и . Любой рациональный корень этого полиномиального уравнения должно иметь вид р /s, куда р это делитель из а0 и s является делителем ап. Если настоящий рут полинома не входит в число этих конечных возможностей, это должно быть иррациональное алгебраическое число. Примерное доказательство существования таких алгебраических иррациональных чисел состоит в том, чтобы показать, что Икс0 = (21/2 + 1)1/3 является иррациональным корнем многочлена с целыми коэффициентами: он удовлетворяет (Икс3 − 1)2 = 2 и, следовательно, Икс6 − 2Икс3 - 1 = 0, и этот последний многочлен не имеет рациональных корней (единственными кандидатами для проверки являются ± 1, иИкс0, будучи больше 1, не является ни одним из них), поэтомуИкс0 - иррациональное алгебраическое число.
Поскольку алгебраические числа образуют подполе Из действительных чисел многие иррациональные действительные числа могут быть построены путем комбинирования трансцендентных и алгебраических чисел. Например, 3π + 2, π + √2 и е√3 иррациональны (и даже трансцендентны).
Десятичные разложения
Десятичное разложение иррационального числа никогда не повторяется и не заканчивается (последнее эквивалентно повторяющимся нулям), в отличие от любого рационального числа. То же верно и для двоичный, восьмеричный или же шестнадцатеричный расширений, и в целом для расширений в каждом позиционный обозначение с естественный базы.
Чтобы показать это, предположим, что мы делим целые числа п к м (куда м не равно нулю). Когда длинное деление применяется к разделению п к м, Только м остатки возможны. Если 0 появляется как остаток, десятичное раскрытие завершается. Если 0 никогда не встречается, алгоритм может работать не более м - 1 шаг без использования остатка более одного раза. После этого должен повториться остаток, а затем повторяется десятичное разложение.
И наоборот, предположим, что мы столкнулись с повторяющаяся десятичная дробь, мы можем доказать, что это дробь двух целых чисел. Например, рассмотрим:
Здесь повторяется 162, а длина повторения равна 3. Сначала мы умножаем на соответствующую степень 10, чтобы переместить десятичную запятую вправо так, чтобы она находилась прямо перед повторением. В этом примере мы умножим на 10, чтобы получить:
Теперь умножим это уравнение на 10.р куда р длина повтора. Это приводит к перемещению десятичной точки перед «следующим» повторением. В нашем примере умножаем на 103:
Результат двух умножений дает два разных выражения с точно такой же «десятичной частью», то есть хвостовой частью 10 000А соответствует концу 10А точно. Здесь и 10000А и 10А имеют .162162162... после десятичной точки.
Следовательно, когда мы вычитаем 10А уравнение из 10 000А уравнение, конец 10А аннулирует хвост из 10,000А оставив нас с:
потом
представляет собой отношение целых чисел и, следовательно, рациональное число.
Иррациональные силы
Дов Джарден дал простой не-конструктивное доказательство что существуют два иррациональных числа а и б, так что аб рационально:[30]
Учитывать √2√2; если это рационально, то возьмем а = б = √2. В противном случае возьмите а быть иррациональным числом √2√2 и б = √2. потом аб = (√2√2)√2 = √2√2·√2 = √22 = 2, что рационально.
Хотя приведенный выше аргумент не делает выбор между двумя случаями, Теорема Гельфонда – Шнайдера показывает, что √2√2 является трансцендентный, следовательно, иррационально. Эта теорема утверждает, что если а и б оба алгебраические числа, и а не равно 0 или 1, и б не является рациональным числом, то любое значение аб - трансцендентное число (может быть больше одного значения, если возведение в степень комплексного числа используется).
Пример, обеспечивающий простое конструктивное доказательство:[31]
База левой части иррациональна, а правая - рациональна, поэтому нужно доказать, что показатель в левой части, , иррационально. Это потому, что по формуле, связывающей логарифмы с разными основаниями,
что мы можем предположить, ради установления противоречие, равняется отношению м / п натуральных чисел. потом следовательно следовательно следовательно , которая является противоречивой парой простых факторизаций и, следовательно, нарушает основная теорема арифметики (уникальное разложение на простые множители).
Более сильный результат следующий:[32] Каждое рациональное число в интервале можно записать как аа для какого-то иррационального числа а или как пп для некоторого натурального числа п. По аналогии,[32] каждое положительное рациональное число можно записать как для какого-то иррационального числа а или как для некоторого натурального числа п.
Открытые вопросы
Неизвестно, если (или же ) иррационально. На самом деле не существует пары ненулевых целых чисел для которого известно, иррационально. Более того, неизвестно, если множество является алгебраически независимый над .
Неизвестно, если Каталонская постоянная, или Константа Эйлера – Маскерони иррациональны.[33][34][35] Неизвестно, есть ли тетрации или же рационально для некоторого целого числа [нужна цитата ]
Набор всех иррациональных
Поскольку реалы образуют бесчисленный множество, рациональными числами которого являются счетный подмножество дополнительных наборов иррациональных чисел неисчислимо.
Под обычным (Евклидово ) функция расстояния d (Икс, у) = |Икс − у|, действительные числа - это метрическое пространство а значит, и топологическое пространство. Ограничение функции евклидова расстояния придает иррациональным числам структуру метрического пространства. Поскольку подпространство иррациональных чисел не замкнуто, индуцированная метрика не является полный. Однако, будучи G-дельта набор - т.е. счетное пересечение открытых подмножеств - в полном метрическом пространстве пространство иррациональных чисел полностью метризуемый: то есть существует метрика на иррациональных числах, порождающая ту же топологию, что и ограничение евклидовой метрики, но относительно которой иррациональные числа полны. Это можно увидеть, не зная вышеупомянутого факта о множествах G-дельта: непрерывная дробь расширение иррационального числа определяет гомеоморфизм из пространства иррациональных чисел в пространство всех последовательностей натуральных чисел, которое, как легко видеть, полностью метризуемо.
Более того, множество всех иррациональных чисел является несвязным метризуемым пространством. Фактически иррациональные элементы, снабженные топологией подпространства, имеют основу Clopen наборы так что пространство нульмерно.
Смотрите также
- Число Брьюно
- Вычислимое число
- Диофантово приближение
- Доказательство того, что е иррационально
- Доказательство того, что π иррационально
- Корень квадратный из 3
- Корень квадратный из 5
- Тригонометрическое число
Рекомендации
- ^ 15 самых известных трансцендентных чисел. к Клиффорд А. Пиковер. URL получен 24 октября 2007 г.
- ^ http://www.mathsisfun.com/irrational-numbers.html; URL получен 24 октября 2007 г.
- ^ Вайсштейн, Эрик В. "Иррациональный номер". MathWorld. URL получен 26 октября 2007 г.
- ^ Кантор, Георг (1955) [1915]. Филип Журден (ред.). Вклад в основание теории трансфинитных чисел. Нью-Йорк: Дувр. ISBN 978-0-486-60045-1.
- ^ Курт фон Фриц (1945). «Открытие несоизмеримости Гиппасом из Метапонта». Анналы математики.CS1 maint: ref = harv (связь)
- ^ Джеймс Р. Чойк (1980). «Пентаграмма и открытие иррационального числа». Двухлетний математический журнал колледжа.CS1 maint: ref = harv (связь).
- ^ Клайн, М. (1990). Математическая мысль от древних до наших дней, Vol. 1. Нью-Йорк: Издательство Оксфордского университета. (Оригинальная работа опубликована в 1972 г.). стр.33.
- ^ Клайн 1990, стр. 32.
- ^ а б Клайн 1990, стр.34.
- ^ Клайн 1990, стр.48.
- ^ Клайн 1990, стр.49.
- ^ Клайн 1990, стр.50.
- ^ Роберт Л. Маккейб (1976). «Доказательства иррациональности Теодора». Математический журнал.CS1 maint: ref = harv (связь).
- ^ Чарльз Х. Эдвардс (1982). Историческое развитие математического анализа. Springer.
- ^ T. K. Puttaswamy, "Достижения древнеиндийских математиков", стр. 411–2, в Селин, Хелайн; Д'Амброзио, Убиратан, ред. (2000). Математика в разных культурах: история незападной математики. Springer. ISBN 1-4020-0260-2.CS1 maint: ref = harv (связь).
- ^ Boyer (1991). «Китай и Индия». История математики (2-е изд.). п. 208. ISBN 0471093742. OCLC 414892.
Утверждалось также, что первое признание несоизмеримого появляется в Индии во время Сульбасутра период, но такие утверждения недостаточно обоснованы. Аргументы в пользу раннего индуистского осознания несоизмеримых величин крайне маловероятны из-за отсутствия свидетельств того, что индийские математики того периода вплотную подошли к фундаментальным концепциям.
- ^ Датта, Бибхутибхусан; Сингх, Авадхеш Нараян (1993). "Surds в индуистской математике" (PDF). Индийский журнал истории науки. 28 (3): 253–264. Архивировано из оригинал (PDF) на 2018-10-03. Получено 18 сентября 2018.
- ^ Кац, В. Дж. (1995), "Идеи исчисления в исламе и Индии", Математический журнал (Математическая ассоциация Америки) 68 (3): 163–74.
- ^ О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф., "Арабская математика: забытый талант?", Архив истории математики MacTutor, Сент-Эндрюсский университет..
- ^ Матвиевская, Галина (1987). "Теория квадратичных иррациональных чисел в средневековой восточной математике". Летопись Нью-Йоркской академии наук. 500: 253–277 [254]. Дои:10.1111 / j.1749-6632.1987.tb37206.x.CS1 maint: ref = harv (связь).
- ^ а б Матвиевская, Галина (1987). "Теория квадратичных иррациональных чисел в средневековой восточной математике". Летопись Нью-Йоркской академии наук. 500: 253–277 [259]. Дои:10.1111 / j.1749-6632.1987.tb37206.x.CS1 maint: ref = harv (связь)
- ^ Жак Сезиано, "Исламская математика", стр. 148, дюйм Селин, Хелайн; Д'Амброзио, Убиратан (2000). Математика в разных культурах: история незападной математики. Springer. ISBN 1-4020-0260-2.CS1 maint: ref = harv (связь).
- ^ Матвиевская, Галина (1987). "Теория квадратичных иррациональных чисел в средневековой восточной математике". Летопись Нью-Йоркской академии наук. 500: 253–277 [260]. Дои:10.1111 / j.1749-6632.1987.tb37206.x.CS1 maint: ref = harv (связь).
- ^ Матвиевская, Галина (1987). "Теория квадратичных иррациональных чисел в средневековой восточной математике". Летопись Нью-Йоркской академии наук. 500: 253–277 [261]. Дои:10.1111 / j.1749-6632.1987.tb37206.x.CS1 maint: ref = harv (связь).
- ^ Кахори, Флориан (1928), История математических обозначений (Том 1), Ла Саль, Иллинойс: Издательская компания Open Court стр. 269.
- ^ (Кахори 1928, стр.89)
- ^ Сальваторе Пинчерле (1880). "Saggio di una Introduction alla teoria delle funzioni analitiche secondo i Principii del prof. C. Weierstrass". Giornale di Matematiche: 178–254,317–320.CS1 maint: ref = harv (связь)
- ^ Дж. Х. Ламберт (1761). "Mémoire sur quelques propriétés remarquables des Quantités transcendentes, circaires et logarithmiques" (PDF). Mémoires de l'Académie royale des Sciences de Berlin (на французском языке): 265–322. В архиве (PDF) из оригинала от 28 апреля 2016 г.CS1 maint: ref = harv (связь)
- ^ Гордан, Пол (1893). "Transcendenz von е унд π ". Mathematische Annalen. Тюбнер. 43 (2–3): 222–224. Дои:10.1007 / bf01443647.
- ^ Георгий, Александр; Веллеман, Дэниел Дж. (2002). Философия математики (PDF). Блэквелл. С. 3–4. ISBN 0-631-19544-0.
- ^ Лорд, Ник, "Математика кусается: иррациональные силы иррациональных чисел могут быть рациональными", Математический вестник 92, ноябрь 2008 г., стр. 534.
- ^ а б Маршалл, Эш Дж., И Тан, Йирен, "Рациональное число формы аа с а иррационально », Математический вестник 96, март 2012 г., стр. 106-109.
- ^ Вайсштейн, Эрик В. "Число Пи". MathWorld.
- ^ Вайсштейн, Эрик В. "Иррациональный номер". MathWorld.
- ^ Альберт, Джон. «Некоторые нерешенные проблемы теории чисел» (PDF). Отделение математики Университета Оклахомы. (Старший математический семинар, весенний курс 2008 г.)
дальнейшее чтение
- Адриан-Мари Лежандр, Éléments de Géometrie, Примечание IV, (1802 г.), Париж
- Рольф Валлиссер, «О доказательстве Ламбертом иррациональности числа π», в Алгебраическая теория чисел и диофантов анализ, Франц Хальтер-Кох и Роберт Ф. Тихи, (2000), Вальтер де Грюйер
внешняя ссылка
- Парадоксы Зенона и несоизмеримость (нет данных). Проверено 1 апреля 2008 г.
- Вайсштейн, Эрик В. "Иррациональный номер". MathWorld.













































